第一章 反比例函数综合素质评价试题(含解析)
文档属性
| 名称 | 第一章 反比例函数综合素质评价试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 11:30:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章综合素质评价
(120分 90分钟)
一、选择题(每题3分,共30分)
1.下列函数关系式中,y是x的反比例函数的是( )
2.若反比例函数 的图象经过点(2,-3),则它的图象也一定经过的点是( )
A.(-2,-3) B.(-3,-2) C.(1,-6) D.(6,1)
3.已知反比例函数 则下列描述正确的是( )
A.图象位于第一、三象限 B.图象必经过点
C.图象必经过点 D. y随x的增大而减小
4.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例函数关系.如图是该电路中电流 I与电阻R之间的函数关系的图象,当电阻R为5Ω时,电流I为( )
A.6 A B.5 A C.1.2 A D.1 A
5.如图,一次函数y=kx+b(k≠0)的图象与反比例函数 (m≠0)的图象交于点 A(-1,2),B(2,-1),则不等式 的解集是( )
A. x<-1或x>2 B.-1<x<0或0<x<2
C. x<-1或0<x<2 D.-1<x<0或x>2
6.如图是反比例函数 的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点 B,连接OA,则△AOB的面积是( )
A.1 B. C.2
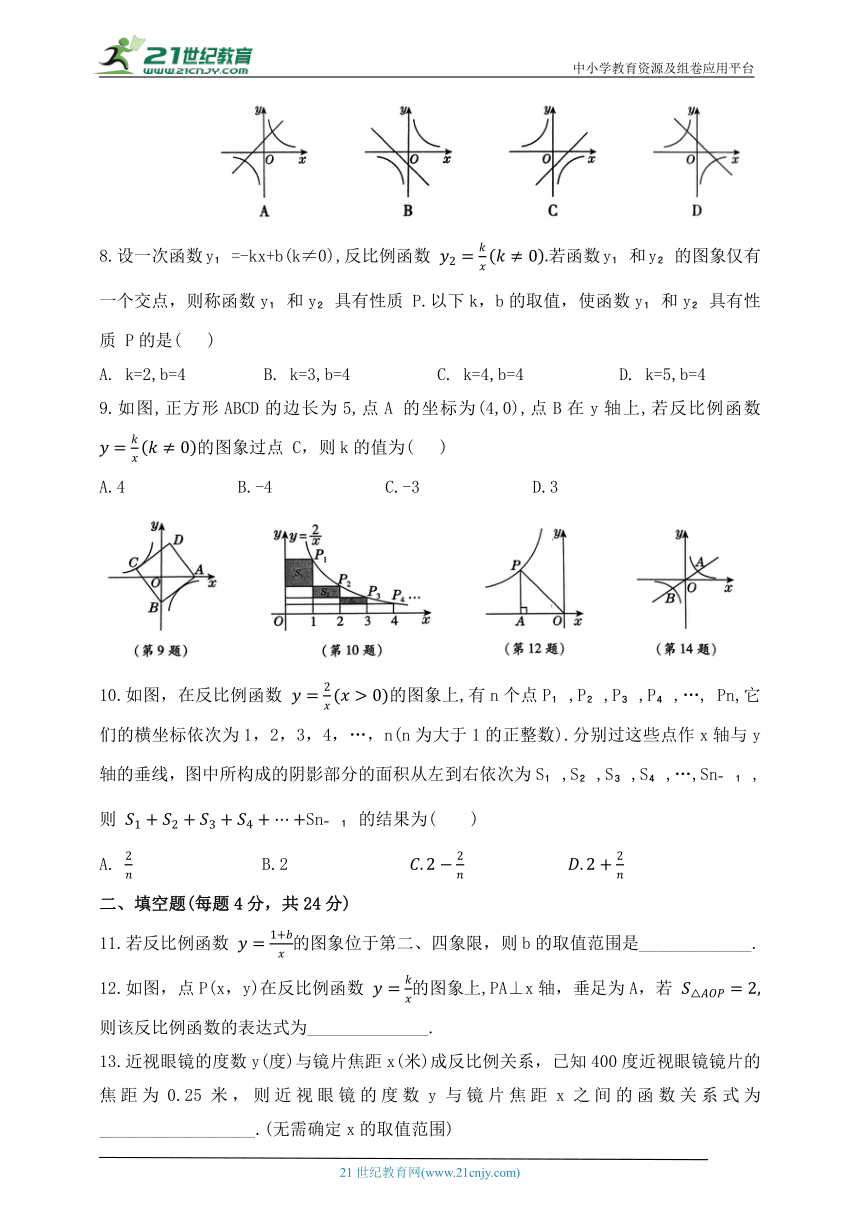
7.函数y=kx-k与 在同一坐标系中的图象可能是( )
8.设一次函数y =-kx+b(k≠0),反比例函数 若函数y 和y 的图象仅有一个交点,则称函数y 和y 具有性质 P.以下k,b的取值,使函数y 和y 具有性质 P的是( )
A. k=2,b=4 B. k=3,b=4 C. k=4,b=4 D. k=5,b=4
9.如图,正方形ABCD的边长为5,点A 的坐标为(4,0),点B在y轴上,若反比例函数 的图象过点 C,则k的值为( )
A.4 B.-4 C.-3 D.3
10.如图,在反比例函数 的图象上,有n个点P ,P ,P ,P ,…, Pn,它们的横坐标依次为1,2,3,4,…,n(n为大于1的正整数).分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S ,S ,S ,S ,…,Sn ,则 Sn 的结果为( )
A. B.2
二、填空题(每题4分,共24分)
11.若反比例函数 的图象位于第二、四象限,则b的取值范围是_____________.
12.如图,点P(x,y)在反比例函数 的图象上,PA⊥x轴,垂足为A,若 则该反比例函数的表达式为______________.
13.近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,已知400度近视眼镜镜片的焦距为0.25米,则近视眼镜的度数y与镜片焦距x之间的函数关系式为__________________.(无需确定x的取值范围)
14.如图,正比例函数.y=-k x和反比例函数 的图象相交于A,B两点,若点A的坐标是(3,2),则点B的坐标是_____________.
15.已知点A(a,y ),B(a+1,y )在反比例函数 (m是常数)的图象上,且y1<y2,.则a的取值范围是______________.
16.将一副三角板放置在如图所示的平面直角坐标系中,三角板顶点A与原点O重合,AB在x轴正半轴上,且. 点E在AD上, 将这副三角板整体向右平移____________个单位,C,E两点同时落在反比例函数 (k≠0,且x>0)的图象上.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分,共66分)
17.已知反比例函数
(1)若函数图象经过点A(-1,6),求m的值;
(2)若函数图象在第二、四象限,求m的取值范围;
(3)当x>0时,y随x的增大而减小,求m的取值范围.
18.在平面直角坐标系xOy中,直线y=x+b与双曲线 的一个交点为A(2,4),与y轴交于点 B.
(1)求m的值和点B的坐标;
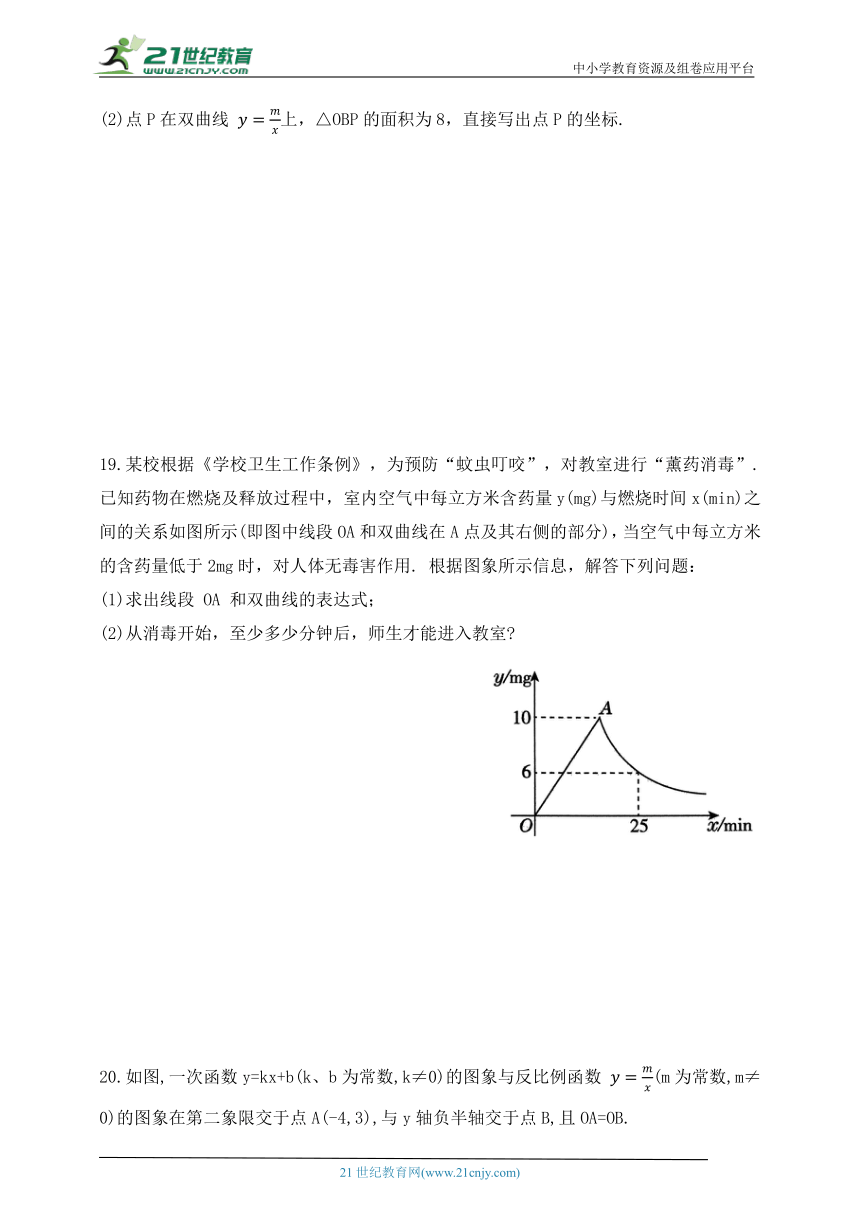
(2)点P在双曲线 上,△OBP的面积为8,直接写出点P的坐标.
19.某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(mg)与燃烧时间x(min)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2mg时,对人体无毒害作用. 根据图象所示信息,解答下列问题:
(1)求出线段 OA 和双曲线的表达式;
(2)从消毒开始,至少多少分钟后,师生才能进入教室
20.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数 (m为常数,m≠0)的图象在第二象限交于点A(-4,3),与y轴负半轴交于点B,且OA=OB.
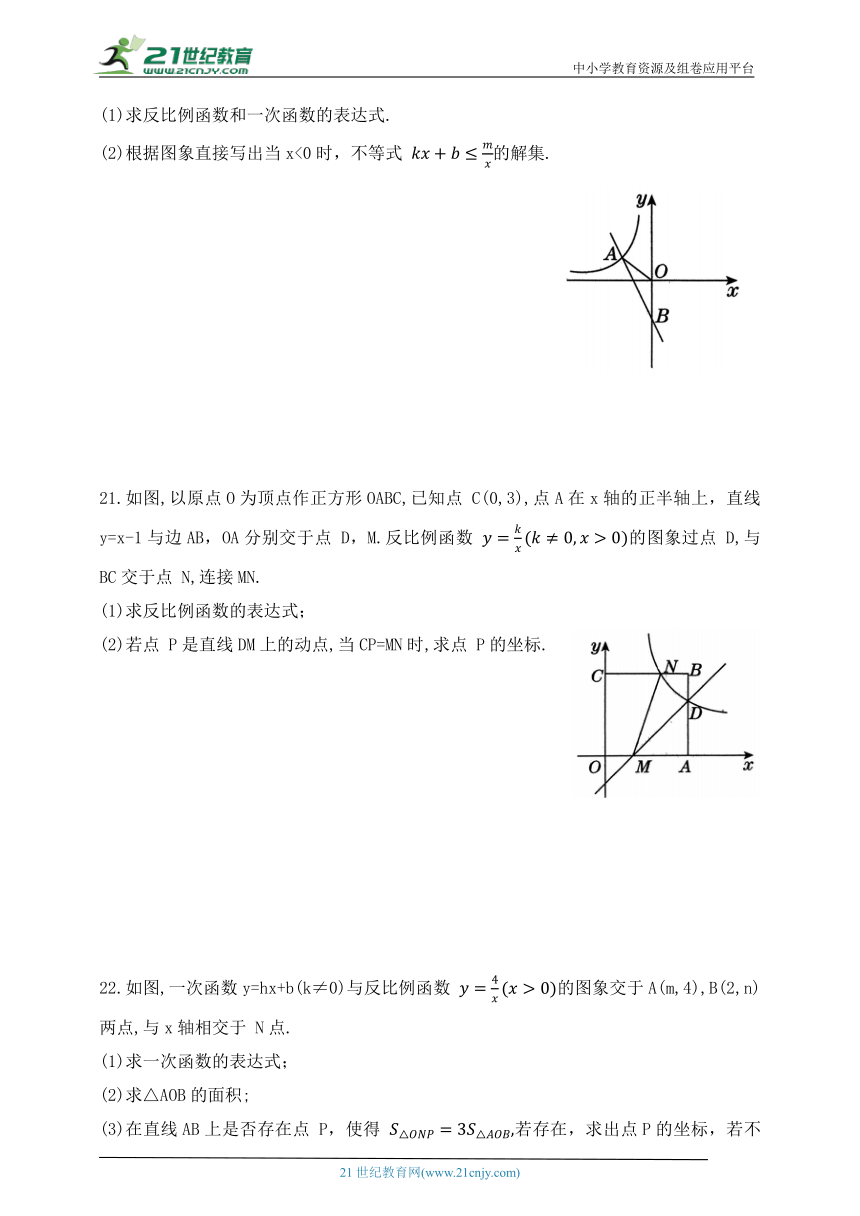
(1)求反比例函数和一次函数的表达式.
(2)根据图象直接写出当x<0时,不等式 的解集.
21.如图,以原点O为顶点作正方形OABC,已知点 C(0,3),点A在x轴的正半轴上,直线y=x-1与边AB,OA分别交于点 D,M.反比例函数 的图象过点 D,与BC交于点 N,连接MN.
(1)求反比例函数的表达式;
(2)若点 P是直线DM上的动点,当CP=MN时,求点 P的坐标.
22.如图,一次函数y=hx+b(k≠0)与反比例函数 的图象交于A(m,4),B(2,n)两点,与x轴相交于 N点.
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)在直线AB上是否存在点 P,使得 若存在,求出点P的坐标,若不存在,请说明理由.
参考答案
一、1. C 【点拨】根据反比例函数的定义,反比例函数的一般式是 即可判定各函数的类型是否符合题意.
2. C【点拨】因为反比例函数 的图象经过点(2,-3),所以k=2×(-3)=-6.分别计算选项中各点的横纵坐标之积,根据反比例函数图象上点的坐标特征判断,只有1×(-6)=-6.故选C.
3. C 【点拨】 中k=-6<0,∴函数的图象在第二、四象限,在每个象限内,y随x的增大而增大,故选项A、D不符合题意;当x=4时, 函数图象经过点 不过点 故选项B不符合题意,选项C符合题意.故选C.
4. C 【点拨】设 则 U=3×2=6,所以当R=5Ω时,I=1.2 A.故选C.
5. D 【点拨】由函数图象可知,当一次函数y=kx+b(k≠0)的图象在反比例函数 的图象下方时,x的取值范围是-12,∴不等式. 的解集是-12.故选 D.
6. B 【点拨】∵A的坐标为(x,y),∴OB=x,AB=y.
∵A为反比例函数 的图象上一点,∴xy=1, 故选B.
7. C 【点拨】当 k>0时,一次函数y=kx-k的图象过第一、三、四象限,反比例函数 的图象在第二、四象限;当k<0时,一次函数y=kx-k的图象过第一、二、四象限,反比例函数 的图象在第一、三象限.∴A、B、D不符合题意,C符合题意.故选C.
8. A 【点拨】整理方程 得.-kx +bx-k=0.
∵两函数图象只有一个交点,∴一元二次方程判别式为0,即b -4k =0.故选 A.
9. C【点拨】如图,过点C作CE⊥y轴于E,在正方形AB-CD中,AB=BC,∠ABC=90°,∴∠ABO+∠CBE=90°.∵∠OAB+∠ABO=90°,∴∠OAB=∠CBE.
∵点A的坐标为(4,0),∴OA =4.∵AB=5,∴OB=
在△ABO和△BCE中 ∴△ABO≌△BCE,∴OA = BE =4,CE =OB=3,
∴OE=BE-OB=4-3=1,∴点C的坐标为(-3,1).
∵反比例函数 的图象过点 C,∴k=xy=-3×1= -3.故选C.
10. C 【点拨】如图,由 得. 2,易知 故选 C.
二、11. b<-1【点拨】根据反比例函数 的性质k>0,图象位于第一、三象限;k<0,图象位于第二、四象限,可知1+b<0,∴b<-1.
【点拨】∵点P(x,y)在反比例函数 的图象上,PA⊥x轴,∴xy=k,OA = -x,PA =y. 即-xy = 4,∴xy=-4,∴k= -4.∴该反比例函数的表达式为
【点拨】设 由于(0.25,400)满足此函数表达式
14.(-3,-2) 【点拨】∵正比例函数与反比例函数的图象均关于原点对称,∴A、B两点关于原点对称.∵点A 的坐标为(3,2),∴点 B的坐标为(-3,-2).
15.-1<a<0 【点拨】∵m +1>0,.∴反比例函数y= (m是常数)的图象在第一、三象限,在每个象限内,y随x的增大而减小.①当点A(a,y ),B(a+1,y )在同一象限时,∵y <y ,∴a>a+1,此不等式无解,∴此种情况不符合题意,舍去;
②当点A(a,y ),B(a +1,y )在不同象限时,∵y <y ,∴点A在第三象限,点 B在第一象限,∴a<0,a+1>0,解得-1<a<0.综上所述,a的取值范围是-1<a<0.
【点拨】过点 E作EN⊥DB于点N,过点C作CM⊥BD于点 M,则∠DNE = ∠CMB=90°.在Rt△ABD中,∵ 8 ,∴DB=12.∵△BCD是等腰直角三角形,∴CM=∠DBA =90°,∴EN∥AB,∴易得△DEN∽△DAB, ∴点E的横坐标为 3 ,纵坐标为12-3=9.∴E(3 ,9).设将这副三角板整体向右平移m个单位,C,E两点同时落在反比例函数 且x>0)的图象上,则平移后 C,E两点的对应点分别为
解得 m=
三、17.【解】(1)∵函数图象经过点A(-1,6),∴m-8=xy= -1×6=-6,∴m=2.
(2)∵函数图象在第二、四象限,∴m-8<0,解得m<8.∴m的取值范围是m<8.
(3)∵当x>0时,y随x的增大而减小,∴m-8>0,解得m>8.∴m的取值范围是m>8.
18.【解】(1)∵双曲线 经过点A(2,4),∴m=8.
∵直线y=x+b经过点A(2,4),∴b=2.∴此直线与y轴的交点B的坐标为(0,2).
(2)点P的坐标为(8,1)或(-8,-1).
【点拨】(2)设△OBP的边OB边上的高为x,根据三角形的面积可得 从而可得点P的横坐标;再代入反比例函数的表达式可得点P的纵坐标,即可得点P的坐标.
19.【解】(1)设双曲线的表达式为 将(25,6)代入上式,得k=25×6=150.
∴双曲线的表达式为
将y=10代入 得 解得x=15,∴A(15,10).
设直线OA的表达式为y=nx,将A(15,10)的坐标代入上式,得
∴线段OA的表达式为 双曲线的表达式为
(2)将y=2代入 得 解得x=75.
答:从消毒开始,至少75 min后,师生才能进入教室.
20.【解】(1)把A(-4,3)的坐标代入 得m=-4×3=-12,∴反比例函数的表达式为 ∵OA=OB,∴OB=5,∴B(O,-5).
把A(-4,3),B(0,-5)的坐标分别代入y=kx+b,得 解得
∴一次函数的表达式为y=-2x-5.
(2)当x<0时,不等式 的解集为-4≤x<0.
21.【解】(1)∵C(0,3),∴OC=3.
∵四边形OABC是正方形,∴OA=OC=3.
∵M、D在直线y=x-1上,∴M(1,0),D(3,2).
∵D在 的图象上,∴k=6,
∴反比例函数的表达式为
(2)设P(a,a-1).
对于 当y=3时,x=2,∴N(2,3).
∵M(1,0),∴MN =(2-1) +3 =10.
∵CP=MN,∴CP =MN ,∴a +(a-1-3) =10,整理得,(a -4a+3=0,解得a =1,a =3.
∴P(1,0)或(3,2).
22.【解】(1)∵点A 在反比例函数 的图象上,
解得m=1,∴点A的坐标为(1,4).
∵点B在反比例函数 的图象上, 解得n=2.∴点 B的坐标为(2,2).
∵点A、B在y=kx+b的图象上, 解得
∴一次函数的表达式为y=-2x+6.
(2)直线 y=-2x+6与x轴的交点为N,∴点N的坐标为(3,0).
(3)存在.设P(x,y).
由(2)知 则
∴|y|=6,∴y=6或y=-6.
将y=6代入y=-2x+6中,得(6=-2x+6,解得x=0.
将y=-6代入y=-2x+6中,得-6=-2x+6,解得x=6.
故点 P的坐标为(0,6)或(6,-6).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章综合素质评价
(120分 90分钟)
一、选择题(每题3分,共30分)
1.下列函数关系式中,y是x的反比例函数的是( )
2.若反比例函数 的图象经过点(2,-3),则它的图象也一定经过的点是( )
A.(-2,-3) B.(-3,-2) C.(1,-6) D.(6,1)
3.已知反比例函数 则下列描述正确的是( )
A.图象位于第一、三象限 B.图象必经过点
C.图象必经过点 D. y随x的增大而减小
4.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例函数关系.如图是该电路中电流 I与电阻R之间的函数关系的图象,当电阻R为5Ω时,电流I为( )
A.6 A B.5 A C.1.2 A D.1 A
5.如图,一次函数y=kx+b(k≠0)的图象与反比例函数 (m≠0)的图象交于点 A(-1,2),B(2,-1),则不等式 的解集是( )
A. x<-1或x>2 B.-1<x<0或0<x<2
C. x<-1或0<x<2 D.-1<x<0或x>2
6.如图是反比例函数 的图象,点A(x,y)是反比例函数图象上任意一点,过点A作AB⊥x轴于点 B,连接OA,则△AOB的面积是( )
A.1 B. C.2
7.函数y=kx-k与 在同一坐标系中的图象可能是( )
8.设一次函数y =-kx+b(k≠0),反比例函数 若函数y 和y 的图象仅有一个交点,则称函数y 和y 具有性质 P.以下k,b的取值,使函数y 和y 具有性质 P的是( )
A. k=2,b=4 B. k=3,b=4 C. k=4,b=4 D. k=5,b=4
9.如图,正方形ABCD的边长为5,点A 的坐标为(4,0),点B在y轴上,若反比例函数 的图象过点 C,则k的值为( )
A.4 B.-4 C.-3 D.3
10.如图,在反比例函数 的图象上,有n个点P ,P ,P ,P ,…, Pn,它们的横坐标依次为1,2,3,4,…,n(n为大于1的正整数).分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S ,S ,S ,S ,…,Sn ,则 Sn 的结果为( )
A. B.2
二、填空题(每题4分,共24分)
11.若反比例函数 的图象位于第二、四象限,则b的取值范围是_____________.
12.如图,点P(x,y)在反比例函数 的图象上,PA⊥x轴,垂足为A,若 则该反比例函数的表达式为______________.
13.近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,已知400度近视眼镜镜片的焦距为0.25米,则近视眼镜的度数y与镜片焦距x之间的函数关系式为__________________.(无需确定x的取值范围)
14.如图,正比例函数.y=-k x和反比例函数 的图象相交于A,B两点,若点A的坐标是(3,2),则点B的坐标是_____________.
15.已知点A(a,y ),B(a+1,y )在反比例函数 (m是常数)的图象上,且y1<y2,.则a的取值范围是______________.
16.将一副三角板放置在如图所示的平面直角坐标系中,三角板顶点A与原点O重合,AB在x轴正半轴上,且. 点E在AD上, 将这副三角板整体向右平移____________个单位,C,E两点同时落在反比例函数 (k≠0,且x>0)的图象上.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分,共66分)
17.已知反比例函数
(1)若函数图象经过点A(-1,6),求m的值;
(2)若函数图象在第二、四象限,求m的取值范围;
(3)当x>0时,y随x的增大而减小,求m的取值范围.
18.在平面直角坐标系xOy中,直线y=x+b与双曲线 的一个交点为A(2,4),与y轴交于点 B.
(1)求m的值和点B的坐标;
(2)点P在双曲线 上,△OBP的面积为8,直接写出点P的坐标.
19.某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(mg)与燃烧时间x(min)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2mg时,对人体无毒害作用. 根据图象所示信息,解答下列问题:
(1)求出线段 OA 和双曲线的表达式;
(2)从消毒开始,至少多少分钟后,师生才能进入教室
20.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与反比例函数 (m为常数,m≠0)的图象在第二象限交于点A(-4,3),与y轴负半轴交于点B,且OA=OB.
(1)求反比例函数和一次函数的表达式.
(2)根据图象直接写出当x<0时,不等式 的解集.
21.如图,以原点O为顶点作正方形OABC,已知点 C(0,3),点A在x轴的正半轴上,直线y=x-1与边AB,OA分别交于点 D,M.反比例函数 的图象过点 D,与BC交于点 N,连接MN.
(1)求反比例函数的表达式;
(2)若点 P是直线DM上的动点,当CP=MN时,求点 P的坐标.
22.如图,一次函数y=hx+b(k≠0)与反比例函数 的图象交于A(m,4),B(2,n)两点,与x轴相交于 N点.
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)在直线AB上是否存在点 P,使得 若存在,求出点P的坐标,若不存在,请说明理由.
参考答案
一、1. C 【点拨】根据反比例函数的定义,反比例函数的一般式是 即可判定各函数的类型是否符合题意.
2. C【点拨】因为反比例函数 的图象经过点(2,-3),所以k=2×(-3)=-6.分别计算选项中各点的横纵坐标之积,根据反比例函数图象上点的坐标特征判断,只有1×(-6)=-6.故选C.
3. C 【点拨】 中k=-6<0,∴函数的图象在第二、四象限,在每个象限内,y随x的增大而增大,故选项A、D不符合题意;当x=4时, 函数图象经过点 不过点 故选项B不符合题意,选项C符合题意.故选C.
4. C 【点拨】设 则 U=3×2=6,所以当R=5Ω时,I=1.2 A.故选C.
5. D 【点拨】由函数图象可知,当一次函数y=kx+b(k≠0)的图象在反比例函数 的图象下方时,x的取值范围是-1
6. B 【点拨】∵A的坐标为(x,y),∴OB=x,AB=y.
∵A为反比例函数 的图象上一点,∴xy=1, 故选B.
7. C 【点拨】当 k>0时,一次函数y=kx-k的图象过第一、三、四象限,反比例函数 的图象在第二、四象限;当k<0时,一次函数y=kx-k的图象过第一、二、四象限,反比例函数 的图象在第一、三象限.∴A、B、D不符合题意,C符合题意.故选C.
8. A 【点拨】整理方程 得.-kx +bx-k=0.
∵两函数图象只有一个交点,∴一元二次方程判别式为0,即b -4k =0.故选 A.
9. C【点拨】如图,过点C作CE⊥y轴于E,在正方形AB-CD中,AB=BC,∠ABC=90°,∴∠ABO+∠CBE=90°.∵∠OAB+∠ABO=90°,∴∠OAB=∠CBE.
∵点A的坐标为(4,0),∴OA =4.∵AB=5,∴OB=
在△ABO和△BCE中 ∴△ABO≌△BCE,∴OA = BE =4,CE =OB=3,
∴OE=BE-OB=4-3=1,∴点C的坐标为(-3,1).
∵反比例函数 的图象过点 C,∴k=xy=-3×1= -3.故选C.
10. C 【点拨】如图,由 得. 2,易知 故选 C.
二、11. b<-1【点拨】根据反比例函数 的性质k>0,图象位于第一、三象限;k<0,图象位于第二、四象限,可知1+b<0,∴b<-1.
【点拨】∵点P(x,y)在反比例函数 的图象上,PA⊥x轴,∴xy=k,OA = -x,PA =y. 即-xy = 4,∴xy=-4,∴k= -4.∴该反比例函数的表达式为
【点拨】设 由于(0.25,400)满足此函数表达式
14.(-3,-2) 【点拨】∵正比例函数与反比例函数的图象均关于原点对称,∴A、B两点关于原点对称.∵点A 的坐标为(3,2),∴点 B的坐标为(-3,-2).
15.-1<a<0 【点拨】∵m +1>0,.∴反比例函数y= (m是常数)的图象在第一、三象限,在每个象限内,y随x的增大而减小.①当点A(a,y ),B(a+1,y )在同一象限时,∵y <y ,∴a>a+1,此不等式无解,∴此种情况不符合题意,舍去;
②当点A(a,y ),B(a +1,y )在不同象限时,∵y <y ,∴点A在第三象限,点 B在第一象限,∴a<0,a+1>0,解得-1<a<0.综上所述,a的取值范围是-1<a<0.
【点拨】过点 E作EN⊥DB于点N,过点C作CM⊥BD于点 M,则∠DNE = ∠CMB=90°.在Rt△ABD中,∵ 8 ,∴DB=12.∵△BCD是等腰直角三角形,∴CM=∠DBA =90°,∴EN∥AB,∴易得△DEN∽△DAB, ∴点E的横坐标为 3 ,纵坐标为12-3=9.∴E(3 ,9).设将这副三角板整体向右平移m个单位,C,E两点同时落在反比例函数 且x>0)的图象上,则平移后 C,E两点的对应点分别为
解得 m=
三、17.【解】(1)∵函数图象经过点A(-1,6),∴m-8=xy= -1×6=-6,∴m=2.
(2)∵函数图象在第二、四象限,∴m-8<0,解得m<8.∴m的取值范围是m<8.
(3)∵当x>0时,y随x的增大而减小,∴m-8>0,解得m>8.∴m的取值范围是m>8.
18.【解】(1)∵双曲线 经过点A(2,4),∴m=8.
∵直线y=x+b经过点A(2,4),∴b=2.∴此直线与y轴的交点B的坐标为(0,2).
(2)点P的坐标为(8,1)或(-8,-1).
【点拨】(2)设△OBP的边OB边上的高为x,根据三角形的面积可得 从而可得点P的横坐标;再代入反比例函数的表达式可得点P的纵坐标,即可得点P的坐标.
19.【解】(1)设双曲线的表达式为 将(25,6)代入上式,得k=25×6=150.
∴双曲线的表达式为
将y=10代入 得 解得x=15,∴A(15,10).
设直线OA的表达式为y=nx,将A(15,10)的坐标代入上式,得
∴线段OA的表达式为 双曲线的表达式为
(2)将y=2代入 得 解得x=75.
答:从消毒开始,至少75 min后,师生才能进入教室.
20.【解】(1)把A(-4,3)的坐标代入 得m=-4×3=-12,∴反比例函数的表达式为 ∵OA=OB,∴OB=5,∴B(O,-5).
把A(-4,3),B(0,-5)的坐标分别代入y=kx+b,得 解得
∴一次函数的表达式为y=-2x-5.
(2)当x<0时,不等式 的解集为-4≤x<0.
21.【解】(1)∵C(0,3),∴OC=3.
∵四边形OABC是正方形,∴OA=OC=3.
∵M、D在直线y=x-1上,∴M(1,0),D(3,2).
∵D在 的图象上,∴k=6,
∴反比例函数的表达式为
(2)设P(a,a-1).
对于 当y=3时,x=2,∴N(2,3).
∵M(1,0),∴MN =(2-1) +3 =10.
∵CP=MN,∴CP =MN ,∴a +(a-1-3) =10,整理得,(a -4a+3=0,解得a =1,a =3.
∴P(1,0)或(3,2).
22.【解】(1)∵点A 在反比例函数 的图象上,
解得m=1,∴点A的坐标为(1,4).
∵点B在反比例函数 的图象上, 解得n=2.∴点 B的坐标为(2,2).
∵点A、B在y=kx+b的图象上, 解得
∴一次函数的表达式为y=-2x+6.
(2)直线 y=-2x+6与x轴的交点为N,∴点N的坐标为(3,0).
(3)存在.设P(x,y).
由(2)知 则
∴|y|=6,∴y=6或y=-6.
将y=6代入y=-2x+6中,得(6=-2x+6,解得x=0.
将y=-6代入y=-2x+6中,得-6=-2x+6,解得x=6.
故点 P的坐标为(0,6)或(6,-6).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
