人教版七年级数学上册第三章 一元一次方程:3.1.2等式的性质课件 27张PPT
文档属性
| 名称 | 人教版七年级数学上册第三章 一元一次方程:3.1.2等式的性质课件 27张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 570.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 08:42:08 | ||
图片预览







文档简介
(共27张PPT)
第三章 一元一次方程
3.1.2 等式的性质
教学目标:
【知识与技能】
(1)了解等式的概念和等式的两条性质.
(2)学会利用等式的两条性质解简单的一元一次方程.
【过程与方法】
利用天平进行实际操作,培养学生观察、分析、概括及逻辑思维能力,引导学生熟练地运用等式的性质解决问题.
【情感态度与价值观】
渗透“化归”的思想,增强主动探究的意识,发展合理的推理思维.
教学重难点:
1理解和运用等式的性质.
2利用等式的性质把简单的一元一次方程化成“x=a”的形式.
抽象能力 运算能力
模型观念 应用意识
1.(2022新课标)掌握等式的基本性质.
2.能利用等式的性质解一元一次方程.
知识点一:等式的性质
(1)等式的性质1:等式两边加(或减) (或式子),结果仍 ;
即:如果a=b,那么a±c= .
b±c
相等
同一个数
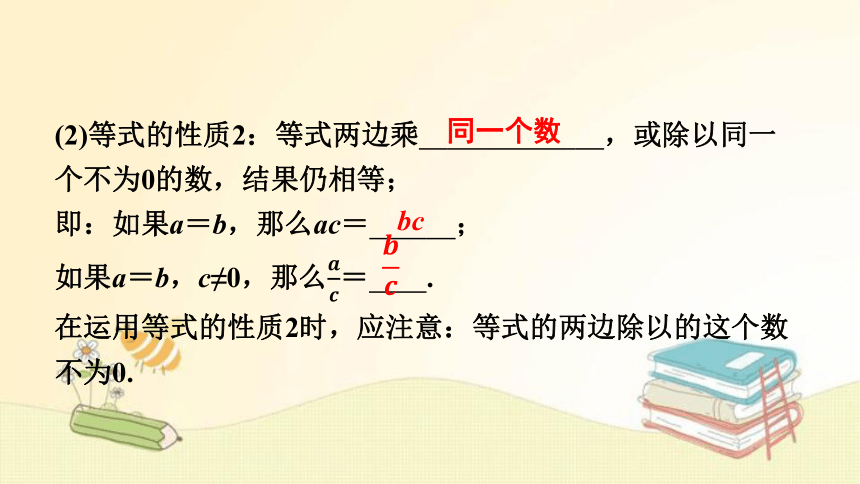
(2)等式的性质2:等式两边乘 ,或除以同一个不为0的数,结果仍相等;
即:如果a=b,那么ac= ;
如果a=b,c≠0,那么= .
在运用等式的性质2时,应注意:等式的两边除以的这个数不为0.
bc
同一个数
1.填空:
(1)在等式x+5=7的两边都 ,
得x=2,根据是 ;
(2)在等式x-3=8的两边都 ,
得x=11,根据是 ;
等式的性质1
加3
等式的性质1
减5
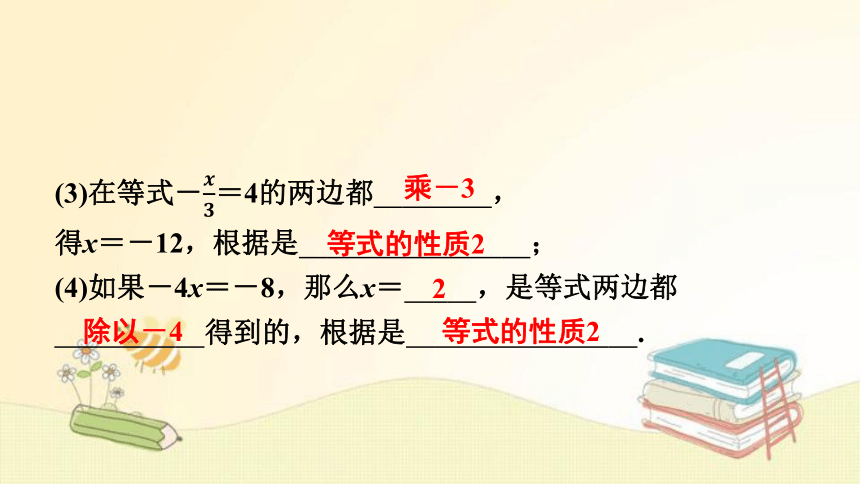
(3)在等式-=4的两边都 ,
得x=-12,根据是 ;
(4)如果-4x=-8,那么x= ,是等式两边都
得到的,根据是 .
等式的性质2
除以-4
2
等式的性质2
乘-3
知识点二:运用等式的性质解方程
利用等式的性质解方程的目的是将方程一步一步地变形为
x=a(常数)的形式,步骤如下:
(1)方程两边加(或减)同一个数(或式子),使一元一次方程左边是含 的项,右边是 项;
常数
未知数
(2)方程两边乘同一个数或除以同一个不为0的数,使未知数的 化为1,从而得出方程的解.
检验某数是不是某方程的解,方法是把这个数分别代入方程的左边和右边,注意“分别”看方程左、右两边的值是否
,若 ,则是方程的解;若 ,则不是.
不相等
相等
相等
系数
2.(北师7上P133)尝试运用等式的性质解一元一次方程.
(1)x+2=5.
解:方程的两边同时 ,
得 .
于是,x= .
反思:这道题应用了等式的性质 来解决.
1
3
x+2-2=5-2
减2
(2)-3x=15.
解:方程的两边同时 ,
得 .
于是,x= .
反思:这道题应用了等式的性质 来解决.
2
-5
-3x÷(-3)=15÷(-3)
除以-3
(3)3-x=9(并检验).
解:方程的两边同时减去 ,
得 .化简,得____________.
方程的两边同时乘 ,得x= .
检验:将 分别代入方程左右两边,左边= ,右边= ,因为 ,
所以 .
反思:这道题应用了等式的性质 与等式的性质 来解决.
-x=6
3-x-3=9-3
2
1
x=-18是原方程的解
左边=右边
9
9
x=-18
-18
-3
3
小结:利用等式的性质对等式进行变形时,等式两边要同时进行相同的运算,注意“0”不能作为除数和分母.
3.【例1】若a=b,下列各式不正确的是( )
A.a+9=b+9 B.-2a=-2b
C.a-7=b+7 D.
C
4.【例2】填空:
(1)已知等式x+3=-2,根据等式的性质1,两边
,得到x= ;
(2)已知等式x=6,根据等式的性质2,两边 ,得到x= ;
同时除以
9
-5
同时减去3
小结:等式的变形先要联想到等式的性质,再仔细观察、分析前后两个等式的结构有何变化,从而确定是应用哪条性质.
(3)已知等式6y=2y-4,根据等式的性质1,两边
,得到4y= ,再根据等式的性质2,两边 ,得到 .
y=-1
同时除以4
-4
同时减去2y
5.【例3】(人教7上P82、北师7上P133)利用等式的性质解下列方程并检验:
(1)x+7=26; (2)-5x=20;
(3)-x-5=4.
x=-4
x=-27
x=19
(检验略)
小结:利用等式的性质解方程,实质就是将方程一步步转化为x=a(a为常数)的形式.把x的值代入检验时,等号左右两边的值相等,否则x的值不是方程的解.
小结:先设未知数,再找出相等关系列方程.
6.【例4】列一元一次方程,不求解:
某超市销售有甲、乙两种商品,甲商品每件进价10元,乙商品每件进价30元.若该超市同时一次购进甲、乙两种商品共80件,恰好用去1 600元,能购进甲、乙两种商品各多少件?
.
解:设购进甲商品x件,得10x+30(80-x)=1 600.
7.下列等式的变形中,不正确的是( )
A.若x=y,则x+5=y+5
B.若(a≠0),则x=y
C.若-3x=-3y,则x=y
D.若mx=my,则x=y
D
8.填空:
(1)已知等式5m-3=6,
根据等式的性质 ,
两边同时 ,
可以得到5m=9;
加3
1
(2)若-3x=4.5,则x=-1.5,
这是根据等式的性质 ,
在等式两边同时 ;
(3)等式3x=2x+1两边同时 ,
得 ,
其根据是 .
等式的性质1
x=1
减2x
除以-3
2
9.利用等式的性质解下列方程并检验:
(1)y+3=2; (2)-y-2=3;
(3)9x=8x-6; (4)8m=4m+1.
y=-10
x=-6
y=-1
(检验略)
m=
★10.(北师7上P134)小虹遇到一个解方程的题:2x=5x,她选择的方法是两边同时除以x,竟然得到了2=5,她很苦恼,却找不到问题出在哪,你能帮她吗?
解:当x不等于0时,才能两边都除以x.
课堂小结:
1.等式的两个性质是解方程的重要依据,要求学生理解并掌握.
2.用方程解决实际问题时,先设未知数,再根据题意找等量关系,列方程求解,对所求得的解要进行检验
教材P83习题3.1,第2,4,11题
谢 谢
第三章 一元一次方程
3.1.2 等式的性质
教学目标:
【知识与技能】
(1)了解等式的概念和等式的两条性质.
(2)学会利用等式的两条性质解简单的一元一次方程.
【过程与方法】
利用天平进行实际操作,培养学生观察、分析、概括及逻辑思维能力,引导学生熟练地运用等式的性质解决问题.
【情感态度与价值观】
渗透“化归”的思想,增强主动探究的意识,发展合理的推理思维.
教学重难点:
1理解和运用等式的性质.
2利用等式的性质把简单的一元一次方程化成“x=a”的形式.
抽象能力 运算能力
模型观念 应用意识
1.(2022新课标)掌握等式的基本性质.
2.能利用等式的性质解一元一次方程.
知识点一:等式的性质
(1)等式的性质1:等式两边加(或减) (或式子),结果仍 ;
即:如果a=b,那么a±c= .
b±c
相等
同一个数
(2)等式的性质2:等式两边乘 ,或除以同一个不为0的数,结果仍相等;
即:如果a=b,那么ac= ;
如果a=b,c≠0,那么= .
在运用等式的性质2时,应注意:等式的两边除以的这个数不为0.
bc
同一个数
1.填空:
(1)在等式x+5=7的两边都 ,
得x=2,根据是 ;
(2)在等式x-3=8的两边都 ,
得x=11,根据是 ;
等式的性质1
加3
等式的性质1
减5
(3)在等式-=4的两边都 ,
得x=-12,根据是 ;
(4)如果-4x=-8,那么x= ,是等式两边都
得到的,根据是 .
等式的性质2
除以-4
2
等式的性质2
乘-3
知识点二:运用等式的性质解方程
利用等式的性质解方程的目的是将方程一步一步地变形为
x=a(常数)的形式,步骤如下:
(1)方程两边加(或减)同一个数(或式子),使一元一次方程左边是含 的项,右边是 项;
常数
未知数
(2)方程两边乘同一个数或除以同一个不为0的数,使未知数的 化为1,从而得出方程的解.
检验某数是不是某方程的解,方法是把这个数分别代入方程的左边和右边,注意“分别”看方程左、右两边的值是否
,若 ,则是方程的解;若 ,则不是.
不相等
相等
相等
系数
2.(北师7上P133)尝试运用等式的性质解一元一次方程.
(1)x+2=5.
解:方程的两边同时 ,
得 .
于是,x= .
反思:这道题应用了等式的性质 来解决.
1
3
x+2-2=5-2
减2
(2)-3x=15.
解:方程的两边同时 ,
得 .
于是,x= .
反思:这道题应用了等式的性质 来解决.
2
-5
-3x÷(-3)=15÷(-3)
除以-3
(3)3-x=9(并检验).
解:方程的两边同时减去 ,
得 .化简,得____________.
方程的两边同时乘 ,得x= .
检验:将 分别代入方程左右两边,左边= ,右边= ,因为 ,
所以 .
反思:这道题应用了等式的性质 与等式的性质 来解决.
-x=6
3-x-3=9-3
2
1
x=-18是原方程的解
左边=右边
9
9
x=-18
-18
-3
3
小结:利用等式的性质对等式进行变形时,等式两边要同时进行相同的运算,注意“0”不能作为除数和分母.
3.【例1】若a=b,下列各式不正确的是( )
A.a+9=b+9 B.-2a=-2b
C.a-7=b+7 D.
C
4.【例2】填空:
(1)已知等式x+3=-2,根据等式的性质1,两边
,得到x= ;
(2)已知等式x=6,根据等式的性质2,两边 ,得到x= ;
同时除以
9
-5
同时减去3
小结:等式的变形先要联想到等式的性质,再仔细观察、分析前后两个等式的结构有何变化,从而确定是应用哪条性质.
(3)已知等式6y=2y-4,根据等式的性质1,两边
,得到4y= ,再根据等式的性质2,两边 ,得到 .
y=-1
同时除以4
-4
同时减去2y
5.【例3】(人教7上P82、北师7上P133)利用等式的性质解下列方程并检验:
(1)x+7=26; (2)-5x=20;
(3)-x-5=4.
x=-4
x=-27
x=19
(检验略)
小结:利用等式的性质解方程,实质就是将方程一步步转化为x=a(a为常数)的形式.把x的值代入检验时,等号左右两边的值相等,否则x的值不是方程的解.
小结:先设未知数,再找出相等关系列方程.
6.【例4】列一元一次方程,不求解:
某超市销售有甲、乙两种商品,甲商品每件进价10元,乙商品每件进价30元.若该超市同时一次购进甲、乙两种商品共80件,恰好用去1 600元,能购进甲、乙两种商品各多少件?
.
解:设购进甲商品x件,得10x+30(80-x)=1 600.
7.下列等式的变形中,不正确的是( )
A.若x=y,则x+5=y+5
B.若(a≠0),则x=y
C.若-3x=-3y,则x=y
D.若mx=my,则x=y
D
8.填空:
(1)已知等式5m-3=6,
根据等式的性质 ,
两边同时 ,
可以得到5m=9;
加3
1
(2)若-3x=4.5,则x=-1.5,
这是根据等式的性质 ,
在等式两边同时 ;
(3)等式3x=2x+1两边同时 ,
得 ,
其根据是 .
等式的性质1
x=1
减2x
除以-3
2
9.利用等式的性质解下列方程并检验:
(1)y+3=2; (2)-y-2=3;
(3)9x=8x-6; (4)8m=4m+1.
y=-10
x=-6
y=-1
(检验略)
m=
★10.(北师7上P134)小虹遇到一个解方程的题:2x=5x,她选择的方法是两边同时除以x,竟然得到了2=5,她很苦恼,却找不到问题出在哪,你能帮她吗?
解:当x不等于0时,才能两边都除以x.
课堂小结:
1.等式的两个性质是解方程的重要依据,要求学生理解并掌握.
2.用方程解决实际问题时,先设未知数,再根据题意找等量关系,列方程求解,对所求得的解要进行检验
教材P83习题3.1,第2,4,11题
谢 谢
