《1.3三角函数的计算》优秀教案 数学北师大版 九年级下册
文档属性
| 名称 | 《1.3三角函数的计算》优秀教案 数学北师大版 九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 424.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 21:01:22 | ||
图片预览


文档简介
第一章 直角三角形的边角关系
1.3 三角函数的计算
一、教学目标
1.经历用计算器由已知锐角求它的三角函数值及由三角函数值求相应的锐角的过程,进一步体会三角函数的意义.
2.能够运用计算器进行有关三角函数值的计算.
3.能够运用计算器辅助解决三角函数值计算的实际问题.
二、教学重点及难点
重点:熟悉计算器的使用,能熟练地掌握按键顺序.
难点:非整度数的角的三角函数值的求法.
三、教学用具
多媒体课件、直尺或三角板。
四、相关资源
《缆车运行》动画.
五、教学过程
【情境引入】
【情景演示】登山缆车,此动画展现出三角函数在登山缆车中的应用。
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200 m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
在Rt△ ABC中,∠ACB=90°,BC=ABsin16°.你知道sin16°是多少吗?我们可以借助科学计算器求锐角的三角函数值.那么怎样用科学计算器求三角函数值呢?这节课我们就来研究这个问题.
师生活动:教师出示问题,学生观察、思考、讨论.
设计意图:由实际问题引出本节课要研究的内容,激发学生的学习欲望.
【探究新知】
用科学计算器求三角函数值,要用到和键.例如,求sin16°,cos72°38′25″和tan85°的按键顺序如下所示.
sin16°,按键顺序:,显示结果:sin16°=0.275 637 355 8.
cos72°38′25″,按键顺序:,
显示结果:cos72°38′25″=0.298 369 906 7.
tan85°,按键顺序:,tan85°=11.430 052 3.
对于本节课开始提出的问题,利用科学计算器可以求得BC=200 sin16°≈55.12(m).
议一议 在本节课开始提出的问题中,当缆车继续由点B到达点D时,他又走过了200m,缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么?
师生活动:教师出示问题,学生思考、讨论.
答:这是一个开放性问题,答案不唯一,例如,可以计算出缆车由点B到点D时,上升的高度和水平移动的距离等.
设计意图:通过该问题的探究,培养学生提出问题、分析问题、解决问题的能力.
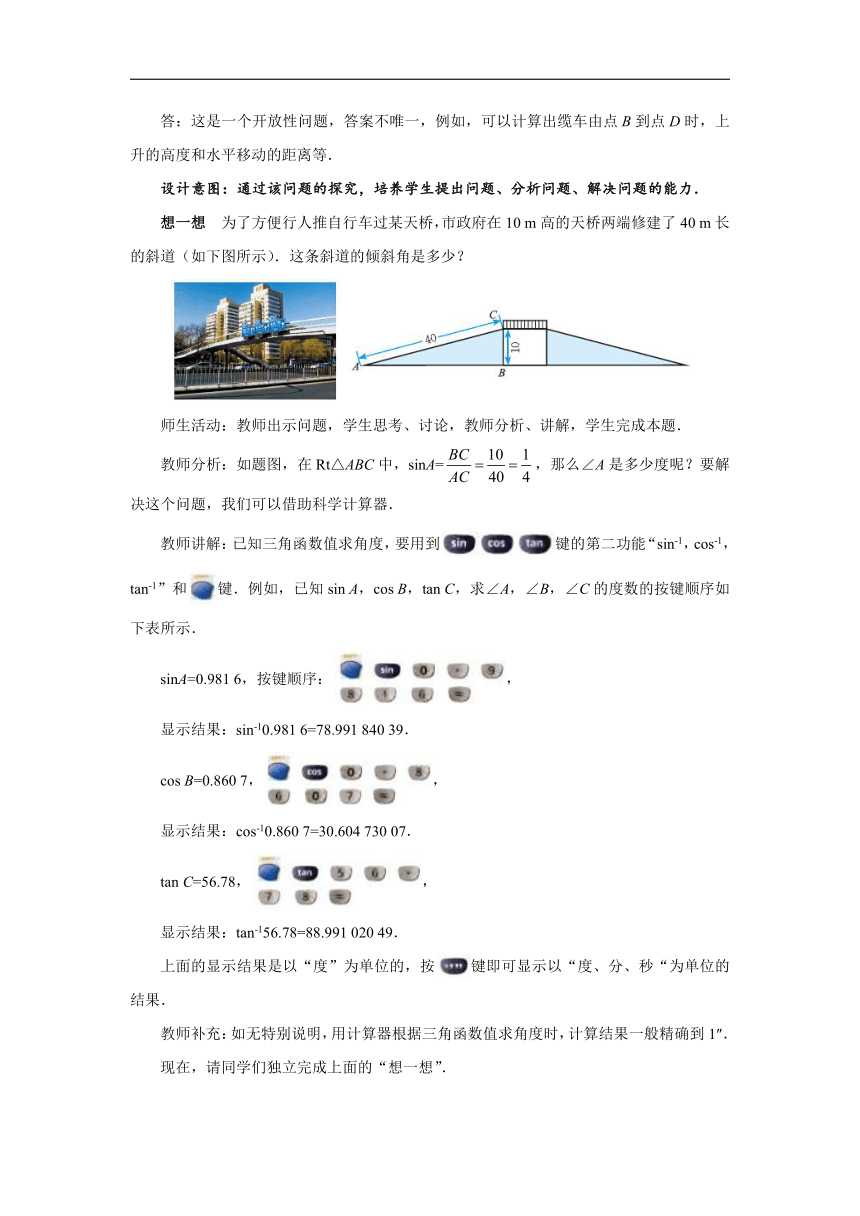
想一想 为了方便行人推自行车过某天桥,市政府在10 m高的天桥两端修建了40 m长的斜道(如下图所示).这条斜道的倾斜角是多少?
师生活动:教师出示问题,学生思考、讨论,教师分析、讲解,学生完成本题.
教师分析:如题图,在Rt△ABC中,sinA=,那么∠A是多少度呢?要解决这个问题,我们可以借助科学计算器.
教师讲解:已知三角函数值求角度,要用到键的第二功能“sin-1,cos-1,tan-1”和键.例如,已知sin A,cos B,tan C,求∠A,∠B,∠C的度数的按键顺序如下表所示.
sinA=0.981 6,按键顺序:,
显示结果:sin-10.981 6=78.991 840 39.
cos B=0.860 7,,
显示结果:cos-10.860 7=30.604 730 07.
tan C=56.78,,
显示结果:tan-156.78=88.991 020 49.
上面的显示结果是以“度”为单位的,按键即可显示以“度、分、秒“为单位的结果.
教师补充:如无特别说明,用计算器根据三角函数值求角度时,计算结果一般精确到1″.
现在,请同学们独立完成上面的“想一想”.
解:∵在Rt△ABC中,sinA=,∴∠A≈14°28′39″.
答:∠A的度数约为14°28′39″.
设计意图:由实际问题引出计算角度的问题,使学生体会数学和实际生活的密切联系,激发学生的学习热情.
【典例精析】
例1 用计算器求下列三角函数的值(结果精确到0.0001).
(1)sin 46°25′40″;(2)cos56°40′;(3)tan 46°35′20″.
师生活动:教师出示例题,学生完成解答.
解:(1)sin 46°25′40″≈0.7245;(2)cos56°40′≈0.5495;(3)tan 46°35′20″≈1.0571.
例2 已知下列锐角三角函数值,求出其对应锐角的度数.
(1)sin A=0.2046;(2)cosA=0.7958;(3)tan A=3.280.
师生活动:教师出示例题,学生完成解答.
解:(1)∠A≈11.81°或11°48′22″;(2)∠A≈37.27°或37°16′9″;(3)∠A≈73.04°或73°2′41″.
设计意图:让学生巩固所学知识,加深对所学知识的理解.
【课堂练习】
1.用计算器求下列各式的值:
(1)sin56°;(2)cos20.5°;(3)tan44°59′59″;(4)sin15°+cos61°+tan76°.
2.已知sinθ=0.82904,求锐角θ的度数.
师生活动:教师先找几名学生板演,然后讲解出现的问题.
3.一个人由山底爬到山顶,需先爬坡角为40°的山坡100 m,再爬坡角为30°的山坡100 m,求山高(结果精确到0.1 m).
4.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成锐角的度数.
参考答案
1.(1)sin56°≈0.829 0;(2)cos20.5°≈0.936 7;(3)tan44°59′59″≈1.000 0;
(4)sin15°+cos61°+tan76°≈4.754 4.
2.∵sinθ=0.829 04,∴θ≈56°1″.
3.山高约242.8 m.
4.梯子与地面所成锐角的度数约为51°19′4″.
设计意图:通过学生自主练习,可以查看学生答题的情况,统计差错及目标达成率,也可以让学生真正地动手、动脑,从而达到很好地掌握知识的目的.
六、课堂小结
这节课我们主要学习了:
计算器的使用方法;
2.整度数角的三角函数值的求法;
3.非整度数角的三角函数值的求法;
4.用计算器由锐角三角函数值求相应锐角大小的方法.
师生活动:教师引导学生归纳、总结本节课所学内容.
设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
七、板书设计
1.3 三角函数的计算
1.计算器的使用方法;
2.三角函数值的求法;
3.由锐角三角函数值求相应锐角
(六)布置作业
1.用计算器求下列各式的值:
(1)tan32°;(2)cos24.53°;(3)sin62°11′;(4)tan39°39′39″.
4.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成锐角的度数.
参考答案
1.(1)tan32°≈0.624 9;(2)cos24.53°≈0.909 7;(3)sin62°11′≈0.884 4;
(4)tan39°39′39″≈0.829 1.
4.梯子与地面所成锐角的度数约为51°19′4″.
四、课堂检测设计
1.用计算器求下列各式的值:
(1)sin256°+cos225°;(2)sin62.6°-2sin37°·cos20°.
2.根据下列条件求锐角θ的度数:
(1)tanθ=2.988 8;(2)sinθ=0.395 7;(3)cosθ=0.785 0;(4)tanθ=0.897 2.
3.一个人由山底爬到山顶,需先爬坡角为40°的山坡300 m,再爬坡角为30°的山坡100 m.求山高(结果精确到0.1 m).
参考答案
1.(1)1.508 7;(2)-0.243 2.
2.(1)θ≈71°30′2″;(2)θ≈23°18′35″;(3)θ≈38°16′46″;(4)θ≈41°53′54″.
3.山高约为242.8 m.
1.3 三角函数的计算
一、教学目标
1.经历用计算器由已知锐角求它的三角函数值及由三角函数值求相应的锐角的过程,进一步体会三角函数的意义.
2.能够运用计算器进行有关三角函数值的计算.
3.能够运用计算器辅助解决三角函数值计算的实际问题.
二、教学重点及难点
重点:熟悉计算器的使用,能熟练地掌握按键顺序.
难点:非整度数的角的三角函数值的求法.
三、教学用具
多媒体课件、直尺或三角板。
四、相关资源
《缆车运行》动画.
五、教学过程
【情境引入】
【情景演示】登山缆车,此动画展现出三角函数在登山缆车中的应用。
如图,当登山缆车的吊箱经过点A到达点B时,它走过了200 m.已知缆车行驶的路线与水平面的夹角为∠α=16°,那么缆车垂直上升的距离是多少?(结果精确到0.01 m)
在Rt△ ABC中,∠ACB=90°,BC=ABsin16°.你知道sin16°是多少吗?我们可以借助科学计算器求锐角的三角函数值.那么怎样用科学计算器求三角函数值呢?这节课我们就来研究这个问题.
师生活动:教师出示问题,学生观察、思考、讨论.
设计意图:由实际问题引出本节课要研究的内容,激发学生的学习欲望.
【探究新知】
用科学计算器求三角函数值,要用到和键.例如,求sin16°,cos72°38′25″和tan85°的按键顺序如下所示.
sin16°,按键顺序:,显示结果:sin16°=0.275 637 355 8.
cos72°38′25″,按键顺序:,
显示结果:cos72°38′25″=0.298 369 906 7.
tan85°,按键顺序:,tan85°=11.430 052 3.
对于本节课开始提出的问题,利用科学计算器可以求得BC=200 sin16°≈55.12(m).
议一议 在本节课开始提出的问题中,当缆车继续由点B到达点D时,他又走过了200m,缆车由点B到点D的行驶路线与水平面的夹角为∠β=42°,由此你还能计算什么?
师生活动:教师出示问题,学生思考、讨论.
答:这是一个开放性问题,答案不唯一,例如,可以计算出缆车由点B到点D时,上升的高度和水平移动的距离等.
设计意图:通过该问题的探究,培养学生提出问题、分析问题、解决问题的能力.
想一想 为了方便行人推自行车过某天桥,市政府在10 m高的天桥两端修建了40 m长的斜道(如下图所示).这条斜道的倾斜角是多少?
师生活动:教师出示问题,学生思考、讨论,教师分析、讲解,学生完成本题.
教师分析:如题图,在Rt△ABC中,sinA=,那么∠A是多少度呢?要解决这个问题,我们可以借助科学计算器.
教师讲解:已知三角函数值求角度,要用到键的第二功能“sin-1,cos-1,tan-1”和键.例如,已知sin A,cos B,tan C,求∠A,∠B,∠C的度数的按键顺序如下表所示.
sinA=0.981 6,按键顺序:,
显示结果:sin-10.981 6=78.991 840 39.
cos B=0.860 7,,
显示结果:cos-10.860 7=30.604 730 07.
tan C=56.78,,
显示结果:tan-156.78=88.991 020 49.
上面的显示结果是以“度”为单位的,按键即可显示以“度、分、秒“为单位的结果.
教师补充:如无特别说明,用计算器根据三角函数值求角度时,计算结果一般精确到1″.
现在,请同学们独立完成上面的“想一想”.
解:∵在Rt△ABC中,sinA=,∴∠A≈14°28′39″.
答:∠A的度数约为14°28′39″.
设计意图:由实际问题引出计算角度的问题,使学生体会数学和实际生活的密切联系,激发学生的学习热情.
【典例精析】
例1 用计算器求下列三角函数的值(结果精确到0.0001).
(1)sin 46°25′40″;(2)cos56°40′;(3)tan 46°35′20″.
师生活动:教师出示例题,学生完成解答.
解:(1)sin 46°25′40″≈0.7245;(2)cos56°40′≈0.5495;(3)tan 46°35′20″≈1.0571.
例2 已知下列锐角三角函数值,求出其对应锐角的度数.
(1)sin A=0.2046;(2)cosA=0.7958;(3)tan A=3.280.
师生活动:教师出示例题,学生完成解答.
解:(1)∠A≈11.81°或11°48′22″;(2)∠A≈37.27°或37°16′9″;(3)∠A≈73.04°或73°2′41″.
设计意图:让学生巩固所学知识,加深对所学知识的理解.
【课堂练习】
1.用计算器求下列各式的值:
(1)sin56°;(2)cos20.5°;(3)tan44°59′59″;(4)sin15°+cos61°+tan76°.
2.已知sinθ=0.82904,求锐角θ的度数.
师生活动:教师先找几名学生板演,然后讲解出现的问题.
3.一个人由山底爬到山顶,需先爬坡角为40°的山坡100 m,再爬坡角为30°的山坡100 m,求山高(结果精确到0.1 m).
4.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成锐角的度数.
参考答案
1.(1)sin56°≈0.829 0;(2)cos20.5°≈0.936 7;(3)tan44°59′59″≈1.000 0;
(4)sin15°+cos61°+tan76°≈4.754 4.
2.∵sinθ=0.829 04,∴θ≈56°1″.
3.山高约242.8 m.
4.梯子与地面所成锐角的度数约为51°19′4″.
设计意图:通过学生自主练习,可以查看学生答题的情况,统计差错及目标达成率,也可以让学生真正地动手、动脑,从而达到很好地掌握知识的目的.
六、课堂小结
这节课我们主要学习了:
计算器的使用方法;
2.整度数角的三角函数值的求法;
3.非整度数角的三角函数值的求法;
4.用计算器由锐角三角函数值求相应锐角大小的方法.
师生活动:教师引导学生归纳、总结本节课所学内容.
设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
七、板书设计
1.3 三角函数的计算
1.计算器的使用方法;
2.三角函数值的求法;
3.由锐角三角函数值求相应锐角
(六)布置作业
1.用计算器求下列各式的值:
(1)tan32°;(2)cos24.53°;(3)sin62°11′;(4)tan39°39′39″.
4.一梯子斜靠在一面墙上.已知梯长4 m,梯子位于地面上的一端离墙壁2.5 m,求梯子与地面所成锐角的度数.
参考答案
1.(1)tan32°≈0.624 9;(2)cos24.53°≈0.909 7;(3)sin62°11′≈0.884 4;
(4)tan39°39′39″≈0.829 1.
4.梯子与地面所成锐角的度数约为51°19′4″.
四、课堂检测设计
1.用计算器求下列各式的值:
(1)sin256°+cos225°;(2)sin62.6°-2sin37°·cos20°.
2.根据下列条件求锐角θ的度数:
(1)tanθ=2.988 8;(2)sinθ=0.395 7;(3)cosθ=0.785 0;(4)tanθ=0.897 2.
3.一个人由山底爬到山顶,需先爬坡角为40°的山坡300 m,再爬坡角为30°的山坡100 m.求山高(结果精确到0.1 m).
参考答案
1.(1)1.508 7;(2)-0.243 2.
2.(1)θ≈71°30′2″;(2)θ≈23°18′35″;(3)θ≈38°16′46″;(4)θ≈41°53′54″.
3.山高约为242.8 m.
