苏教版选择性必修第一册3.2.2双曲线的几何性质同步教学 课件(共48张PPT)
文档属性
| 名称 | 苏教版选择性必修第一册3.2.2双曲线的几何性质同步教学 课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 14:05:27 | ||
图片预览











文档简介
(共48张PPT)
第3章 圆锥曲线与方程
3.2.2 双曲线的几何性质
课标要求
1.了解双曲线的简单几何性质.2.会求双曲线的渐近线、离心率、顶点、焦点坐标等.3.知道椭圆与双曲线几何性质的区别.
素养要求
1.通过双曲线几何性质的学习,提升直观想象素养.2.借助双曲线几何性质的应用,提升数学运算素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
一、双曲线的简单几何性质
1.思考 椭圆中长轴长大于短轴长,双曲线中,实轴长一定大于虚轴长吗?
提示 实轴长不一定大于虚轴长.
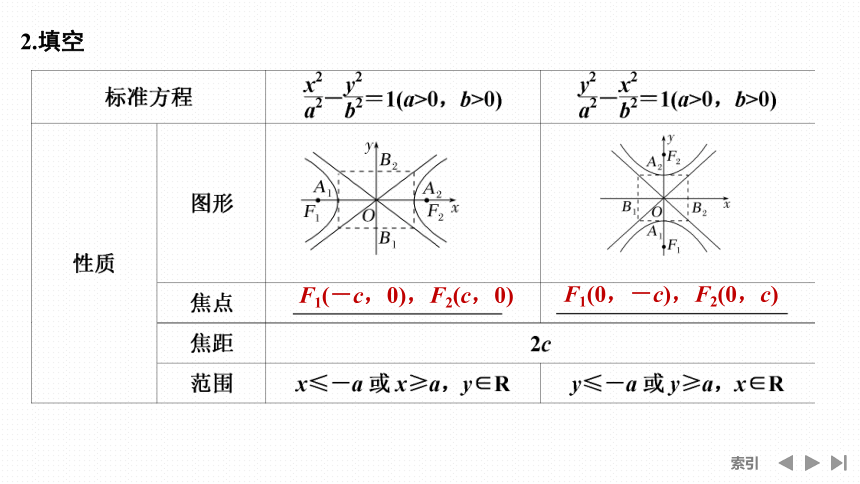
2.填空
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
x轴,y轴
原点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
2a
2b
a
b
(1,+∞)
B
二、等轴双曲线
1.思考 双曲线x2-y2=1的实轴长、虚轴长、离心率、渐近线方程是什么?
2.填空 (1)实轴和虚轴______的双曲线叫作等轴双曲线.
等长
±x
垂直
ACD
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
题型一 双曲线的几何性质
迁移 求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准方程是解决本题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
思维升华
训练1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
例2 分别求适合下列条件的双曲线的标准方程:
题型二 根据几何性质求双曲线的标准方程
思维升华
训练2 根据下列条件分别求双曲线的标准方程:
D
题型三 求双曲线的离心率
思维升华
解析 不妨设PF1>PF2,则PF1-PF2=2a,又PF1+PF2=6a,
所以PF1=4a,PF2=2a,又F1F2=2c,则在△PF1F2中,∠PF1F2=30°,
课堂小结
1.牢记双曲线的9个性质
2.掌握研究双曲线几何性质的2种方法
(1)求双曲线的方法.
(2)求离心率的方法.
3.注意2个易错点
(1)忽略焦点在哪条坐标轴上的讨论而致错.
(2)混淆双曲线与椭圆的离心率的范围而致误.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
1.双曲线3x2-y2=3的渐近线方程是( )
C
2.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线的方程为( )
A
D
AC
D
∴3b=4a,
∴9(c2-a2)=16a2,
∴9c2=25a2,∴3c=5a,
4
(4,+∞)
②当双曲线的焦点在y轴上时,
D
D
解 依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,得
(1-k2)x2-4kx-6=0.
∵直线l与双曲线C交于不同的两点E,F,
±1
本课结束
第3章 圆锥曲线与方程
3.2.2 双曲线的几何性质
课标要求
1.了解双曲线的简单几何性质.2.会求双曲线的渐近线、离心率、顶点、焦点坐标等.3.知道椭圆与双曲线几何性质的区别.
素养要求
1.通过双曲线几何性质的学习,提升直观想象素养.2.借助双曲线几何性质的应用,提升数学运算素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
一、双曲线的简单几何性质
1.思考 椭圆中长轴长大于短轴长,双曲线中,实轴长一定大于虚轴长吗?
提示 实轴长不一定大于虚轴长.
2.填空
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
x轴,y轴
原点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
2a
2b
a
b
(1,+∞)
B
二、等轴双曲线
1.思考 双曲线x2-y2=1的实轴长、虚轴长、离心率、渐近线方程是什么?
2.填空 (1)实轴和虚轴______的双曲线叫作等轴双曲线.
等长
±x
垂直
ACD
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
题型一 双曲线的几何性质
迁移 求双曲线nx2-my2=mn(m>0,n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.
由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准方程是解决本题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
思维升华
训练1 求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
例2 分别求适合下列条件的双曲线的标准方程:
题型二 根据几何性质求双曲线的标准方程
思维升华
训练2 根据下列条件分别求双曲线的标准方程:
D
题型三 求双曲线的离心率
思维升华
解析 不妨设PF1>PF2,则PF1-PF2=2a,又PF1+PF2=6a,
所以PF1=4a,PF2=2a,又F1F2=2c,则在△PF1F2中,∠PF1F2=30°,
课堂小结
1.牢记双曲线的9个性质
2.掌握研究双曲线几何性质的2种方法
(1)求双曲线的方法.
(2)求离心率的方法.
3.注意2个易错点
(1)忽略焦点在哪条坐标轴上的讨论而致错.
(2)混淆双曲线与椭圆的离心率的范围而致误.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
1.双曲线3x2-y2=3的渐近线方程是( )
C
2.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线的方程为( )
A
D
AC
D
∴3b=4a,
∴9(c2-a2)=16a2,
∴9c2=25a2,∴3c=5a,
4
(4,+∞)
②当双曲线的焦点在y轴上时,
D
D
解 依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,得
(1-k2)x2-4kx-6=0.
∵直线l与双曲线C交于不同的两点E,F,
±1
本课结束
