北师大版九年级下册第一章 直角三角形的边角关系:《30°,45°,60°角的三角函数值》同步习题(含答案)
文档属性
| 名称 | 北师大版九年级下册第一章 直角三角形的边角关系:《30°,45°,60°角的三角函数值》同步习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 226.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 09:15:10 | ||
图片预览

文档简介
《30°、45°、60°角的三角函数值》同步练习
1.在中,,,则的值是( )
A. B. C. D.
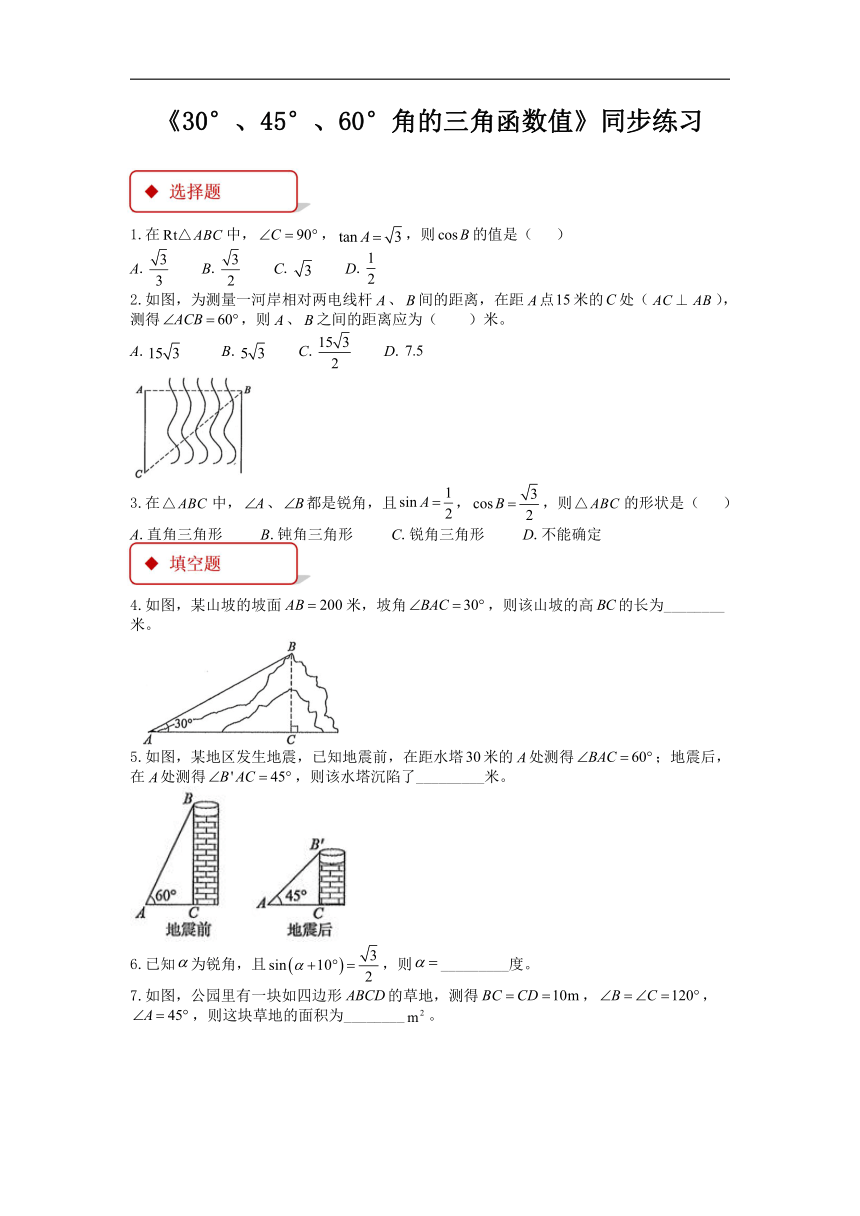
2.如图,为测量一河岸相对两电线杆、间的距离,在距点米的处(),测得,则、之间的距离应为( )米。
A. B. C. D.
3.在中,、都是锐角,且,,则的形状是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
4.如图,某山坡的坡面米,坡角,则该山坡的高的长为________米。
5.如图,某地区发生地震,已知地震前,在距水塔米的处测得;地震后,在处测得,则该水塔沉陷了_________米。
6.已知为锐角,且,则_________度。
7.如图,公园里有一块如四边形的草地,测得,,,则这块草地的面积为________。
8.计算:
(1);
(2);
(3)。
9.如图,已知,点在边上,,点、在边上,,,求。
10.如图(1)为平地上一幢建筑物与铁塔图,图(2)为其示意图,小苏用一个两锐角分别为和的三角尺测量铁塔的高度.已知,求铁塔的高度。
答案与解析
1.B
2.A
3.B
4.
5.
6.,分析:根据特殊角的三角函数值即可求得α角的度数。
7.,分析:连接BD,找到特殊角的三角形,再利用三角形面积
公式即可求解。
8.(1),(2),(3)
9.,分析:过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函
数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据
MN求出MD的长,由OD-MD即可求出OM的长。
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°=OD/OP=1/2,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=1/2MN=1,
∴OM=OD-MD=6-1=5。
10.
1.在中,,,则的值是( )
A. B. C. D.
2.如图,为测量一河岸相对两电线杆、间的距离,在距点米的处(),测得,则、之间的距离应为( )米。
A. B. C. D.
3.在中,、都是锐角,且,,则的形状是( )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定
4.如图,某山坡的坡面米,坡角,则该山坡的高的长为________米。
5.如图,某地区发生地震,已知地震前,在距水塔米的处测得;地震后,在处测得,则该水塔沉陷了_________米。
6.已知为锐角,且,则_________度。
7.如图,公园里有一块如四边形的草地,测得,,,则这块草地的面积为________。
8.计算:
(1);
(2);
(3)。
9.如图,已知,点在边上,,点、在边上,,,求。
10.如图(1)为平地上一幢建筑物与铁塔图,图(2)为其示意图,小苏用一个两锐角分别为和的三角尺测量铁塔的高度.已知,求铁塔的高度。
答案与解析
1.B
2.A
3.B
4.
5.
6.,分析:根据特殊角的三角函数值即可求得α角的度数。
7.,分析:连接BD,找到特殊角的三角形,再利用三角形面积
公式即可求解。
8.(1),(2),(3)
9.,分析:过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函
数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据
MN求出MD的长,由OD-MD即可求出OM的长。
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°=OD/OP=1/2,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=1/2MN=1,
∴OM=OD-MD=6-1=5。
10.
