苏教版选择性必修第一册5.3.2极大值与极小值 课件(共61张PPT)
文档属性
| 名称 | 苏教版选择性必修第一册5.3.2极大值与极小值 课件(共61张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 17:19:12 | ||
图片预览











文档简介
(共61张PPT)
第5章 导数及其应用
5.3.2 极大值与极小值
课标要求
1.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件.2.能利用导数求某些函数的极大值、极小值.
素养要求
通过理解函数的极值及其应用导数求极值的过程,发展学生的直观想象与数学运算素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
一、函数极大(小)值的概念
1.思考 (1)如图是某处群山的截面图,你能指出山峰、山谷吗?
提示 在x1,x3,x5处是山峰,在x2,x4处是山谷.
(2)你能描述一下在各个山峰、山谷附近的特点吗?
提示 以山峰x=x1处为例来研究,在x=x1处,它附近的函数值都比它小,且在x=x1处的左侧函数是单调递增的,且有f′(x)>0,在x=x1处的右侧函数是单调递减的,且有f′(x)<0,函数图象是连续不断的,f′(x)的变化也是连续不断的,并且有f′(x1)=0.
2.填空 一般地,若存在δ>0,当x∈(x1-δ,x1+δ)时,都有_______________,则称f(x1)为函数f(x)的一个极大值;类似地,若存在δ>0,当x∈(x2-δ,x2+δ)时,都有_________________,则称f(x2)为函数f(x)的一个极小值.
函数的极大值、极小值统称为函数的______.
f(x) ≤f(x1)
f(x)≥f(x2)
极值
温馨提醒 (1)极值是一个局部性概念.由极值的定义知,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个定义域内最大或最小,即反映的是函数在某一点附近的大小情况.
(2)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.
3.做一做 已知函数f(x)的导函数f′(x)的图象如图所示,则函数f(x)有( )
C
A.两个极大值,一个极小值
B.两个极大值,无极小值
C.一个极大值,一个极小值
D.一个极大值,两个极小值
解析 由图可知导函数f′(x)有三个零点,依次设为x1<0,x2=0,x3>0,当x0,所以函数f(x)在x=x1处取得极小值;当x10,当x20,所以函数f(x)在x=x2处无极值;又当x>x3时,f′(x)<0,所以函数f(x)在x=x3处取得极大值,故选C.
二、函数的极值与导数的关系
1.思考 导数为0的点一定是极值点吗?
提示 不一定.反例:f(x)=x3,f′(x)=3x2,f′(0)=0,但x=0不是f(x)=x3的极值点.
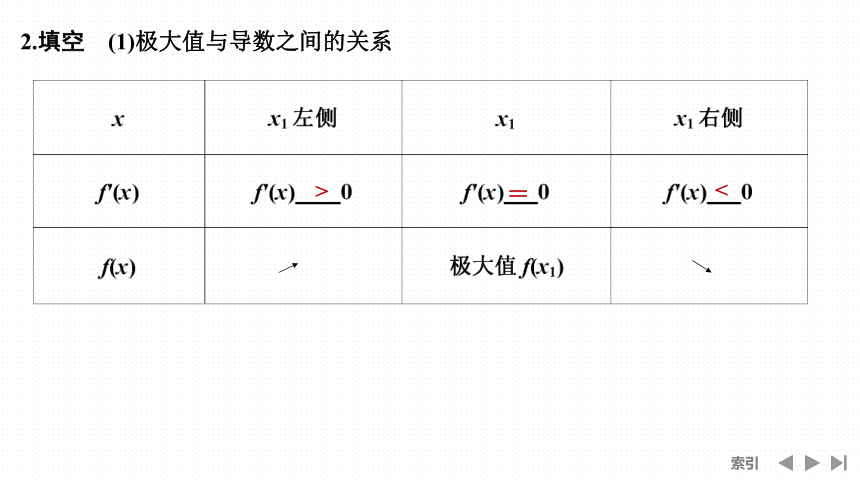
2.填空 (1)极大值与导数之间的关系
>
=
<
(2)极小值与导数之间的关系
<
=
>
温馨提醒 函数的极值是函数的局部性质,可导函数f(x)在点x=x0处取得极值的充要条件是f′(x0)=0且在x=x0两侧f′(x)符号相反.
-3
解析 f′(x)=x2-2x-3,
令f′(x)>0,得x<-1或x>3,
令f′(x)<0得-1故f(x)在(-∞,-1),(3,+∞)上单调递增,在(-1,3)上单调递减,
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
角度1 不含参数的函数求极值
例1 求下列函数的极值:
题型一 求函数的极值
(1)f(x)=(x3-1)2+1;
解 ∵f(x)=(x3-1)2+1=x6-2x3+2,
∴f(x)的定义域为R,
f′(x)=6x5-6x2=6x2(x3-1).
令f′(x)=0,得x=0或x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) ? 3 ?
求可导函数f(x)的极值的步骤
(1)确定函数的定义域,求导数f′(x);
(2)求方程f′(x)=0的根;
(3)用函数的导数为0的点,顺次将函数的定义域分成若干个小开区间,并列成表格.检测f′(x)在方程根左右两侧的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值.
思维升华
训练1 求函数f(x)=x2e-x的极值.
解 函数f(x)的定义域为R,
f′(x)=2xe-x+x2·e-x·(-x)′=2xe-x-x2e-x=x(2-x)e-x.
令f′(x)=0,得x(2-x)e-x=0,解得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
因此当x=0时,f(x)取得极小值,且极小值为f(0)=0;
角度2 含参数的函数求极值
解 f′(x)=[x2+(a+2)x-2a2+4a]ex.
令f′(x)=0,解得x=-2a或x=a-2,
当x变化时,f′(x),f(x)的变化情况如下表:
要掌握函数极值的求法,需注意:
导数值为0的点将整个定义域分为若干个区间,可将x,f′(x),f(x)在每个区间内的变化情况列在一个表格中,通过表格可以判断在哪个点处取得极值,是极大值还是极小值.如下两表:
思维升华
由表格可清晰地看出极值的分布情况,对于初学者是首选;后期对求导比较熟练时也可以省去列表格.
训练2 已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
②当a>0时,由f′(x)=0,解得x=a;
∵x∈(0,a)时,f′(x)<0,x∈(a,+∞)时,f′(x)>0,
∴f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
例3 已知函数f(x)=ax3+bx2+cx(a≠0)在x=±1处取得极值,且f(1)=-1.
(1)求常数a,b,c的值;
题型二 利用函数极值确定参数的值
解 f′(x)=3ax2+2bx+c.
∵x=±1是函数f(x)的极值点,
∴x=±1是方程f′(x)=3ax2+2bx+c=0的两根,
又f(1)=-1,
∴a+b+c=-1. ③
(2)判断x=±1是函数的极大值点还是极小值点,试说明理由,并求出极值.
当x<-1或x>1时,f′(x)>0,
当-1∴函数f(x)在(-∞,-1)和(1,+∞)上是增函数,在(-1,1)上是减函数,
∴当x=-1时,函数取得极大值f(-1)=1,
当x=1时,函数取得极小值f(1)=-1.
已知函数极值,确定函数解析式中的参数时,注意两点
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解;
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
思维升华
训练3 已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值.
当a=1,b=3时,
f′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,f′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈(-3,-1)时,f′(x)<0,f(x)为减函数;
当x∈(-∞,-3)和(-1,+∞)时,f′(x)>0,f(x)为增函数,
所以f(x)在x=-1时取得极小值,因此a=2,b=9.
题型三 极值的综合应用
例4 已知函数f(x)=x3-3x+a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围.
解 令f′(x)=3x2-3=3(x+1)(x-1)=0,
解得x1=-1,x2=1.
当x<-1时,f′(x)>0;
当-1当x>1时,f′(x)>0.
所以当x=-1时,
f(x)有极大值f(-1)=2+a;
当x=1时,f(x)有极小值f(1)=-2+a.
因为方程f(x)=0有三个不同实根,
所以y=f(x)的图象与x轴有三个交点,如图.
迁移1 (改变条件)本例中,若方程f(x)=0恰有两个根,则实数a的值如何求解?
解 由例题,知函数的极大值f(-1)=2+a,极小值f(1)=-2+a,
若f(x)=0恰有两个根,则有2+a=0,或-2+a=0,
所以a=-2或a=2.
迁移2 本例中,若方程f(x)=0有且只有一个实根,求实数a的取值范围.
解 由例题可知,要使方程f(x)=0有且只有一个实根,
只需2+a<0或-2+a>0,即a<-2或a>2.故a的取值范围为
(-∞,-2)∪(2,+∞).
利用导数可以判断函数的单调性,研究函数的极值情况,并能在此基础上画出函数的大致图象,从直观上判断函数图象与x轴的交点或两个函数图象的交点个数,从而为研究方程根的个数问题提供了方便.
思维升华
(2)若函数y=f(x)-m仅有一个零点,求实数m的取值范围.
解 由(1),知当x>0时,f(x)=(x2-2x)ex,f′(x)=(x2-2)ex.
课堂小结
1.牢记2个知识点
(1)极值的概念.
(2)极值与导数的关系.
2.掌握2种方法
(1)求极值的方法.
(2)已知极值求函数解析式的方法.
3.注意1个易错点
对极值的充要条件把握不准致错.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
1.下列函数中存在极值的是( )
B
解析 对于y=x-ex,y′=1-ex,x∈R,
令y′=0,得x=0.
在区间(-∞,0)上,y′>0;
在区间(0,+∞)上,y′<0.
故x=0为函数y=x-ex的极大值点.
2.函数f(x)=(x-1)ex的极小值点为( )
A.(0,-1) B.(0,0)
C.-1 D.0
D
解析 由题意得f′(x)=ex+(x-1)ex=xex,x∈R,故f(x)在(-∞,0)上是减函数,在(0,+∞)上是增函数,
故当x=0时,f(x)的极小值为f(0)=-1,故极小值点为0.
3.(多选)定义在R上的可导函数y=f(x)的导函数的图象如图所示,以下结论正确的是( )
ACD
A.-3是f(x)的一个极小值点
B.-2和-1都是f(x)的极大值点
C.f(x)的单调递增区间是(-3,+∞)
D.f(x)的单调递减区间是(-∞,-3)
解析 当x<-3时,f′(x)<0,x∈(-3,+∞)时f′(x)≥0,∴-3是极小值点,无极大值点,增区间是(-3,+∞),减区间是(-∞,-3).故选ACD.
4.函数f(x)=x3+ax2+bx+a2+a在x=1处有极值为7,则a等于( )
A.-3或3 B.3或-9 C.3 D.-3
C
解析 f′(x)=3x2+2ax+b,
当a=3,b=-9时,f′(x)=3x2+6x-9=3(x-1)(x+3),当-31时,f′(x)>0,x=1是极小值点;
当a=-3,b=3时,f′(x)=3x2-6x+3=3(x-1)2≥0,x=1不是极值点.
∴a=3.
5.若函数f(x)=ex-ax-b在R上有小于0的极值点,则实数a的取值范围是( )
A.(-1,0) B.(0,1)
C.(-∞,-1) D.(1,+∞)
B
解析 由题意知f′(x)=ex-a.
当a≤0时,f′(x)>0恒成立,则f(x)在R上单调递增,不符合题意.
当a>0时,令f′(x)=0,解得x=ln a,
∴当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
可知x=ln a为f(x)的极值点,∴ln a<0,∴a∈(0,1).故选B.
6.函数f(x)=ax3+bx在x=1处有极值-2,则a,b的值分别为a=________,b=________.
1
-3
解析 ∵f′(x)=3ax2+b,又当x=1时有极值-2,
∴f′(1)=3a+b=0,①
a+b=-2,②
7.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值又有极小值,则实数a的取值范围是______________________.
(-∞,-1)∪(2,+∞)
解析 f′(x)=3x2+6ax+3(a+2),
令f′(x)=0,即x2+2ax+a+2=0,
∵函数f(x)有极大值和极小值,
∴方程x2+2ax+a+2=0有两个不相等的实数根,即Δ=4a2-4a-8>0,解得a>2或a<-1.
8.函数f(x)=ax-1-ln x(a≤0)在定义域内的极值点的个数为________.
0
所以函数f(x)在(0,+∞)上单调递减,
所以f(x)在(0,+∞)上没有极值点.
由上表可以看出:
当x=-1时,函数有极小值,且极小值为f(-1)=-3;
当x=1时,函数有极大值,且极大值为f(1)=-1.
10.设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
当x∈(0,1)∪(2,+∞)时,f′(x)<0;
当x∈(1,2)时,f′(x)>0;
所以,x=1是函数f(x)的极小值点,
x=2是函数f(x)的极大值点.
A
由题意可得f′(3)=2×9-15a+3a2=0,
整理得a2-5a+6=0,解得a=2或a=3.
当a=2时,f′(x)=2x2-10x+12=2(x-2)(x-3),
令f′(x)>0,得x<2或x>3;令f′(x)<0,得2此时,函数y=f(x)在x=3处取得极小值,不符合题意;
当a=3时,
f′(x)=2x2-15x+27=(x-3)(2x-9).
此时,函数y=f(x)在x=3处取得极大值,符合题意.
综上所述,a=3.
12.若函数f(x)=x3+x2-ax-4在区间(-1,1)上恰有一个极值点,则实数a的取值范围为________.
[1,5)
解析 ∵f′(x)=3x2+2x-a,
函数f(x)在区间(-1,1)上恰有一个极值点,
即f′(x)=0在(-1,1)内恰有一个根.
令f′(x)=0,得x=1或x=-1(舍去).
当x∈(0,1)时,f′(x)<0,因此函数f(x)在(0,1)上是减函数;
当x∈(1,+∞)时,f′(x)>0,因此函数f(x)在(1,+∞)上是增函数.
所以在区间[1,+∞)上,F(x)≤F(1)<0,
即F(x)<0恒成立,
即f(x)因此,当a=1时,在区间[1,+∞)上,函数f(x)的图象在函数g(x)的图象的下方.
14.已知函数f(x)=ax3+bx2+cx的图象如图所示,且f(x)在x=x0与x=2处取得极值,则f(1)+f(-1)的值一定( )
B
A.等于0 B.大于0 C.小于0 D.小于或等于0
解析 f′(x)=3ax2+2bx+c.
令f′(x)=0,则x0和2是该方程的根.
由题图知,f′(x)<0的解集为(x0,2),∴3a>0,则b>0.
∵f(1)+f(-1)=2b,∴f(1)+f(-1)>0.
本课结束
第5章 导数及其应用
5.3.2 极大值与极小值
课标要求
1.借助函数的图象,了解函数在某点取得极值的必要条件和充分条件.2.能利用导数求某些函数的极大值、极小值.
素养要求
通过理解函数的极值及其应用导数求极值的过程,发展学生的直观想象与数学运算素养.
问题导学预习教材
必备知识探究
内容
索引
互动合作研析题型
关键能力提升
拓展延伸分层精练
核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
1
一、函数极大(小)值的概念
1.思考 (1)如图是某处群山的截面图,你能指出山峰、山谷吗?
提示 在x1,x3,x5处是山峰,在x2,x4处是山谷.
(2)你能描述一下在各个山峰、山谷附近的特点吗?
提示 以山峰x=x1处为例来研究,在x=x1处,它附近的函数值都比它小,且在x=x1处的左侧函数是单调递增的,且有f′(x)>0,在x=x1处的右侧函数是单调递减的,且有f′(x)<0,函数图象是连续不断的,f′(x)的变化也是连续不断的,并且有f′(x1)=0.
2.填空 一般地,若存在δ>0,当x∈(x1-δ,x1+δ)时,都有_______________,则称f(x1)为函数f(x)的一个极大值;类似地,若存在δ>0,当x∈(x2-δ,x2+δ)时,都有_________________,则称f(x2)为函数f(x)的一个极小值.
函数的极大值、极小值统称为函数的______.
f(x) ≤f(x1)
f(x)≥f(x2)
极值
温馨提醒 (1)极值是一个局部性概念.由极值的定义知,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个定义域内最大或最小,即反映的是函数在某一点附近的大小情况.
(2)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.
3.做一做 已知函数f(x)的导函数f′(x)的图象如图所示,则函数f(x)有( )
C
A.两个极大值,一个极小值
B.两个极大值,无极小值
C.一个极大值,一个极小值
D.一个极大值,两个极小值
解析 由图可知导函数f′(x)有三个零点,依次设为x1<0,x2=0,x3>0,当x
二、函数的极值与导数的关系
1.思考 导数为0的点一定是极值点吗?
提示 不一定.反例:f(x)=x3,f′(x)=3x2,f′(0)=0,但x=0不是f(x)=x3的极值点.
2.填空 (1)极大值与导数之间的关系
>
=
<
(2)极小值与导数之间的关系
<
=
>
温馨提醒 函数的极值是函数的局部性质,可导函数f(x)在点x=x0处取得极值的充要条件是f′(x0)=0且在x=x0两侧f′(x)符号相反.
-3
解析 f′(x)=x2-2x-3,
令f′(x)>0,得x<-1或x>3,
令f′(x)<0得-1
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
2
角度1 不含参数的函数求极值
例1 求下列函数的极值:
题型一 求函数的极值
(1)f(x)=(x3-1)2+1;
解 ∵f(x)=(x3-1)2+1=x6-2x3+2,
∴f(x)的定义域为R,
f′(x)=6x5-6x2=6x2(x3-1).
令f′(x)=0,得x=0或x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x (0,1) 1 (1,+∞)
f′(x) - 0 +
f(x) ? 3 ?
求可导函数f(x)的极值的步骤
(1)确定函数的定义域,求导数f′(x);
(2)求方程f′(x)=0的根;
(3)用函数的导数为0的点,顺次将函数的定义域分成若干个小开区间,并列成表格.检测f′(x)在方程根左右两侧的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值.
思维升华
训练1 求函数f(x)=x2e-x的极值.
解 函数f(x)的定义域为R,
f′(x)=2xe-x+x2·e-x·(-x)′=2xe-x-x2e-x=x(2-x)e-x.
令f′(x)=0,得x(2-x)e-x=0,解得x=0或x=2.
当x变化时,f′(x),f(x)的变化情况如下表:
因此当x=0时,f(x)取得极小值,且极小值为f(0)=0;
角度2 含参数的函数求极值
解 f′(x)=[x2+(a+2)x-2a2+4a]ex.
令f′(x)=0,解得x=-2a或x=a-2,
当x变化时,f′(x),f(x)的变化情况如下表:
要掌握函数极值的求法,需注意:
导数值为0的点将整个定义域分为若干个区间,可将x,f′(x),f(x)在每个区间内的变化情况列在一个表格中,通过表格可以判断在哪个点处取得极值,是极大值还是极小值.如下两表:
思维升华
由表格可清晰地看出极值的分布情况,对于初学者是首选;后期对求导比较熟练时也可以省去列表格.
训练2 已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
②当a>0时,由f′(x)=0,解得x=a;
∵x∈(0,a)时,f′(x)<0,x∈(a,+∞)时,f′(x)>0,
∴f(x)在x=a处取得极小值,且极小值为f(a)=a-aln a,无极大值.
综上,当a≤0时,函数f(x)无极值;当a>0时,函数f(x)在x=a处取得极小值a-aln a,无极大值.
例3 已知函数f(x)=ax3+bx2+cx(a≠0)在x=±1处取得极值,且f(1)=-1.
(1)求常数a,b,c的值;
题型二 利用函数极值确定参数的值
解 f′(x)=3ax2+2bx+c.
∵x=±1是函数f(x)的极值点,
∴x=±1是方程f′(x)=3ax2+2bx+c=0的两根,
又f(1)=-1,
∴a+b+c=-1. ③
(2)判断x=±1是函数的极大值点还是极小值点,试说明理由,并求出极值.
当x<-1或x>1时,f′(x)>0,
当-1
∴当x=-1时,函数取得极大值f(-1)=1,
当x=1时,函数取得极小值f(1)=-1.
已知函数极值,确定函数解析式中的参数时,注意两点
(1)根据极值点的导数为0和极值这两个条件列方程组,利用待定系数法求解;
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证充分性.
思维升华
训练3 已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,求常数a,b的值.
当a=1,b=3时,
f′(x)=3x2+6x+3=3(x+1)2≥0,
所以f(x)在R上为增函数,无极值,故舍去.
当a=2,b=9时,f′(x)=3x2+12x+9=3(x+1)(x+3).
当x∈(-3,-1)时,f′(x)<0,f(x)为减函数;
当x∈(-∞,-3)和(-1,+∞)时,f′(x)>0,f(x)为增函数,
所以f(x)在x=-1时取得极小值,因此a=2,b=9.
题型三 极值的综合应用
例4 已知函数f(x)=x3-3x+a(a为实数),若方程f(x)=0有三个不同实根,求实数a的取值范围.
解 令f′(x)=3x2-3=3(x+1)(x-1)=0,
解得x1=-1,x2=1.
当x<-1时,f′(x)>0;
当-1
所以当x=-1时,
f(x)有极大值f(-1)=2+a;
当x=1时,f(x)有极小值f(1)=-2+a.
因为方程f(x)=0有三个不同实根,
所以y=f(x)的图象与x轴有三个交点,如图.
迁移1 (改变条件)本例中,若方程f(x)=0恰有两个根,则实数a的值如何求解?
解 由例题,知函数的极大值f(-1)=2+a,极小值f(1)=-2+a,
若f(x)=0恰有两个根,则有2+a=0,或-2+a=0,
所以a=-2或a=2.
迁移2 本例中,若方程f(x)=0有且只有一个实根,求实数a的取值范围.
解 由例题可知,要使方程f(x)=0有且只有一个实根,
只需2+a<0或-2+a>0,即a<-2或a>2.故a的取值范围为
(-∞,-2)∪(2,+∞).
利用导数可以判断函数的单调性,研究函数的极值情况,并能在此基础上画出函数的大致图象,从直观上判断函数图象与x轴的交点或两个函数图象的交点个数,从而为研究方程根的个数问题提供了方便.
思维升华
(2)若函数y=f(x)-m仅有一个零点,求实数m的取值范围.
解 由(1),知当x>0时,f(x)=(x2-2x)ex,f′(x)=(x2-2)ex.
课堂小结
1.牢记2个知识点
(1)极值的概念.
(2)极值与导数的关系.
2.掌握2种方法
(1)求极值的方法.
(2)已知极值求函数解析式的方法.
3.注意1个易错点
对极值的充要条件把握不准致错.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
3
1.下列函数中存在极值的是( )
B
解析 对于y=x-ex,y′=1-ex,x∈R,
令y′=0,得x=0.
在区间(-∞,0)上,y′>0;
在区间(0,+∞)上,y′<0.
故x=0为函数y=x-ex的极大值点.
2.函数f(x)=(x-1)ex的极小值点为( )
A.(0,-1) B.(0,0)
C.-1 D.0
D
解析 由题意得f′(x)=ex+(x-1)ex=xex,x∈R,故f(x)在(-∞,0)上是减函数,在(0,+∞)上是增函数,
故当x=0时,f(x)的极小值为f(0)=-1,故极小值点为0.
3.(多选)定义在R上的可导函数y=f(x)的导函数的图象如图所示,以下结论正确的是( )
ACD
A.-3是f(x)的一个极小值点
B.-2和-1都是f(x)的极大值点
C.f(x)的单调递增区间是(-3,+∞)
D.f(x)的单调递减区间是(-∞,-3)
解析 当x<-3时,f′(x)<0,x∈(-3,+∞)时f′(x)≥0,∴-3是极小值点,无极大值点,增区间是(-3,+∞),减区间是(-∞,-3).故选ACD.
4.函数f(x)=x3+ax2+bx+a2+a在x=1处有极值为7,则a等于( )
A.-3或3 B.3或-9 C.3 D.-3
C
解析 f′(x)=3x2+2ax+b,
当a=3,b=-9时,f′(x)=3x2+6x-9=3(x-1)(x+3),当-3
当a=-3,b=3时,f′(x)=3x2-6x+3=3(x-1)2≥0,x=1不是极值点.
∴a=3.
5.若函数f(x)=ex-ax-b在R上有小于0的极值点,则实数a的取值范围是( )
A.(-1,0) B.(0,1)
C.(-∞,-1) D.(1,+∞)
B
解析 由题意知f′(x)=ex-a.
当a≤0时,f′(x)>0恒成立,则f(x)在R上单调递增,不符合题意.
当a>0时,令f′(x)=0,解得x=ln a,
∴当x∈(-∞,ln a)时,f′(x)<0;
当x∈(ln a,+∞)时,f′(x)>0.
可知x=ln a为f(x)的极值点,∴ln a<0,∴a∈(0,1).故选B.
6.函数f(x)=ax3+bx在x=1处有极值-2,则a,b的值分别为a=________,b=________.
1
-3
解析 ∵f′(x)=3ax2+b,又当x=1时有极值-2,
∴f′(1)=3a+b=0,①
a+b=-2,②
7.函数f(x)=x3+3ax2+3(a+2)x+3既有极大值又有极小值,则实数a的取值范围是______________________.
(-∞,-1)∪(2,+∞)
解析 f′(x)=3x2+6ax+3(a+2),
令f′(x)=0,即x2+2ax+a+2=0,
∵函数f(x)有极大值和极小值,
∴方程x2+2ax+a+2=0有两个不相等的实数根,即Δ=4a2-4a-8>0,解得a>2或a<-1.
8.函数f(x)=ax-1-ln x(a≤0)在定义域内的极值点的个数为________.
0
所以函数f(x)在(0,+∞)上单调递减,
所以f(x)在(0,+∞)上没有极值点.
由上表可以看出:
当x=-1时,函数有极小值,且极小值为f(-1)=-3;
当x=1时,函数有极大值,且极大值为f(1)=-1.
10.设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
当x∈(0,1)∪(2,+∞)时,f′(x)<0;
当x∈(1,2)时,f′(x)>0;
所以,x=1是函数f(x)的极小值点,
x=2是函数f(x)的极大值点.
A
由题意可得f′(3)=2×9-15a+3a2=0,
整理得a2-5a+6=0,解得a=2或a=3.
当a=2时,f′(x)=2x2-10x+12=2(x-2)(x-3),
令f′(x)>0,得x<2或x>3;令f′(x)<0,得2
当a=3时,
f′(x)=2x2-15x+27=(x-3)(2x-9).
此时,函数y=f(x)在x=3处取得极大值,符合题意.
综上所述,a=3.
12.若函数f(x)=x3+x2-ax-4在区间(-1,1)上恰有一个极值点,则实数a的取值范围为________.
[1,5)
解析 ∵f′(x)=3x2+2x-a,
函数f(x)在区间(-1,1)上恰有一个极值点,
即f′(x)=0在(-1,1)内恰有一个根.
令f′(x)=0,得x=1或x=-1(舍去).
当x∈(0,1)时,f′(x)<0,因此函数f(x)在(0,1)上是减函数;
当x∈(1,+∞)时,f′(x)>0,因此函数f(x)在(1,+∞)上是增函数.
所以在区间[1,+∞)上,F(x)≤F(1)<0,
即F(x)<0恒成立,
即f(x)
14.已知函数f(x)=ax3+bx2+cx的图象如图所示,且f(x)在x=x0与x=2处取得极值,则f(1)+f(-1)的值一定( )
B
A.等于0 B.大于0 C.小于0 D.小于或等于0
解析 f′(x)=3ax2+2bx+c.
令f′(x)=0,则x0和2是该方程的根.
由题图知,f′(x)<0的解集为(x0,2),∴3a>0,则b>0.
∵f(1)+f(-1)=2b,∴f(1)+f(-1)>0.
本课结束
