余角和补角2[上学期]
图片预览




文档简介
课件14张PPT。余角和补角一、复习回顾二、探究新知四、巩固练习三、拓展训练教学过程复习1、周角=______度
2、平角=______度
3、直角=______度
4、平角是一条直线吗?
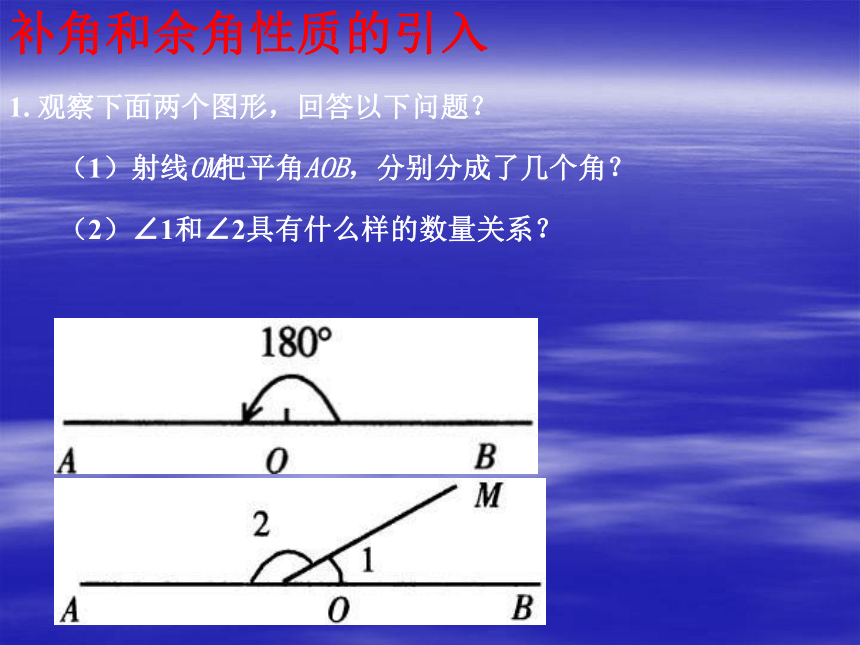
5、周角是一条射线吗?补角和余角性质的引入1. 观察下面两个图形,回答以下问题?(1)射线OM把平角AOB,分别分成了几个角?(2)∠1和∠2具有什么样的数量关系?互为补角
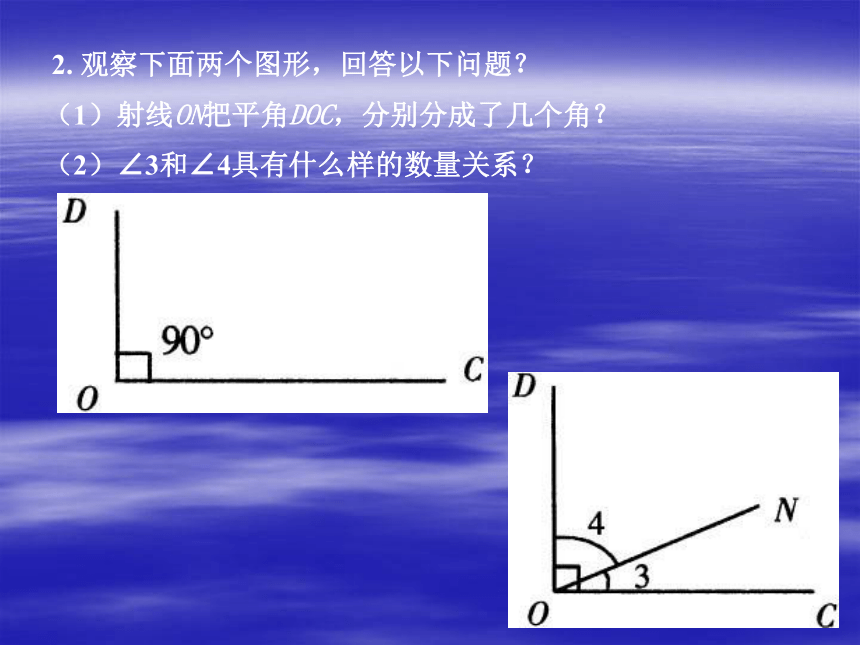
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。2. 观察下面两个图形,回答以下问题?(1)射线ON把平角DOC,分别分成了几个角?(2)∠3和∠4具有什么样的数量关系?互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。问题3:互为余角、互为补角的两个角是否一定有公共顶点? 问题1:以上定义中的“互为”是什么意思?问题2:若 ,那么∠1、∠2、∠3互为补角吗? 练习:如图,O是直线AB上一点,OC是∠AOB的平分线
①∠AOD的补角是____________
②∠AOD的余角是____________
③∠DOB的补角是____________∠DOB∠DOC∠AOD问题:如下图,∠1与∠2互补,∠3与∠4互补,如果
∠1=∠3,那么∠2=∠4成立吗?例1
若一个角的补角等于它的余角的4倍,求这个角的度数。解:设这个角是x °,则它的补角是(180-x) °,余角是(90-x) ° 。
根据题意得:
(180-x) °= 4 (90-x) °
解得: x =60
答:这个角的度数是60 °。例2、如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2AOBCD(同角的余角相等)12练习
一、填空
1、70°39′的余角是 ,补角是 。
2、如果一个角的补角是150 ° ;那么这个角的余角是 。
3、x °(x<90)的余角是 ,它的补角是 。
109 °21 ′19 °21 ′(90-x) ° (180-x) °总结:锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )60 °小结∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。ABCDEFG如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °找出图中相等的角并说明理由。讨论
2、平角=______度
3、直角=______度
4、平角是一条直线吗?
5、周角是一条射线吗?补角和余角性质的引入1. 观察下面两个图形,回答以下问题?(1)射线OM把平角AOB,分别分成了几个角?(2)∠1和∠2具有什么样的数量关系?互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。2. 观察下面两个图形,回答以下问题?(1)射线ON把平角DOC,分别分成了几个角?(2)∠3和∠4具有什么样的数量关系?互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。问题3:互为余角、互为补角的两个角是否一定有公共顶点? 问题1:以上定义中的“互为”是什么意思?问题2:若 ,那么∠1、∠2、∠3互为补角吗? 练习:如图,O是直线AB上一点,OC是∠AOB的平分线
①∠AOD的补角是____________
②∠AOD的余角是____________
③∠DOB的补角是____________∠DOB∠DOC∠AOD问题:如下图,∠1与∠2互补,∠3与∠4互补,如果
∠1=∠3,那么∠2=∠4成立吗?例1
若一个角的补角等于它的余角的4倍,求这个角的度数。解:设这个角是x °,则它的补角是(180-x) °,余角是(90-x) ° 。
根据题意得:
(180-x) °= 4 (90-x) °
解得: x =60
答:这个角的度数是60 °。例2、如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2AOBCD(同角的余角相等)12练习
一、填空
1、70°39′的余角是 ,补角是 。
2、如果一个角的补角是150 ° ;那么这个角的余角是 。
3、x °(x<90)的余角是 ,它的补角是 。
109 °21 ′19 °21 ′(90-x) ° (180-x) °总结:锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )60 °小结∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。ABCDEFG如图,E、F是直线DG上两点
∠BEF = ∠BFE
∠AED = ∠CFG = 90 °找出图中相等的角并说明理由。讨论
