华师大数学七年级上第5章 相交线与平行线 单元评价检测(试题+解析)
文档属性
| 名称 | 华师大数学七年级上第5章 相交线与平行线 单元评价检测(试题+解析) |  | |
| 格式 | zip | ||
| 文件大小 | 135.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-04 11:30:58 | ||
图片预览


文档简介
单元评价检测(四)
第5章
(45分钟100分)
一、选择题(每小题4分,共28分)
1.(2013·枣庄中考)如图,AB∥CD,∠CDE=140°,则∠A的度数为 ( )
( http: / / www.21cnjy.com )
A.140° B.60°
C.50° D.40°
【解析】选D.∠ADC=180°-∠CDE =40°,
∵AB∥CD,∴∠ADC=∠A=40°.
2.如图,在△ABC中,D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的 ( )
A.∠1=∠2 B.∠2=∠AFD
C.∠1=∠AFD D.∠1=∠DFE
【解析】选D.∵EF∥AB,
∴∠1=∠2(两直线平行,同位角相等).
∵∠1=∠DFE,∴∠2=∠DFE(等量代换),
∴DF∥BC(内错角相等,两直线平行).
所以只需满足∠1=∠DFE.
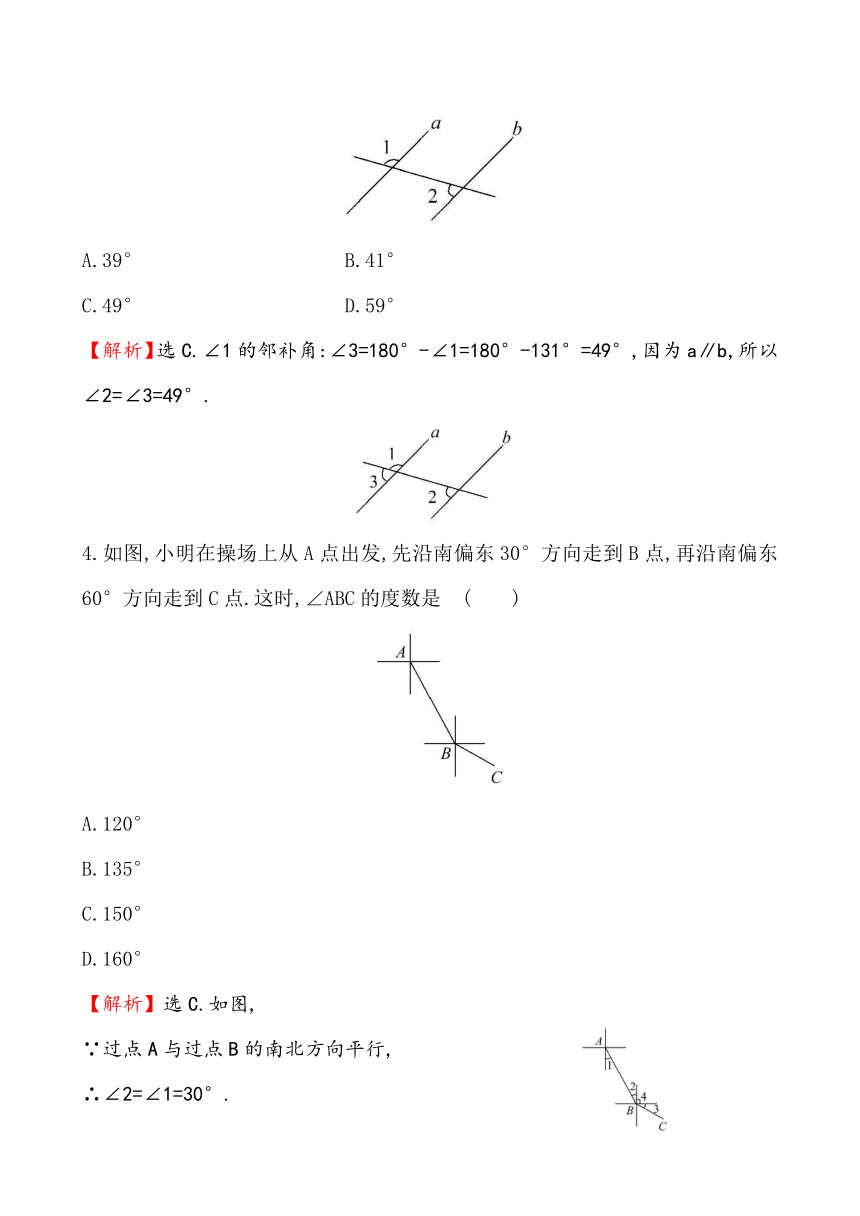
3.(2013·乐山中考)如图,已知直线a∥b,∠1=131°,则∠2等于 ( )
( http: / / www.21cnjy.com )
A.39° B.41°
C.49° D.59°
【解析】选C.∠1的邻补角:∠3=180°-∠1=180°-131°=49°,因为a∥b,所以∠2=∠3=49°.
( http: / / www.21cnjy.com )
4.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点.这时,∠ABC的度数是 ( )
( http: / / www.21cnjy.com )
A.120°
B.135°
C.150°
D.160°
【解析】选C.如图,
∵过点A与过点B的南北方向平行,
∴∠2=∠1=30°.
∵∠4=90°,∴∠ABC=30°+90°+30°=150°.
5.(2013·重庆中考)如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为 ( )
( http: / / www.21cnjy.com )
A.40° B.35°
C.50° D.45°
【解析】选A.∵AD平分∠BAC,∴∠BAC=2∠BAD.∵∠BAD=70°,∴∠BAC=140°.
∵AB∥CD,∴∠ACD+∠BAC=180°,
∴∠ACD=180°-∠BAC=40°.
6.已知:直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于 ( )
( http: / / www.21cnjy.com )
A.30° B.35°
C.40° D.45°
【解析】选B.过60°角的顶点作l3∥l1,则l3∥l2,
( http: / / www.21cnjy.com )
∴∠2=∠3,∠5=∠4,
∴∠2+∠5=∠3+∠4=60°,
∵∠5=∠1=25°,∴∠2=35°.
7.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为 ( )
( http: / / www.21cnjy.com )
A.68° B.34°
C.56° D.不能确定
【解析】选A.∵AD∥BC,∴∠DEF=∠1=56°,
∵长方形纸条ABCD沿EF折叠,
∴∠GEF=∠DEF=56°,∴∠DEG=112°.
∵AD∥BC,∴∠EGF+∠DEG=180°,
∴∠EGF=180°-∠DEG=180°-112°=68°.
二、填空题(每小题5分,共25分)
8.如图,∠1=∠2,∠B+∠BDE=180°,则图中一组平行线可以是 .
【解析】∵∠1=∠2,
∴AB∥EF(内错角相等,两直线平行).
∵∠B+∠BDE=180°,∴DE∥BC(同旁内角互补,两直线平行).
答案:AB∥EF或DE∥BC(填一个即可)
9.(2013·玉溪中考)如图,AB∥CD,∠BAF=115°,则∠ECF的度数为 .
【解析】因为AB∥CD,所以∠BAF=∠DCF=115°,所以∠ECF=180°-115°=65°.
答案:65°
10.(2013·淮安中考)如图,三角板的直角顶点在直线l上,若∠1=40°,则∠2= .
( http: / / www.21cnjy.com )
【解析】∵∠1+∠2+90°=180°,∴∠1+∠2=90°.
∴∠2=90°-40°=50°.
答案:50°
11.如图,已知EF⊥AB于E,CD是过E的直线,且∠AEC=120°,则∠DEF= .
( http: / / www.21cnjy.com )
【解析】利用垂直的定义和对顶角的性质,
∵∠AEC和∠DEB是对顶角,
∴∠DEB=∠AEC=120°.
又∵EF⊥AB,∠BEF=90°,
∴∠DEF=120°-90°=30°.
答案:30°
12.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
【解析】过B作BF∥AE,
( http: / / www.21cnjy.com )
则CD∥BF∥AE,∴∠BCD+∠1=180°.
又∵AB⊥AE,∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
答案:270
三、解答题(共47分)
13.(12分)如图,已知AB∥CD,EF⊥AB,GF交AB于点Q,∠GQA=50°,求∠EFG的度数.
【解析】∵AB∥CD,EF⊥AB,
∴EF⊥CD,∴∠EFC=90°,
∵AB∥CD,∴∠GFC=∠GQA=50°,
∴∠EFG=∠EFC-∠GFC=40°.
14.(10分)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
【解析】∵AB∥CD,∠A=37°,
∴∠ECD=∠A=37°.∵DE⊥AE,
∴∠D=90°-∠ECD=90°-37°=53°.
15.(12分)如图,如果∠1=∠2,∠C=∠D,那么∠A=∠F吗 为什么
( http: / / www.21cnjy.com )
【解析】∵∠1=∠2,∠2=∠3,∴∠1=∠3,
∴BD∥CE,∴∠4=∠C.
又∵∠C=∠D,∴∠4=∠D,∴DF∥CA.∴∠A=∠F.
16.(13分)如图,已知DB∥FG∥EC,∠ABD=84°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.
【解析】∵DB∥FG∥EC,
∴∠BAG=∠ABD=84°,∠GAC=∠ACE=60°;
∴∠BAC=∠BAG+∠GAC=144°,
∵AP是∠BAC的平分线,
∴∠PAC=∠BAC=72°,
∴∠PAG=∠PAC-∠GAC=72°-60°=12°.
第5章
(45分钟100分)
一、选择题(每小题4分,共28分)
1.(2013·枣庄中考)如图,AB∥CD,∠CDE=140°,则∠A的度数为 ( )
( http: / / www.21cnjy.com )
A.140° B.60°
C.50° D.40°
【解析】选D.∠ADC=180°-∠CDE =40°,
∵AB∥CD,∴∠ADC=∠A=40°.
2.如图,在△ABC中,D,E,F分别在AB,BC,AC上,且EF∥AB,要使DF∥BC,只需满足下列条件中的 ( )
A.∠1=∠2 B.∠2=∠AFD
C.∠1=∠AFD D.∠1=∠DFE
【解析】选D.∵EF∥AB,
∴∠1=∠2(两直线平行,同位角相等).
∵∠1=∠DFE,∴∠2=∠DFE(等量代换),
∴DF∥BC(内错角相等,两直线平行).
所以只需满足∠1=∠DFE.
3.(2013·乐山中考)如图,已知直线a∥b,∠1=131°,则∠2等于 ( )
( http: / / www.21cnjy.com )
A.39° B.41°
C.49° D.59°
【解析】选C.∠1的邻补角:∠3=180°-∠1=180°-131°=49°,因为a∥b,所以∠2=∠3=49°.
( http: / / www.21cnjy.com )
4.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点.这时,∠ABC的度数是 ( )
( http: / / www.21cnjy.com )
A.120°
B.135°
C.150°
D.160°
【解析】选C.如图,
∵过点A与过点B的南北方向平行,
∴∠2=∠1=30°.
∵∠4=90°,∴∠ABC=30°+90°+30°=150°.
5.(2013·重庆中考)如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为 ( )
( http: / / www.21cnjy.com )
A.40° B.35°
C.50° D.45°
【解析】选A.∵AD平分∠BAC,∴∠BAC=2∠BAD.∵∠BAD=70°,∴∠BAC=140°.
∵AB∥CD,∴∠ACD+∠BAC=180°,
∴∠ACD=180°-∠BAC=40°.
6.已知:直线l1∥l2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于 ( )
( http: / / www.21cnjy.com )
A.30° B.35°
C.40° D.45°
【解析】选B.过60°角的顶点作l3∥l1,则l3∥l2,
( http: / / www.21cnjy.com )
∴∠2=∠3,∠5=∠4,
∴∠2+∠5=∠3+∠4=60°,
∵∠5=∠1=25°,∴∠2=35°.
7.如图,把一张长方形纸条ABCD沿EF折叠,若∠1=56°,则∠EGF应为 ( )
( http: / / www.21cnjy.com )
A.68° B.34°
C.56° D.不能确定
【解析】选A.∵AD∥BC,∴∠DEF=∠1=56°,
∵长方形纸条ABCD沿EF折叠,
∴∠GEF=∠DEF=56°,∴∠DEG=112°.
∵AD∥BC,∴∠EGF+∠DEG=180°,
∴∠EGF=180°-∠DEG=180°-112°=68°.
二、填空题(每小题5分,共25分)
8.如图,∠1=∠2,∠B+∠BDE=180°,则图中一组平行线可以是 .
【解析】∵∠1=∠2,
∴AB∥EF(内错角相等,两直线平行).
∵∠B+∠BDE=180°,∴DE∥BC(同旁内角互补,两直线平行).
答案:AB∥EF或DE∥BC(填一个即可)
9.(2013·玉溪中考)如图,AB∥CD,∠BAF=115°,则∠ECF的度数为 .
【解析】因为AB∥CD,所以∠BAF=∠DCF=115°,所以∠ECF=180°-115°=65°.
答案:65°
10.(2013·淮安中考)如图,三角板的直角顶点在直线l上,若∠1=40°,则∠2= .
( http: / / www.21cnjy.com )
【解析】∵∠1+∠2+90°=180°,∴∠1+∠2=90°.
∴∠2=90°-40°=50°.
答案:50°
11.如图,已知EF⊥AB于E,CD是过E的直线,且∠AEC=120°,则∠DEF= .
( http: / / www.21cnjy.com )
【解析】利用垂直的定义和对顶角的性质,
∵∠AEC和∠DEB是对顶角,
∴∠DEB=∠AEC=120°.
又∵EF⊥AB,∠BEF=90°,
∴∠DEF=120°-90°=30°.
答案:30°
12.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
【解析】过B作BF∥AE,
( http: / / www.21cnjy.com )
则CD∥BF∥AE,∴∠BCD+∠1=180°.
又∵AB⊥AE,∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
答案:270
三、解答题(共47分)
13.(12分)如图,已知AB∥CD,EF⊥AB,GF交AB于点Q,∠GQA=50°,求∠EFG的度数.
【解析】∵AB∥CD,EF⊥AB,
∴EF⊥CD,∴∠EFC=90°,
∵AB∥CD,∴∠GFC=∠GQA=50°,
∴∠EFG=∠EFC-∠GFC=40°.
14.(10分)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°,求∠D的度数.
【解析】∵AB∥CD,∠A=37°,
∴∠ECD=∠A=37°.∵DE⊥AE,
∴∠D=90°-∠ECD=90°-37°=53°.
15.(12分)如图,如果∠1=∠2,∠C=∠D,那么∠A=∠F吗 为什么
( http: / / www.21cnjy.com )
【解析】∵∠1=∠2,∠2=∠3,∴∠1=∠3,
∴BD∥CE,∴∠4=∠C.
又∵∠C=∠D,∴∠4=∠D,∴DF∥CA.∴∠A=∠F.
16.(13分)如图,已知DB∥FG∥EC,∠ABD=84°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.
【解析】∵DB∥FG∥EC,
∴∠BAG=∠ABD=84°,∠GAC=∠ACE=60°;
∴∠BAC=∠BAG+∠GAC=144°,
∵AP是∠BAC的平分线,
∴∠PAC=∠BAC=72°,
∴∠PAG=∠PAC-∠GAC=72°-60°=12°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
