余角与补角[上学期]
图片预览





文档简介
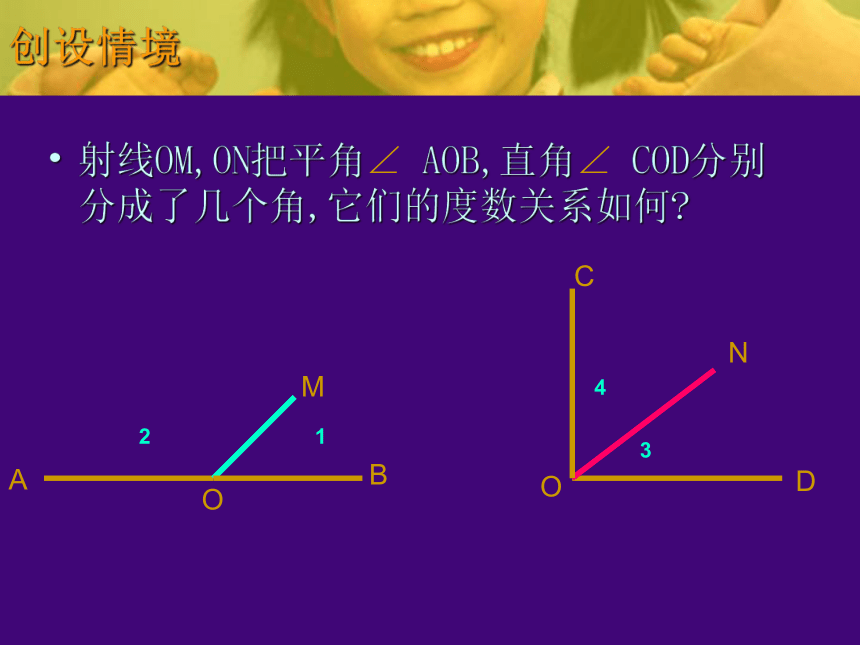
课件14张PPT。 龙坪中心学校数学组余角和补角创设情境射线OM,ON把平角∠ AOB,直角∠ COD分别分成了几个角,它们的度数关系如何?3412MOBAODCN学习新知如图,如果两个角的和等于90 ° (直角),
就说这两个角互为余角,即其中每个
角是另一个角的余角.
∠ 3+ ∠ 4=90 °类似地,如图,如果两个角的和等于
180 °(平角),就说这两个角互为补角,
即其中一个角是另一个角的补角.
∠ 1+ ∠ 2=180 °注意:1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。练一练练习1:
1.若∠ 1与∠ 2互补,
则∠ 1+ ∠ 2= ;
2.若∠ 3与∠ 4互余,
则∠ 3+ ∠ 4= ;
3.30°角的余角为 ,补角为 ,
70 °39′的余角为 ,补角为 .
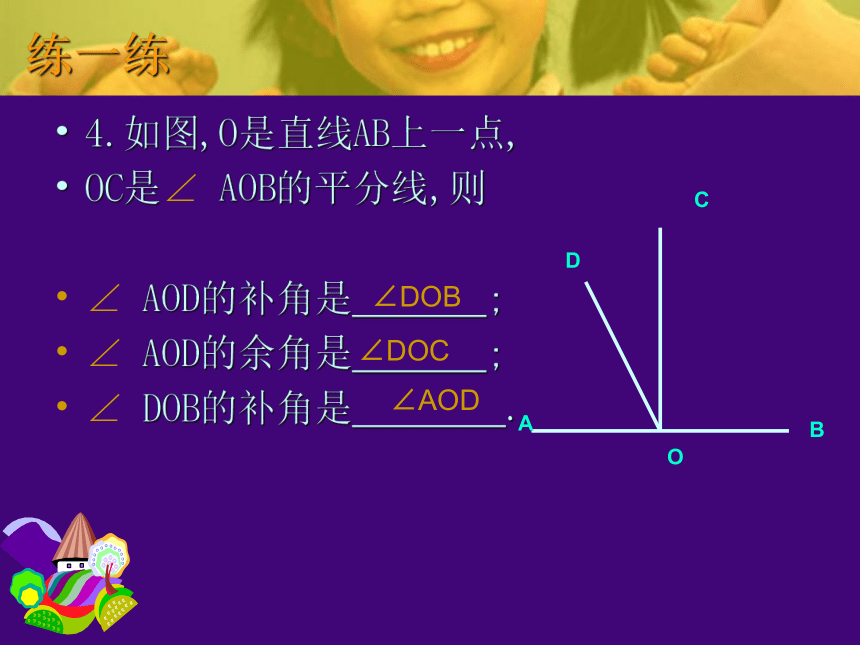
180 °90 °60 °150 °19 °21 ′ 109 °21 ′练一练4.如图,O是直线AB上一点,
OC是∠ AOB的平分线,则
∠ AOD的补角是 ;
∠ AOD的余角是 ;
∠ DOB的补角是 .
∠DOB∠DOC∠AOD练习2:(1)如果∠ 的余角是∠ 的2 倍,求 ∠ 的度数。解:设∠ 的度数为x度,则 ∠ 的余角为(90-x)度。由题意,得: 90-x=2 x-3x=-90
x=30 答:∠ 的度数为30度。(2)如果∠1的补角是∠1的3倍,求∠1的度数。解:设∠1的度数为x度,则 ∠1的补角(180-x)度。由题意得: 180-x=3x -4x=-180
x=45 答:∠1为45°.学习新知例1.如图, ∠ 1与∠ 2互补, ∠ 3与∠ 4互补,若
∠ 1= ∠ 3,那么∠ 2与∠ 4相等吗?为什么?解:∵ ∠ 1与∠ 2互补 ,
∴∠ 1+ ∠ 2=180 °,即∠ 2=180 ° - ∠ 1.
又∵∠ 3与∠ 4互补,
∴∠ 3+ ∠ 4=180 °,即∠ 4=180 ° - ∠ 3.
∵∠ 1= ∠ 3
∴∠ 2= ∠ 4通过以上题目,你是否发现了两个等角的补角间的关系?你能试着总结吗?①若∠ =∠同角或等角的补角相等。即∠ 的补角= ∠ 的补角②若∠ =∠即∠ 的余角= ∠ 的余角同角或等角的余角相等。想一想?本节课我们研究了以下内容:
1 余角和补角的定义:如果 两个角的和等于90度,就说这两个角互为余角;如果两个角的和等于180度就说这两个角互为补角.
2 余角和补角的性质:同角或等角的补角相等;同角或等角的余角相等.小结∠ 的余角=90°- ∠ ∠ 的余角=90°- ∠若∠ = ∠ 则90°- ∠ =90°- ∠即∠ 的余角= ∠ 的余角 具体的说 :
(1)余角的 性质:同角或等角的余角相等。图形一(2)补角的 性质:∠ 的补角= 180o -∠∠ 的补角= 180o -∠若∠ =∠即∠ 的补角= ∠ 的补角同角或等角的补角相等。图形2课堂作业P139页 X5, 6
就说这两个角互为余角,即其中每个
角是另一个角的余角.
∠ 3+ ∠ 4=90 °类似地,如图,如果两个角的和等于
180 °(平角),就说这两个角互为补角,
即其中一个角是另一个角的补角.
∠ 1+ ∠ 2=180 °注意:1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。练一练练习1:
1.若∠ 1与∠ 2互补,
则∠ 1+ ∠ 2= ;
2.若∠ 3与∠ 4互余,
则∠ 3+ ∠ 4= ;
3.30°角的余角为 ,补角为 ,
70 °39′的余角为 ,补角为 .
180 °90 °60 °150 °19 °21 ′ 109 °21 ′练一练4.如图,O是直线AB上一点,
OC是∠ AOB的平分线,则
∠ AOD的补角是 ;
∠ AOD的余角是 ;
∠ DOB的补角是 .
∠DOB∠DOC∠AOD练习2:(1)如果∠ 的余角是∠ 的2 倍,求 ∠ 的度数。解:设∠ 的度数为x度,则 ∠ 的余角为(90-x)度。由题意,得: 90-x=2 x-3x=-90
x=30 答:∠ 的度数为30度。(2)如果∠1的补角是∠1的3倍,求∠1的度数。解:设∠1的度数为x度,则 ∠1的补角(180-x)度。由题意得: 180-x=3x -4x=-180
x=45 答:∠1为45°.学习新知例1.如图, ∠ 1与∠ 2互补, ∠ 3与∠ 4互补,若
∠ 1= ∠ 3,那么∠ 2与∠ 4相等吗?为什么?解:∵ ∠ 1与∠ 2互补 ,
∴∠ 1+ ∠ 2=180 °,即∠ 2=180 ° - ∠ 1.
又∵∠ 3与∠ 4互补,
∴∠ 3+ ∠ 4=180 °,即∠ 4=180 ° - ∠ 3.
∵∠ 1= ∠ 3
∴∠ 2= ∠ 4通过以上题目,你是否发现了两个等角的补角间的关系?你能试着总结吗?①若∠ =∠同角或等角的补角相等。即∠ 的补角= ∠ 的补角②若∠ =∠即∠ 的余角= ∠ 的余角同角或等角的余角相等。想一想?本节课我们研究了以下内容:
1 余角和补角的定义:如果 两个角的和等于90度,就说这两个角互为余角;如果两个角的和等于180度就说这两个角互为补角.
2 余角和补角的性质:同角或等角的补角相等;同角或等角的余角相等.小结∠ 的余角=90°- ∠ ∠ 的余角=90°- ∠若∠ = ∠ 则90°- ∠ =90°- ∠即∠ 的余角= ∠ 的余角 具体的说 :
(1)余角的 性质:同角或等角的余角相等。图形一(2)补角的 性质:∠ 的补角= 180o -∠∠ 的补角= 180o -∠若∠ =∠即∠ 的补角= ∠ 的补角同角或等角的补角相等。图形2课堂作业P139页 X5, 6
