3.1等式的性质[上学期]
文档属性
| 名称 | 3.1等式的性质[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 29.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-31 00:00:00 | ||
图片预览







文档简介
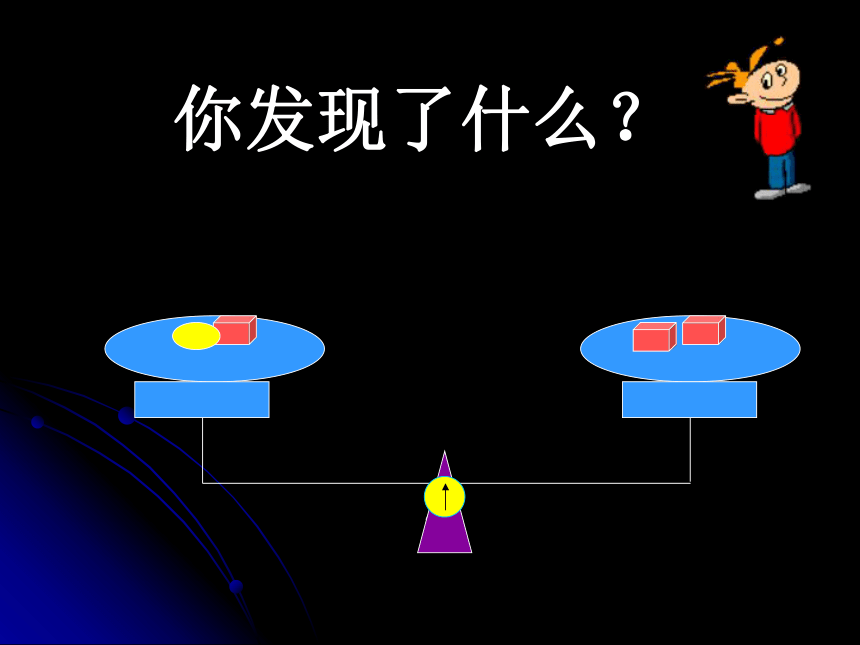
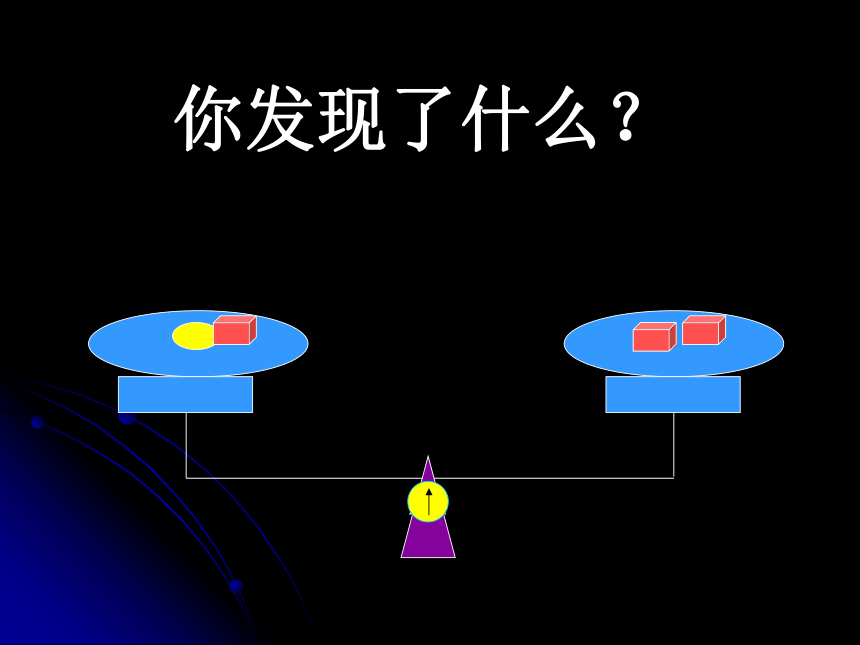
课件20张PPT。2.1.2等式的性质(1)估计方程的解:你发现了什么?你发现了什么?等式性质1:等式两边加(或减)同一个数(或式子),结果仍是等式例题1:解方程: x–7=5x=?两边同加上7分析:解方程: x–7=5解:方程两边都加上7,得 x–7+7=5+7即:
x=5+7
x=12检验:把x=12代入原方程得, 左边=12–7=5,右边=5 左边=右边 ∴x=12是原方程的解。 检验:方程的两边都代入x=12,得 左边=12–7=5, 右边=5 左边=右边 所以x=12是原方程的解。 解: x –7 = 5 x = 5 +7
x = 12把方程中某一项改变符号后,从方程的一边移到另一边,这种变形叫移 项从左移右改变符号例题2:解方程: 7x=6x–4x=?两边同减去6x分析:解方程:7x=6x–4 两边同减去6x,得 7x–6x=6x–4-6x合并同类项,得
x =–4 检验: 把x=–4代入原方程得, 左边=7x(–4)=-28,
右边=6x(–4)–4=–28
左边=右边
∴ x=–4是原方程的解解:解方程:7x=6x–4 7x –6x=–4
从右移左改变符号注意:
x =–4 (1)移项要变号 (2)将含未知数项移到方程的一边(一般为左边),而将常数项移到方程的另一边(一般为右边) (3)解方程不要连等例:通过移项解下列方程,并写出检验
(1) 3x=2x+5 (2) 7x–3=6x-2 (1) 3x=2x+5 解:3x–2x=5
合并同类项,得
x=5
把x=5代入方程的两边,得
左边=3×5=15,右边=2×5+5=15
左边=右边
∴ x=5是原方程的解。
移项,得检验:
(2) 7x–3=6x-2
解:移项,得
7x–6x=-2+3
合并同类项,得x=1
检验:把x=1代入方程的两边,得
左边=7×1–3=4,右边=6×1-2=4
左边=右边
∴ x=1是原方程的解练习:下面的移项对不对?如果不对,错在哪里?应当怎样改正?
(1)从7+x=13,得到x=13+7 (2)从5x=4x+8,得到5x–4x=8 (3)从3x=8-2x,得3x+2x=-8 χ改:从7+x=13,得到x=13–7? χ 改:从3x=8-2x 得 3x+2x=8巩固练习:练习:小明在解方程x–4=7时,是这样写解的过程的:
x–4=7=x=7+4=x=11
(1)小明这样写对不对?
(2)应该怎样写?× 解:x–4=7
移项,得
x=7+4
合并同类项,得
x=11练习2、解下列方程,并写出检验过程 (1)x+11=38 (2)7+x=5 (3)12x-1=11x (4)9+11x=10x-7巩固练习:本节小结本节课我们学习了什么知识?
移项的依据是什么?移项应该注意什么?作业:作业本(2)
x=5+7
x=12检验:把x=12代入原方程得, 左边=12–7=5,右边=5 左边=右边 ∴x=12是原方程的解。 检验:方程的两边都代入x=12,得 左边=12–7=5, 右边=5 左边=右边 所以x=12是原方程的解。 解: x –7 = 5 x = 5 +7
x = 12把方程中某一项改变符号后,从方程的一边移到另一边,这种变形叫移 项从左移右改变符号例题2:解方程: 7x=6x–4x=?两边同减去6x分析:解方程:7x=6x–4 两边同减去6x,得 7x–6x=6x–4-6x合并同类项,得
x =–4 检验: 把x=–4代入原方程得, 左边=7x(–4)=-28,
右边=6x(–4)–4=–28
左边=右边
∴ x=–4是原方程的解解:解方程:7x=6x–4 7x –6x=–4
从右移左改变符号注意:
x =–4 (1)移项要变号 (2)将含未知数项移到方程的一边(一般为左边),而将常数项移到方程的另一边(一般为右边) (3)解方程不要连等例:通过移项解下列方程,并写出检验
(1) 3x=2x+5 (2) 7x–3=6x-2 (1) 3x=2x+5 解:3x–2x=5
合并同类项,得
x=5
把x=5代入方程的两边,得
左边=3×5=15,右边=2×5+5=15
左边=右边
∴ x=5是原方程的解。
移项,得检验:
(2) 7x–3=6x-2
解:移项,得
7x–6x=-2+3
合并同类项,得x=1
检验:把x=1代入方程的两边,得
左边=7×1–3=4,右边=6×1-2=4
左边=右边
∴ x=1是原方程的解练习:下面的移项对不对?如果不对,错在哪里?应当怎样改正?
(1)从7+x=13,得到x=13+7 (2)从5x=4x+8,得到5x–4x=8 (3)从3x=8-2x,得3x+2x=-8 χ改:从7+x=13,得到x=13–7? χ 改:从3x=8-2x 得 3x+2x=8巩固练习:练习:小明在解方程x–4=7时,是这样写解的过程的:
x–4=7=x=7+4=x=11
(1)小明这样写对不对?
(2)应该怎样写?× 解:x–4=7
移项,得
x=7+4
合并同类项,得
x=11练习2、解下列方程,并写出检验过程 (1)x+11=38 (2)7+x=5 (3)12x-1=11x (4)9+11x=10x-7巩固练习:本节小结本节课我们学习了什么知识?
移项的依据是什么?移项应该注意什么?作业:作业本(2)
