科学记数法[上学期]
图片预览





文档简介
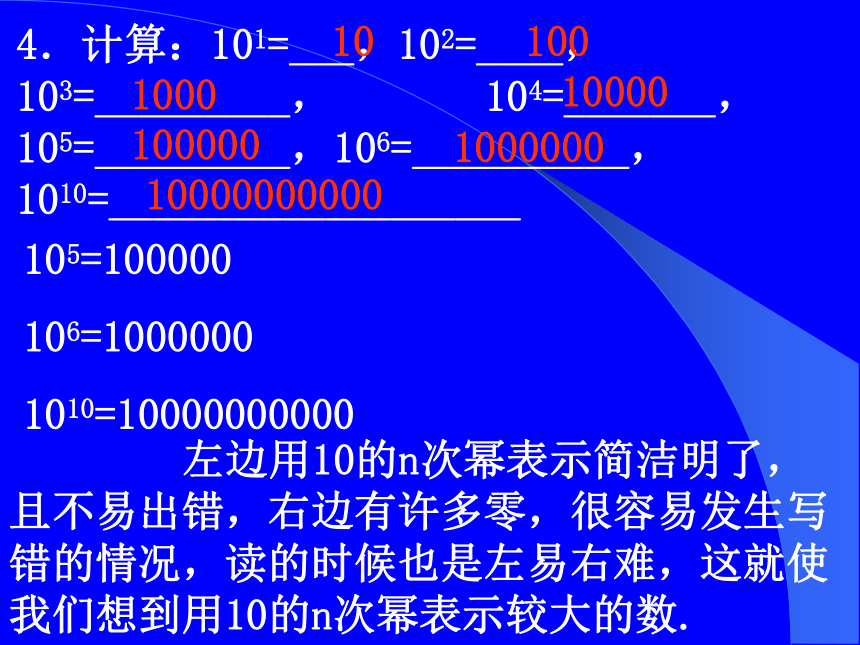
课件14张PPT。科 学 记 数 法4.计算:101=___,102=____,103=_________, 104=_______,105=_________,106=__________,1010=___________________ 10100100010000100000100000010000000000105=100000
106=1000000
1010=10000000000 左边用10的n次幂表示简洁明了,且不易出错,右边有许多零,很容易发生写错的情况,读的时候也是左易右难,这就使我们想到用10的n次幂表示较大的数. 较大的数,比如一亿,一百亿等等,像太阳的半径大约是696 000千米,光速大约是300 000 000米/秒,中国人口大约 13亿等等,能简单明了地表示它们吗?这就是本节课我们要学习的内容——科学记数法.研究10n的特征
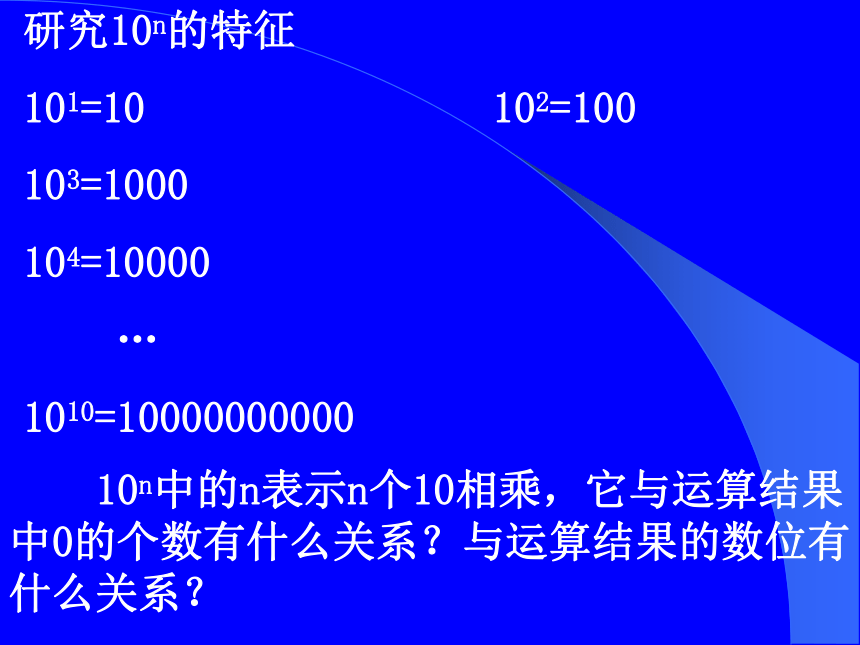
101=10 102=100
103=1000
104=10000
…
1010=10000000000 10n中的n表示n个10相乘,它与运算结果中0的个数有什么关系?与运算结果的数位有什么关系? 反之,1后面有多少个0,10的幂指数就是多少.练习(1)把下面各数写成10的幂的形式.
1000, 100000000,100000000000.1031081011练习(2)指出下列各数是几位数.
103,105,1012,10100.4613101科学记数法(1)任何一个数都可以表示成整数数位是一位数的数乘以10的n次幂的形式.如:
100=1×100=1×102
6000=6×1000=6×103
7500=7.5×1000=7.5×103 第一个等号是小学里学过的关于小数点移动的知识,我们现在把100,1000,变成10的n次幂的形式.科学记数法定义
根据上面例子,我们把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是自然数,这种记数法叫做科学记数法.用字母N表示数,
则N=a×10n(1≤|a|<10,n是整数),
这就是科学记数法.例 ?用科学记数法表示下列各数:
(1)1 000 000? (2) 57 000 000? (3) 696 000 (4) 300 000 000 (5)-78 000
(6) 12 000 000 000解:(1) 1000 000=106
(2) 57 000 000=5.7×10 000 000=5.7×107
(3) 696 000=6.96×100 000=6.96×105
(4) 300 000 000=3×100 000 000=3×108(5)-78 000= -7.8×10 000=-7.8×104
(6)12 000 000 000 =1.2×10 000 000000 =1.2×1010 如果每次都按解的步骤去做就显得有点繁, 那么利用n与数位的关系去做, 试一试:(1) 1 000 000是7位数,所以 n=6,即106
(2)57 000 000是8位数,n=7
所以57 000 000=5.7×107
(3) 696 000是6位数,n=5
所以 696 000=6.96×105
(4) 300 000 000是9位数,n=8
所以 300 000 000=3×108规律是什么?10的指数比原数的整数位数少1.1、在69600000000的以下各表示方法中,是科学记数法的为( )
(A)696× (B)69.6×
(C)6.96 × (D)0.696×
2、用科学记数法表示的数3.61× ,它的原数是( )
(A)361 00 000 000 (B)361 0 000 000
(C)361 000 000 (D)361 00 0003、在以下的各数中,最大的数为( )
(A)7.2 × (B)2.5×
(C)9.9 × (D)1× 4、在下列各数中最小的为( )
(A)3.14 × (B)3.1×
(C)3.2× (D)3.142× 5、请用科学记数法表示下列各数。
(1)我国国土面积为9597000平方千米;
(2)我国现有人口1300 000 000人;
(3)地球的表面积约为510 000 000平方千米。6、下列各数:9.99× , 1.01× , 9.9× 1.1 × 。
从小到大排列,用“ < ” 连接起来。
106=1000000
1010=10000000000 左边用10的n次幂表示简洁明了,且不易出错,右边有许多零,很容易发生写错的情况,读的时候也是左易右难,这就使我们想到用10的n次幂表示较大的数. 较大的数,比如一亿,一百亿等等,像太阳的半径大约是696 000千米,光速大约是300 000 000米/秒,中国人口大约 13亿等等,能简单明了地表示它们吗?这就是本节课我们要学习的内容——科学记数法.研究10n的特征
101=10 102=100
103=1000
104=10000
…
1010=10000000000 10n中的n表示n个10相乘,它与运算结果中0的个数有什么关系?与运算结果的数位有什么关系? 反之,1后面有多少个0,10的幂指数就是多少.练习(1)把下面各数写成10的幂的形式.
1000, 100000000,100000000000.1031081011练习(2)指出下列各数是几位数.
103,105,1012,10100.4613101科学记数法(1)任何一个数都可以表示成整数数位是一位数的数乘以10的n次幂的形式.如:
100=1×100=1×102
6000=6×1000=6×103
7500=7.5×1000=7.5×103 第一个等号是小学里学过的关于小数点移动的知识,我们现在把100,1000,变成10的n次幂的形式.科学记数法定义
根据上面例子,我们把大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是自然数,这种记数法叫做科学记数法.用字母N表示数,
则N=a×10n(1≤|a|<10,n是整数),
这就是科学记数法.例 ?用科学记数法表示下列各数:
(1)1 000 000? (2) 57 000 000? (3) 696 000 (4) 300 000 000 (5)-78 000
(6) 12 000 000 000解:(1) 1000 000=106
(2) 57 000 000=5.7×10 000 000=5.7×107
(3) 696 000=6.96×100 000=6.96×105
(4) 300 000 000=3×100 000 000=3×108(5)-78 000= -7.8×10 000=-7.8×104
(6)12 000 000 000 =1.2×10 000 000000 =1.2×1010 如果每次都按解的步骤去做就显得有点繁, 那么利用n与数位的关系去做, 试一试:(1) 1 000 000是7位数,所以 n=6,即106
(2)57 000 000是8位数,n=7
所以57 000 000=5.7×107
(3) 696 000是6位数,n=5
所以 696 000=6.96×105
(4) 300 000 000是9位数,n=8
所以 300 000 000=3×108规律是什么?10的指数比原数的整数位数少1.1、在69600000000的以下各表示方法中,是科学记数法的为( )
(A)696× (B)69.6×
(C)6.96 × (D)0.696×
2、用科学记数法表示的数3.61× ,它的原数是( )
(A)361 00 000 000 (B)361 0 000 000
(C)361 000 000 (D)361 00 0003、在以下的各数中,最大的数为( )
(A)7.2 × (B)2.5×
(C)9.9 × (D)1× 4、在下列各数中最小的为( )
(A)3.14 × (B)3.1×
(C)3.2× (D)3.142× 5、请用科学记数法表示下列各数。
(1)我国国土面积为9597000平方千米;
(2)我国现有人口1300 000 000人;
(3)地球的表面积约为510 000 000平方千米。6、下列各数:9.99× , 1.01× , 9.9× 1.1 × 。
从小到大排列,用“ < ” 连接起来。
