人教版高中数学选择性必修第一册2.1.2两条直线平行和垂直的判定 课件(共26张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册2.1.2两条直线平行和垂直的判定 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 781.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-22 21:14:37 | ||
图片预览







文档简介
(共26张PPT)
2.1.2 两条直线平行和垂直的判定
[学习目标] 1.理解并掌握两条直线平行与垂直的判定方法. 2.能根据斜率判定两直线的平行或垂直.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 是否总有l1∥l2 k1=k2
问题2 是否总有l1⊥l2 k1k2=-1
问题3 解决直线平行或垂直问题时,需注意什么?
[预习自测]
1.过点A(2,5)和点B(-4,5)的直线与直线y=3的位置关系是( )
A.相交 B.平行
C.重合 D.以上都不对
解析:由题意得过点A(2,5)和点B(-4,5)的直线为y=5,与直线y=3的斜率都为0且不重合,所以平行.
B
2.直线l1,l2的斜率是方程x2-3x-1=0的两根,则l1与l2的位置关系是
( )
A.平行 B.重合
C.相交但不垂直 D.垂直
解析:设直线l1,l2的斜率分别为k1,k2,
∵直线l1,l2的斜率是方程x2-3x-1=0的两根,
∴k1k2=-1.∴l1⊥l2.
D
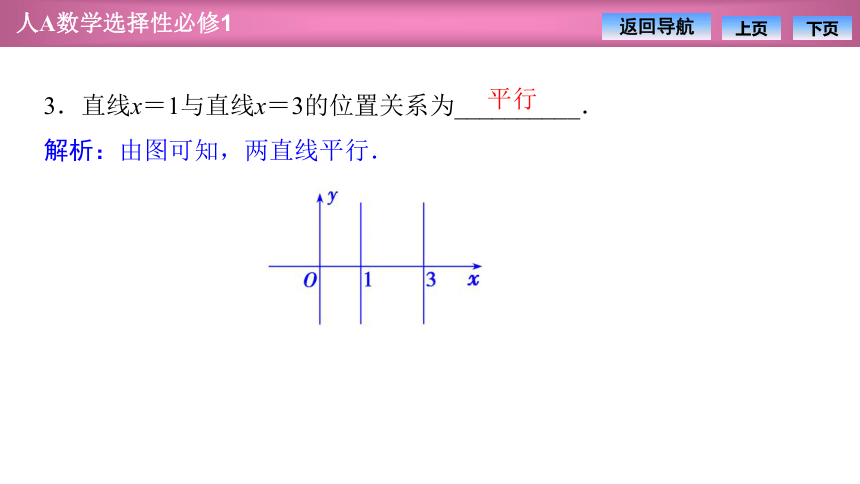
3.直线x=1与直线x=3的位置关系为__________.
解析:由图可知,两直线平行.
平行
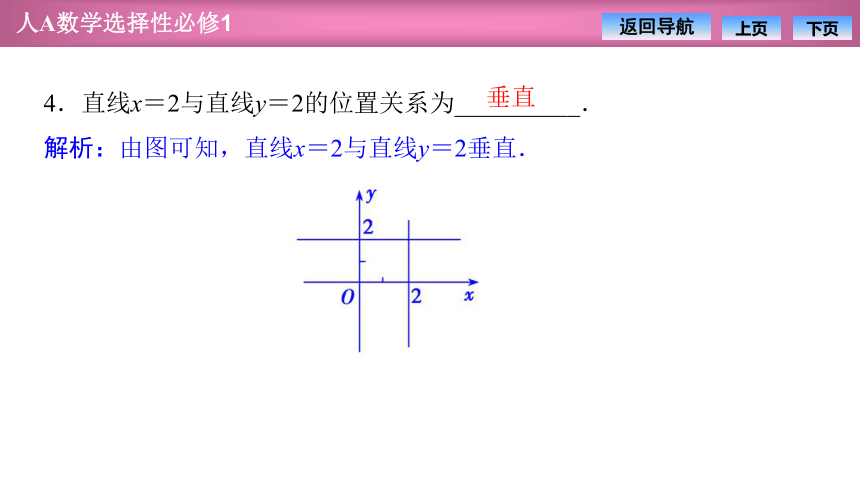
4.直线x=2与直线y=2的位置关系为__________.
解析:由图可知,直线x=2与直线y=2垂直.
垂直
直线的平行(两条直线平行)
如图,若l1∥l2,则l1与l2的倾斜角α1与α2相等,由α1=α2,可得tan α1=tan α2,即k1=k2.因此,若l1∥l2,则 .
k1=k2
反之,当k1=k2时,tan α1=tan α2,由倾斜角的取值范围及正切函数的单调性可知,α1=α2,因此 .
于是,对于斜率分别为k1,k2的两条直线l1,l2,有l1∥l2 .(若没有特殊说明,“两条直线l1,l2”指两条不重合的直线)
l1∥l2
k1=k2
判断两条直线是否平行的步骤是先判断两条直线的斜率是否都存在,即先看两点的横坐标是否相等,横坐标相等是特殊情况,应特殊判断;若都存在,再判断两条直线的斜率是否相等;若相等,还需要利用数形结合的方法判断两直线是否重合.
(1)l1∥l2 k1=k2成立的前提:两条直线l1,l2的斜率均存在.
(2)当直线的斜率都不存在且不重合时,直线l1,l2的倾斜角都是90°,则l1∥l2.
(3)当l1∥l2时,它们的斜率可能都存在且相等,也有可能斜率都不存在,但它们的倾斜角总是相等的.
1.已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
∵kAB=kCD,kBC=kDA,
∴AB∥CD,BC∥DA.
∴四边形ABCD是平行四边形.
直线的垂直(两条直线垂直)
如果两条直线都有斜率,且它们相互垂直,那么它们的斜率之积等于-1;反之,如果两条直线的斜率之积等于-1,那么它们互相垂直.即l1⊥l2 .
k1k2=-1
[例2] 判断下列各小题中的直线l1与l2是否垂直.
(1)l1经过点A(-1,-2),B(1,2),l2经过点M(-2,-1),N(2,1);
(2)l1的斜率为-10,l2经过点A(10,2),B(20,3);
(3)l1经过点A(3,4),B(3,100),l2经过点M(-10,40),N(10,40).
分析:知道直线经过的两点,计算直线的斜率,由斜率之间的关系判断直线的位置关系,若两条直线中的一条没有斜率,另一条斜率为零,则两条直线互相垂直.
判断直线之间的位置关系,首先看直线的斜率,若直线经过的两点中横坐标相等,则直线无斜率;若两点的纵坐标相等,则直线的斜率为零.
两条直线垂直与斜率之间的关系:
2.已知△ABC三个顶点坐标分别为A(-2,-4),B(6,6),C(0,6),求此三角形三边的高所在直线的斜率.
1.知识清单:(1)两条直线平行.
(2)两条直线垂直.
2.方法归纳:数形结合、分类讨论.
3.常见误区:讨论两条直线位置关系时,忽略直线斜率不存在的情况.
课时作业 巩固提升
2.1.2 两条直线平行和垂直的判定
[学习目标] 1.理解并掌握两条直线平行与垂直的判定方法. 2.能根据斜率判定两直线的平行或垂直.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 是否总有l1∥l2 k1=k2
问题2 是否总有l1⊥l2 k1k2=-1
问题3 解决直线平行或垂直问题时,需注意什么?
[预习自测]
1.过点A(2,5)和点B(-4,5)的直线与直线y=3的位置关系是( )
A.相交 B.平行
C.重合 D.以上都不对
解析:由题意得过点A(2,5)和点B(-4,5)的直线为y=5,与直线y=3的斜率都为0且不重合,所以平行.
B
2.直线l1,l2的斜率是方程x2-3x-1=0的两根,则l1与l2的位置关系是
( )
A.平行 B.重合
C.相交但不垂直 D.垂直
解析:设直线l1,l2的斜率分别为k1,k2,
∵直线l1,l2的斜率是方程x2-3x-1=0的两根,
∴k1k2=-1.∴l1⊥l2.
D
3.直线x=1与直线x=3的位置关系为__________.
解析:由图可知,两直线平行.
平行
4.直线x=2与直线y=2的位置关系为__________.
解析:由图可知,直线x=2与直线y=2垂直.
垂直
直线的平行(两条直线平行)
如图,若l1∥l2,则l1与l2的倾斜角α1与α2相等,由α1=α2,可得tan α1=tan α2,即k1=k2.因此,若l1∥l2,则 .
k1=k2
反之,当k1=k2时,tan α1=tan α2,由倾斜角的取值范围及正切函数的单调性可知,α1=α2,因此 .
于是,对于斜率分别为k1,k2的两条直线l1,l2,有l1∥l2 .(若没有特殊说明,“两条直线l1,l2”指两条不重合的直线)
l1∥l2
k1=k2
判断两条直线是否平行的步骤是先判断两条直线的斜率是否都存在,即先看两点的横坐标是否相等,横坐标相等是特殊情况,应特殊判断;若都存在,再判断两条直线的斜率是否相等;若相等,还需要利用数形结合的方法判断两直线是否重合.
(1)l1∥l2 k1=k2成立的前提:两条直线l1,l2的斜率均存在.
(2)当直线的斜率都不存在且不重合时,直线l1,l2的倾斜角都是90°,则l1∥l2.
(3)当l1∥l2时,它们的斜率可能都存在且相等,也有可能斜率都不存在,但它们的倾斜角总是相等的.
1.已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
∵kAB=kCD,kBC=kDA,
∴AB∥CD,BC∥DA.
∴四边形ABCD是平行四边形.
直线的垂直(两条直线垂直)
如果两条直线都有斜率,且它们相互垂直,那么它们的斜率之积等于-1;反之,如果两条直线的斜率之积等于-1,那么它们互相垂直.即l1⊥l2 .
k1k2=-1
[例2] 判断下列各小题中的直线l1与l2是否垂直.
(1)l1经过点A(-1,-2),B(1,2),l2经过点M(-2,-1),N(2,1);
(2)l1的斜率为-10,l2经过点A(10,2),B(20,3);
(3)l1经过点A(3,4),B(3,100),l2经过点M(-10,40),N(10,40).
分析:知道直线经过的两点,计算直线的斜率,由斜率之间的关系判断直线的位置关系,若两条直线中的一条没有斜率,另一条斜率为零,则两条直线互相垂直.
判断直线之间的位置关系,首先看直线的斜率,若直线经过的两点中横坐标相等,则直线无斜率;若两点的纵坐标相等,则直线的斜率为零.
两条直线垂直与斜率之间的关系:
2.已知△ABC三个顶点坐标分别为A(-2,-4),B(6,6),C(0,6),求此三角形三边的高所在直线的斜率.
1.知识清单:(1)两条直线平行.
(2)两条直线垂直.
2.方法归纳:数形结合、分类讨论.
3.常见误区:讨论两条直线位置关系时,忽略直线斜率不存在的情况.
课时作业 巩固提升
