2023-2024学年北师大版数学九年级上册第六章反比例函数单元同步测试卷(含解析版)
文档属性
| 名称 | 2023-2024学年北师大版数学九年级上册第六章反比例函数单元同步测试卷(含解析版) | 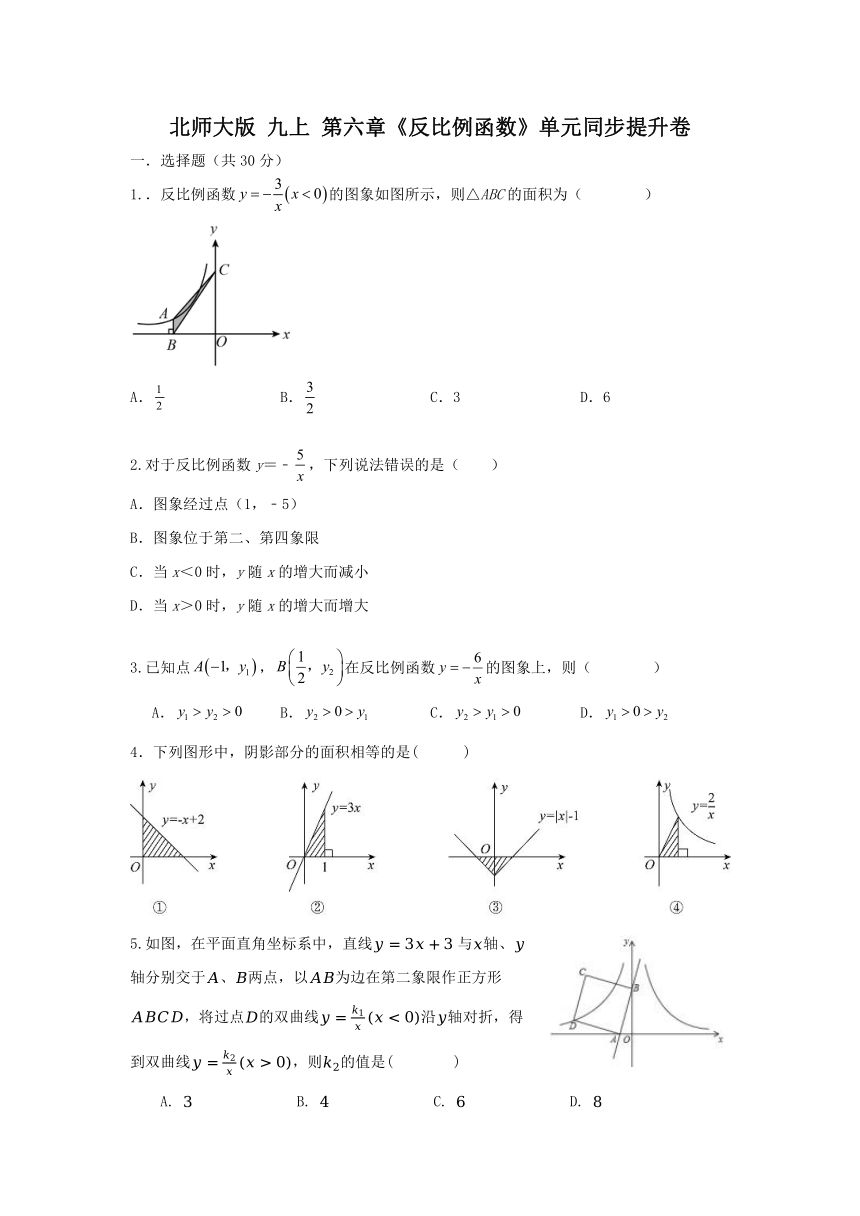 | |
| 格式 | docx | ||
| 文件大小 | 813.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 18:05:11 | ||
图片预览




文档简介
北师大版 九上 第六章《反比例函数》单元同步提升卷
选择题(共30分)
1..反比例函数的图象如图所示,则△ABC的面积为( )
A. B. C.3 D.6
2.对于反比例函数y=﹣,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
3.已知点,在反比例函数的图象上,则( )
B. C. D.
4.下列图形中,阴影部分的面积相等的是( )
5.如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第二象限作正方形,将过点的双曲线沿轴对折,得到双曲线,则的值是( )
B. C. D.
6.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
7。某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
甲 B.乙 C.丙 D.丁
8.如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
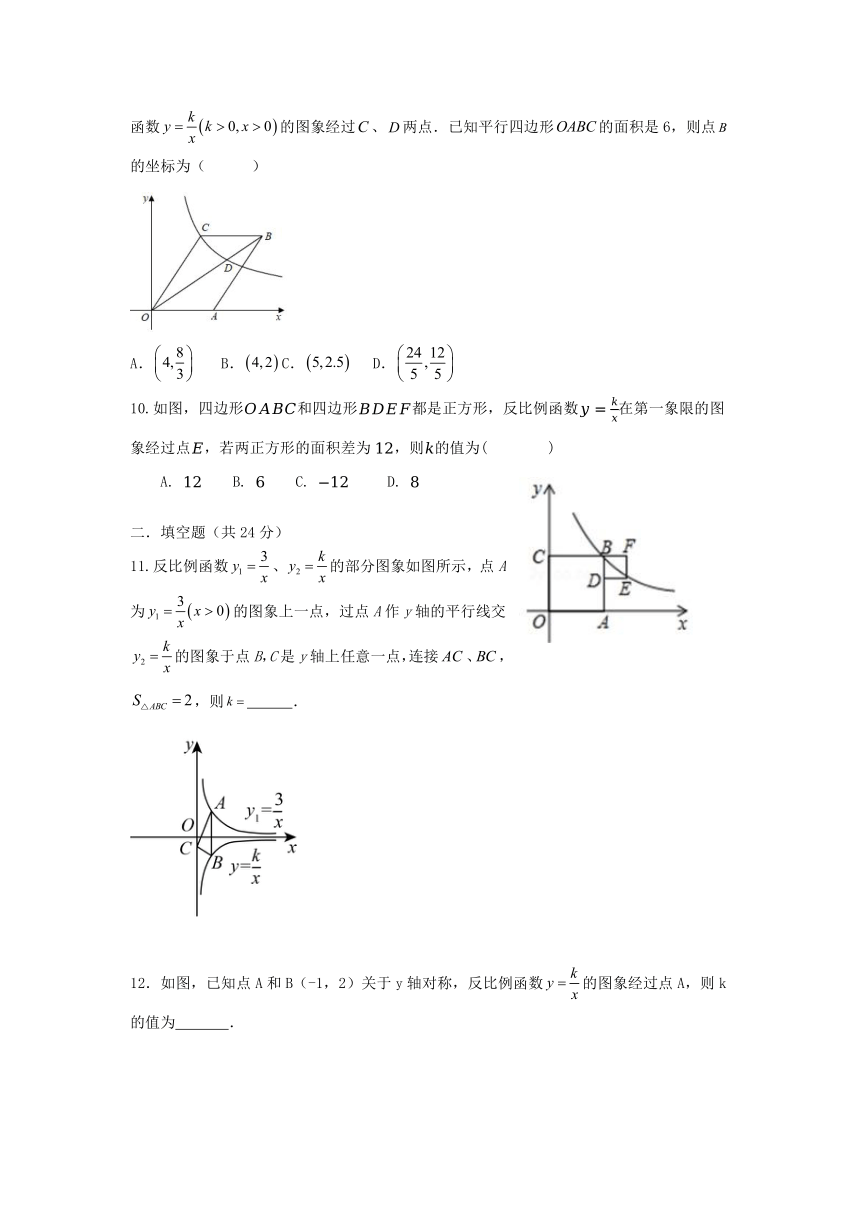
9.如图,平行四边形的项点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是6,则点的坐标为( )
A. B. C. D.
10.如图,四边形和四边形都是正方形,反比例函数在第一象限的图象经过点,若两正方形的面积差为,则的值为( )
A. B. C. D.
填空题(共24分)
11.反比例函数、的部分图象如图所示,点A为的图象上一点,过点A作y轴的平行线交的图象于点B,C是y轴上任意一点,连接、,,则 .
12.如图,已知点A和B(-1,2)关于y轴对称,反比例函数的图象经过点A,则k的值为 .
13.如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图像经过点C,E.若点,则k的值是_________.
14.已知:点在直线上,也在双曲线上,则的值为______。
15.如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是_____.
16.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数y=的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EFCD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于,其中正确的有___________(填序号)
解答题(共66分)
17.(6分)已知反比例函数的图像过点.
(1)若在这一个函数的每一个分支上,随增大而减少,求的取值范围;
(2)若一次函数的图像与反比例函数的图像只有一个交点,求一次函数的表达式.
18.(8分)(6分)如图,已知直线y=-x上一点B,由点B分别向x轴、y轴作垂线,垂足为A、C,若A点的坐标为(0,5).
(1)若点B也在一反比例函数的图象上,求出此反比例函数的表达式.
(2)若将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,求点E的坐标.
19.(8分)如图,在平面直角坐标系中,B、C两点在x轴的正半轴上,以线段BC为边向上作正方形ABCD,顶点A在正比例函数y=2x的图象上,反比例函数y=(x>0,k>0)的图象经过点A,且与边CD相交于点E.
(1)若BC=4,求点E的坐标;
(2)连接AE,OE,若△AOE的面积为16,求k的值.
20.(10分)如图,点是反比例函数与一次函数在轴上方的图象的交点,过点作轴,垂足是点,.一次函数的图象与轴的正半轴交于点.
(1)求点的坐标;
(2)若梯形的面积是3,求一次函数的解析式;
(3)结合这两个函数的完整图象:当时,写出的取值范围
.
21.(10分)如图,一次函数与反比例函数的图象交于,两点,与坐标轴分别交于,两点.
求一次函数的表达式
根据图象直接写出中的取值范围
求的面积.
22.(12分)如图,四边形OBAC是矩形,OC=2,OB=6,反比例函数的图象过点A.
(1)求k的值.
(2)点P为反比例函数图象上的一点,作PD⊥直线AC,PE⊥x轴,当四边形PDCE是正方形时,求点P的坐标.
(3)点G为坐标平面上的一点,在反比例函数的图象上是否存在一点Q,使得以A、B、Q、G为顶点组成的平行四边形面积为16?若存在,请求出点G的坐标;若不存在,请说明理由.
23.(12分)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
(1)直接写出反比例函数的解析式;
(2)求一次函数的解析式;
(3)在y轴上是否存在一点P,使得△PDC与△CDO相似?若存在求P点的坐标,若不存在说明理由。
北师大版 九上 第六章《反比例函数》单元同步提升卷(答案版)
选择题(共30分)
1..反比例函数的图象如图所示,则△ABC的面积为( )
A. B. C.3 D.6
答案B
2.对于反比例函数y=﹣,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
答案 C
3.已知点,在反比例函数的图象上,则( )
B. C. D.
答案 D
【分析】将,两点坐标代入函数解析式中,直接比较结果的大小即可.
【详解】解:将代入中得:,
代入中得:,
则,
故选:D.
4.下列图形中,阴影部分的面积相等的是( )
答案 C
【详解】解:①直线y=-x+2与坐标轴的交点坐标为:(2,0),(0,2),故S阴影=×2×2=2;
②直线y=3x与x=1的交点坐标为(1,3),所以S阴影=×1×3=;
③y=与坐标轴交于:(-1,0),(1,0),(0,-1),故阴影部分的三角形是等腰直角三角形,其面积S=×2×1=1.
④此函数是反比例函数,那么阴影部分的面积为:S=×|2|=1;
故答案为C.
5.如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第二象限作正方形,将过点的双曲线沿轴对折,得到双曲线,则的值是( )
B. C. D.
【答案】
【解析】解:如图,过点作轴于点,则
在中,令,得,,
令,得,解得,,
,,
四边形是正方形,
,
在和中
≌
,
把代入中,得
;
双曲线沿轴对折,得到双曲线,
即双曲线与双曲线关于轴对称,
.
故选:.
6.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
答案D
7。某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
甲 B.乙 C.丙 D.丁
答案 C
8.如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
答案 C
9.如图,平行四边形的项点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是6,则点的坐标为( )
A. B. C. D.
解:∵点D(2,1)在反比例函数上,
∴k=2×1=2,
∴反比例函数解析式为:,
设直线OB的函数解析式为y=mx,
∵点D(2,1)在对角线OB上,
∴2m=1,即,
∴OB的解析式为:,
∵点C在反比例函数图象上,
∴设点C坐标为(a,),
∵四边形OABC为平行四边形,
∴BCOA,
∴点B的纵坐标为,
将y=代入,
解得:x=,
∴点B坐标为(,),
∴BC=,
∵平行四边形OABC的面积是6,
∴()×=6,
解得:a=1或a=-1(舍去),
∴,,
∴点B坐标为:,
故选:B.
10.如图,四边形和四边形都是正方形,反比例函数在第一象限的图象经过点,若两正方形的面积差为,则的值为( )
A. B. C. D.
【答案】
【解答】
解:设正方形、的边长分别为和,则,,
所以,
所以,
,
,
两正方形的面积差为,
.
故选:.
填空题(共24分)
11.反比例函数、的部分图象如图所示,点A为的图象上一点,过点A作y轴的平行线交的图象于点B,C是y轴上任意一点,连接、,,则 .
答案 .
【分析】连接,设与x轴交于点D,根据,得出,根据,得出,求出,根据,即可得出答案.
【详解】解:连接,设与x轴交于点D,如图所示:
∵,
∴,
∵,
∴,
解得:,
∵,
∴.
故答案为:.
12.如图,已知点A和B(-1,2)关于y轴对称,反比例函数的图象经过点A,则k的值为 .
答案 .2.
【详解】试题分析:∵点A和B(-1,2)关于y轴对称,
∴A(1,2)
13.如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图像经过点C,E.若点,则k的值是_________.
答案 4
∵反比例函数y=的图象经过点A(1,2),
∴2=,
解得k=2.
14.已知:点在直线上,也在双曲线上,则的值为______。
【答案】
解:点在直线上,
,
点在双曲线上,
,
.
故答案为:.
15.如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是_____.
解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
∴∠AEB=∠CDO=90°,
∵平行四边形OABC,
∴AE=CD,AB=CO,
∴,
在反比例函数y=中,△COD的面积=,
∴△ABE的面积=△COD的面积=,
同理得△AOE的面积=△CBD的面积=,
综上平行四边形OABC的面积为.
故答案为.
16.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数y=的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EFCD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于,其中正确的有___________(填序号)
解:设点D的坐标为(x,),则F(x,0).
由函数的图象可知:x>0,k>0.
∴,
同理可得,故⑤正确;
故△CEF与△DEF的面积相等.故①正确;
若两个三角形以EF为底,则EF边上的高相等,故CDEF.故②正确;
③条件不足,无法得到判定△DCE和△CDF全等的条件,故③错误;
④∵CDEF,CE⊥y轴、DF⊥x轴,
∴CEAF、DFBE,
∴四边形ACEF,四边形DBEF都是平行四边形,
而且EF是公共边,
即AC=EF=BD,
∴BD=AC,故④正确;
因此正确的结论有4个:①②④⑤.
故答案为:①②④⑤.
解答题(共66分)
17.(6分)已知反比例函数的图像过点.
(1)若在这一个函数的每一个分支上,随增大而减少,求的取值范围;
(2)若一次函数的图像与反比例函数的图像只有一个交点,求一次函数的表达式.
(1)解:∵在函数的每一个分支上,随增大而减少,
∴,
∴;
(2)解:∵反比例函数的图像过点,
∴,
解得,
∴,
∵一次函数的图像与反比例函数的图像只有一个交点,
18.(8分)(6分)如图,已知直线y=-x上一点B,由点B分别向x轴、y轴作垂线,垂足为A、C,若A点的坐标为(0,5).
(1)若点B也在一反比例函数的图象上,求出此反比例函数的表达式.
(2)若将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,求点E的坐标.
解:(1)由题意得点B纵坐标为5.
又∵点B在直线y=-x上,
∴ B点坐标为(-,5).
设过点 B的反比例函数的表达式为y=,
k=-×5=-,
∴此反比例函数的表达式为;
(2)设点E坐标为(a,b).
∵点E在直线y=-x上,
∴ b=-a.
∵ OE=OA=5,
∴ ,
解得或.
∵点E在第二象限,
∴ E点坐标为(-4,3).
19.(8分)如图,在平面直角坐标系中,B、C两点在x轴的正半轴上,以线段BC为边向上作正方形ABCD,顶点A在正比例函数y=2x的图象上,反比例函数y=(x>0,k>0)的图象经过点A,且与边CD相交于点E.
(1)若BC=4,求点E的坐标;
(2)连接AE,OE,若△AOE的面积为16,求k的值.
(1)解:在正方形ABCD中,AB=BC=4,
∴A(2,4),
∵A(2,4)在y=的图象上,
∴k=2×4=8,
∵OC=OB+BC=6,
∴=6,
将=6代入y=中,得:=,
∴点E的坐标为(6,).
(2)解:设A(a,2a)(a>0),则点E(3a, ),
根据反比例函数的几何意义得,
∴,
∴
得,
∴k=.
20.(10分)如图,点是反比例函数与一次函数在轴上方的图象的交点,过点作轴,垂足是点,.一次函数的图象与轴的正半轴交于点.
(1)求点的坐标;
(2)若梯形的面积是3,求一次函数的解析式;
(3)结合这两个函数的完整图象:当时,写出的取值范围
答案 【详解】解:(1)∵点在的图像上,轴,.
∴,
∴
∴点的坐标为;
(2)∵梯形的面积是3,
∴,
解得,
∴点的坐标为,
把点与代入
得
解得:,.
∴一次函数的解析式为.
(3)由题意可知,作出函数和函数图像如下图所示:
设函数和函数的另一个交点为E,
联立 ,得
点E的坐标为
即 的函数图像要在的函数图像上面,
可将图像分割成如下图所示:
由图像可知所对应的自变量的取值范围为:或.
21.(10分)如图,一次函数与反比例函数的图象交于,两点,与坐标轴分别交于,两点.
求一次函数的表达式
根据图象直接写出中的取值范围
求的面积.
解:点在反比例函数的图象上,解得.点的坐标为又点也在反比例函数的图象上,解得.点的坐标为又点,在一次函数的图象上,解得一次函数的表达式为
根据图象,得时,的取值范围为或
直线与轴的交点为,点的坐标为..
22.(12分)如图,四边形OBAC是矩形,OC=2,OB=6,反比例函数的图象过点A.
(1)求k的值.
(2)点P为反比例函数图象上的一点,作PD⊥直线AC,PE⊥x轴,当四边形PDCE是正方形时,求点P的坐标.
(3)点G为坐标平面上的一点,在反比例函数的图象上是否存在一点Q,使得以A、B、Q、G为顶点组成的平行四边形面积为16?若存在,请求出点G的坐标;若不存在,请说明理由.
解:(1)∵OC=2,OB=6,
∴点C(2,0),点B(0,6),点A(2,6),
∵反比例函数的图象过点A,
∴k=2×6=12;
(2)∵k=12,
∴反比例函数解析式为:,
设,
∵四边形PDCE是正方形,
∴PD=PE,
当点P在第一象限时,
∴,
解得(舍去)
∴
当点P在第三象限,
∴
解得:(舍去)
∴,
综上所述,或
(3)设点的坐标为
若AB为边,
∵以A、B、Q、G为顶点组成的平行四边形面积为16,
∴,
解得:或,
∴或,
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB=QG=2,AB∥QG,
∴或或或,
若AB为对角线,
设点G(x,y),
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB与QG互相平分,
∵以A、B、Q、G为顶点组成的平行四边形面积为16,
或,
∴或
解得或
23.(12分)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
(1)直接写出反比例函数的解析式;
(2)求一次函数的解析式;
(3)在y轴上是否存在一点P,使得△PDC与△CDO相似?若存在求P点的坐标,若不存在说明理由.
(1)解:把A(1,3)代入反比例解析式得:3=,即k=3,
则反比例解析式为y=;
(2)解:∵B(m,-2)在反比例函数y=上,
∴-2=,即m=-,即B(-,-2),
把A与B坐标代入一次函数解析式得:,
解得:,
则一次函数解析式为y=x-1;
(3)解:若P与O重合,显然成立;
若P与O不重合,在y轴上存在一点P,使得△PDC与△CDO相似,理由为:过点C作CP⊥AB,交y轴于点P,如图所示,
∵C、D两点在直线y=x-1上,
∴C、D的坐标分别为C(,0),D(0,-1),
∴OC=,OD=1,DC=,
∵△PDC∽△CDO,
∴=,即=,
解得:PD=,
∴OP=DP-OD=-1=,
则点P的坐标为(0,).
综上所示,P的坐标为(0,0)或(0,)
选择题(共30分)
1..反比例函数的图象如图所示,则△ABC的面积为( )
A. B. C.3 D.6
2.对于反比例函数y=﹣,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
3.已知点,在反比例函数的图象上,则( )
B. C. D.
4.下列图形中,阴影部分的面积相等的是( )
5.如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第二象限作正方形,将过点的双曲线沿轴对折,得到双曲线,则的值是( )
B. C. D.
6.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
7。某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
甲 B.乙 C.丙 D.丁
8.如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
9.如图,平行四边形的项点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是6,则点的坐标为( )
A. B. C. D.
10.如图,四边形和四边形都是正方形,反比例函数在第一象限的图象经过点,若两正方形的面积差为,则的值为( )
A. B. C. D.
填空题(共24分)
11.反比例函数、的部分图象如图所示,点A为的图象上一点,过点A作y轴的平行线交的图象于点B,C是y轴上任意一点,连接、,,则 .
12.如图,已知点A和B(-1,2)关于y轴对称,反比例函数的图象经过点A,则k的值为 .
13.如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图像经过点C,E.若点,则k的值是_________.
14.已知:点在直线上,也在双曲线上,则的值为______。
15.如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是_____.
16.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数y=的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EFCD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于,其中正确的有___________(填序号)
解答题(共66分)
17.(6分)已知反比例函数的图像过点.
(1)若在这一个函数的每一个分支上,随增大而减少,求的取值范围;
(2)若一次函数的图像与反比例函数的图像只有一个交点,求一次函数的表达式.
18.(8分)(6分)如图,已知直线y=-x上一点B,由点B分别向x轴、y轴作垂线,垂足为A、C,若A点的坐标为(0,5).
(1)若点B也在一反比例函数的图象上,求出此反比例函数的表达式.
(2)若将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,求点E的坐标.
19.(8分)如图,在平面直角坐标系中,B、C两点在x轴的正半轴上,以线段BC为边向上作正方形ABCD,顶点A在正比例函数y=2x的图象上,反比例函数y=(x>0,k>0)的图象经过点A,且与边CD相交于点E.
(1)若BC=4,求点E的坐标;
(2)连接AE,OE,若△AOE的面积为16,求k的值.
20.(10分)如图,点是反比例函数与一次函数在轴上方的图象的交点,过点作轴,垂足是点,.一次函数的图象与轴的正半轴交于点.
(1)求点的坐标;
(2)若梯形的面积是3,求一次函数的解析式;
(3)结合这两个函数的完整图象:当时,写出的取值范围
.
21.(10分)如图,一次函数与反比例函数的图象交于,两点,与坐标轴分别交于,两点.
求一次函数的表达式
根据图象直接写出中的取值范围
求的面积.
22.(12分)如图,四边形OBAC是矩形,OC=2,OB=6,反比例函数的图象过点A.
(1)求k的值.
(2)点P为反比例函数图象上的一点,作PD⊥直线AC,PE⊥x轴,当四边形PDCE是正方形时,求点P的坐标.
(3)点G为坐标平面上的一点,在反比例函数的图象上是否存在一点Q,使得以A、B、Q、G为顶点组成的平行四边形面积为16?若存在,请求出点G的坐标;若不存在,请说明理由.
23.(12分)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
(1)直接写出反比例函数的解析式;
(2)求一次函数的解析式;
(3)在y轴上是否存在一点P,使得△PDC与△CDO相似?若存在求P点的坐标,若不存在说明理由。
北师大版 九上 第六章《反比例函数》单元同步提升卷(答案版)
选择题(共30分)
1..反比例函数的图象如图所示,则△ABC的面积为( )
A. B. C.3 D.6
答案B
2.对于反比例函数y=﹣,下列说法错误的是( )
A.图象经过点(1,﹣5)
B.图象位于第二、第四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
答案 C
3.已知点,在反比例函数的图象上,则( )
B. C. D.
答案 D
【分析】将,两点坐标代入函数解析式中,直接比较结果的大小即可.
【详解】解:将代入中得:,
代入中得:,
则,
故选:D.
4.下列图形中,阴影部分的面积相等的是( )
答案 C
【详解】解:①直线y=-x+2与坐标轴的交点坐标为:(2,0),(0,2),故S阴影=×2×2=2;
②直线y=3x与x=1的交点坐标为(1,3),所以S阴影=×1×3=;
③y=与坐标轴交于:(-1,0),(1,0),(0,-1),故阴影部分的三角形是等腰直角三角形,其面积S=×2×1=1.
④此函数是反比例函数,那么阴影部分的面积为:S=×|2|=1;
故答案为C.
5.如图,在平面直角坐标系中,直线与轴、轴分别交于、两点,以为边在第二象限作正方形,将过点的双曲线沿轴对折,得到双曲线,则的值是( )
B. C. D.
【答案】
【解析】解:如图,过点作轴于点,则
在中,令,得,,
令,得,解得,,
,,
四边形是正方形,
,
在和中
≌
,
把代入中,得
;
双曲线沿轴对折,得到双曲线,
即双曲线与双曲线关于轴对称,
.
故选:.
6.如图,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且直线l分别与反比例函数和的图象交于P、Q两点.若S△POQ=15,则k的值为( )
A.38 B.22 C.﹣7 D.﹣22
答案D
7。某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
甲 B.乙 C.丙 D.丁
答案 C
8.如图,在平面直角坐标系中,直线y=x与反比例函数y=(x>0)的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交y轴于点B,交反比例函数图象于点C.若OA=2BC,则b的值为( )
A.1 B.2 C.3 D.4
答案 C
9.如图,平行四边形的项点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是6,则点的坐标为( )
A. B. C. D.
解:∵点D(2,1)在反比例函数上,
∴k=2×1=2,
∴反比例函数解析式为:,
设直线OB的函数解析式为y=mx,
∵点D(2,1)在对角线OB上,
∴2m=1,即,
∴OB的解析式为:,
∵点C在反比例函数图象上,
∴设点C坐标为(a,),
∵四边形OABC为平行四边形,
∴BCOA,
∴点B的纵坐标为,
将y=代入,
解得:x=,
∴点B坐标为(,),
∴BC=,
∵平行四边形OABC的面积是6,
∴()×=6,
解得:a=1或a=-1(舍去),
∴,,
∴点B坐标为:,
故选:B.
10.如图,四边形和四边形都是正方形,反比例函数在第一象限的图象经过点,若两正方形的面积差为,则的值为( )
A. B. C. D.
【答案】
【解答】
解:设正方形、的边长分别为和,则,,
所以,
所以,
,
,
两正方形的面积差为,
.
故选:.
填空题(共24分)
11.反比例函数、的部分图象如图所示,点A为的图象上一点,过点A作y轴的平行线交的图象于点B,C是y轴上任意一点,连接、,,则 .
答案 .
【分析】连接,设与x轴交于点D,根据,得出,根据,得出,求出,根据,即可得出答案.
【详解】解:连接,设与x轴交于点D,如图所示:
∵,
∴,
∵,
∴,
解得:,
∵,
∴.
故答案为:.
12.如图,已知点A和B(-1,2)关于y轴对称,反比例函数的图象经过点A,则k的值为 .
答案 .2.
【详解】试题分析:∵点A和B(-1,2)关于y轴对称,
∴A(1,2)
13.如图,在平面直角坐标系中,正方形的顶点A,B分别在x轴、y轴上,对角线交于点E,反比例函数的图像经过点C,E.若点,则k的值是_________.
答案 4
∵反比例函数y=的图象经过点A(1,2),
∴2=,
解得k=2.
14.已知:点在直线上,也在双曲线上,则的值为______。
【答案】
解:点在直线上,
,
点在双曲线上,
,
.
故答案为:.
15.如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=(k1<0)上,顶点C在y=(k2>0)上,则平行四边形OABC的面积是_____.
解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
∴∠AEB=∠CDO=90°,
∵平行四边形OABC,
∴AE=CD,AB=CO,
∴,
在反比例函数y=中,△COD的面积=,
∴△ABE的面积=△COD的面积=,
同理得△AOE的面积=△CBD的面积=,
综上平行四边形OABC的面积为.
故答案为.
16.如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数y=的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EFCD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于,其中正确的有___________(填序号)
解:设点D的坐标为(x,),则F(x,0).
由函数的图象可知:x>0,k>0.
∴,
同理可得,故⑤正确;
故△CEF与△DEF的面积相等.故①正确;
若两个三角形以EF为底,则EF边上的高相等,故CDEF.故②正确;
③条件不足,无法得到判定△DCE和△CDF全等的条件,故③错误;
④∵CDEF,CE⊥y轴、DF⊥x轴,
∴CEAF、DFBE,
∴四边形ACEF,四边形DBEF都是平行四边形,
而且EF是公共边,
即AC=EF=BD,
∴BD=AC,故④正确;
因此正确的结论有4个:①②④⑤.
故答案为:①②④⑤.
解答题(共66分)
17.(6分)已知反比例函数的图像过点.
(1)若在这一个函数的每一个分支上,随增大而减少,求的取值范围;
(2)若一次函数的图像与反比例函数的图像只有一个交点,求一次函数的表达式.
(1)解:∵在函数的每一个分支上,随增大而减少,
∴,
∴;
(2)解:∵反比例函数的图像过点,
∴,
解得,
∴,
∵一次函数的图像与反比例函数的图像只有一个交点,
18.(8分)(6分)如图,已知直线y=-x上一点B,由点B分别向x轴、y轴作垂线,垂足为A、C,若A点的坐标为(0,5).
(1)若点B也在一反比例函数的图象上,求出此反比例函数的表达式.
(2)若将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,求点E的坐标.
解:(1)由题意得点B纵坐标为5.
又∵点B在直线y=-x上,
∴ B点坐标为(-,5).
设过点 B的反比例函数的表达式为y=,
k=-×5=-,
∴此反比例函数的表达式为;
(2)设点E坐标为(a,b).
∵点E在直线y=-x上,
∴ b=-a.
∵ OE=OA=5,
∴ ,
解得或.
∵点E在第二象限,
∴ E点坐标为(-4,3).
19.(8分)如图,在平面直角坐标系中,B、C两点在x轴的正半轴上,以线段BC为边向上作正方形ABCD,顶点A在正比例函数y=2x的图象上,反比例函数y=(x>0,k>0)的图象经过点A,且与边CD相交于点E.
(1)若BC=4,求点E的坐标;
(2)连接AE,OE,若△AOE的面积为16,求k的值.
(1)解:在正方形ABCD中,AB=BC=4,
∴A(2,4),
∵A(2,4)在y=的图象上,
∴k=2×4=8,
∵OC=OB+BC=6,
∴=6,
将=6代入y=中,得:=,
∴点E的坐标为(6,).
(2)解:设A(a,2a)(a>0),则点E(3a, ),
根据反比例函数的几何意义得,
∴,
∴
得,
∴k=.
20.(10分)如图,点是反比例函数与一次函数在轴上方的图象的交点,过点作轴,垂足是点,.一次函数的图象与轴的正半轴交于点.
(1)求点的坐标;
(2)若梯形的面积是3,求一次函数的解析式;
(3)结合这两个函数的完整图象:当时,写出的取值范围
答案 【详解】解:(1)∵点在的图像上,轴,.
∴,
∴
∴点的坐标为;
(2)∵梯形的面积是3,
∴,
解得,
∴点的坐标为,
把点与代入
得
解得:,.
∴一次函数的解析式为.
(3)由题意可知,作出函数和函数图像如下图所示:
设函数和函数的另一个交点为E,
联立 ,得
点E的坐标为
即 的函数图像要在的函数图像上面,
可将图像分割成如下图所示:
由图像可知所对应的自变量的取值范围为:或.
21.(10分)如图,一次函数与反比例函数的图象交于,两点,与坐标轴分别交于,两点.
求一次函数的表达式
根据图象直接写出中的取值范围
求的面积.
解:点在反比例函数的图象上,解得.点的坐标为又点也在反比例函数的图象上,解得.点的坐标为又点,在一次函数的图象上,解得一次函数的表达式为
根据图象,得时,的取值范围为或
直线与轴的交点为,点的坐标为..
22.(12分)如图,四边形OBAC是矩形,OC=2,OB=6,反比例函数的图象过点A.
(1)求k的值.
(2)点P为反比例函数图象上的一点,作PD⊥直线AC,PE⊥x轴,当四边形PDCE是正方形时,求点P的坐标.
(3)点G为坐标平面上的一点,在反比例函数的图象上是否存在一点Q,使得以A、B、Q、G为顶点组成的平行四边形面积为16?若存在,请求出点G的坐标;若不存在,请说明理由.
解:(1)∵OC=2,OB=6,
∴点C(2,0),点B(0,6),点A(2,6),
∵反比例函数的图象过点A,
∴k=2×6=12;
(2)∵k=12,
∴反比例函数解析式为:,
设,
∵四边形PDCE是正方形,
∴PD=PE,
当点P在第一象限时,
∴,
解得(舍去)
∴
当点P在第三象限,
∴
解得:(舍去)
∴,
综上所述,或
(3)设点的坐标为
若AB为边,
∵以A、B、Q、G为顶点组成的平行四边形面积为16,
∴,
解得:或,
∴或,
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB=QG=2,AB∥QG,
∴或或或,
若AB为对角线,
设点G(x,y),
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB与QG互相平分,
∵以A、B、Q、G为顶点组成的平行四边形面积为16,
或,
∴或
解得或
23.(12分)如图,一次函数y=ax+b的图象与反比例函数y=的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知A(3,1),点B的坐标为(m,-2).
(1)直接写出反比例函数的解析式;
(2)求一次函数的解析式;
(3)在y轴上是否存在一点P,使得△PDC与△CDO相似?若存在求P点的坐标,若不存在说明理由.
(1)解:把A(1,3)代入反比例解析式得:3=,即k=3,
则反比例解析式为y=;
(2)解:∵B(m,-2)在反比例函数y=上,
∴-2=,即m=-,即B(-,-2),
把A与B坐标代入一次函数解析式得:,
解得:,
则一次函数解析式为y=x-1;
(3)解:若P与O重合,显然成立;
若P与O不重合,在y轴上存在一点P,使得△PDC与△CDO相似,理由为:过点C作CP⊥AB,交y轴于点P,如图所示,
∵C、D两点在直线y=x-1上,
∴C、D的坐标分别为C(,0),D(0,-1),
∴OC=,OD=1,DC=,
∵△PDC∽△CDO,
∴=,即=,
解得:PD=,
∴OP=DP-OD=-1=,
则点P的坐标为(0,).
综上所示,P的坐标为(0,0)或(0,)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
