1.2.3 相 反 数[上学期]
文档属性
| 名称 | 1.2.3 相 反 数[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 289.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-07 22:51:00 | ||
图片预览




文档简介
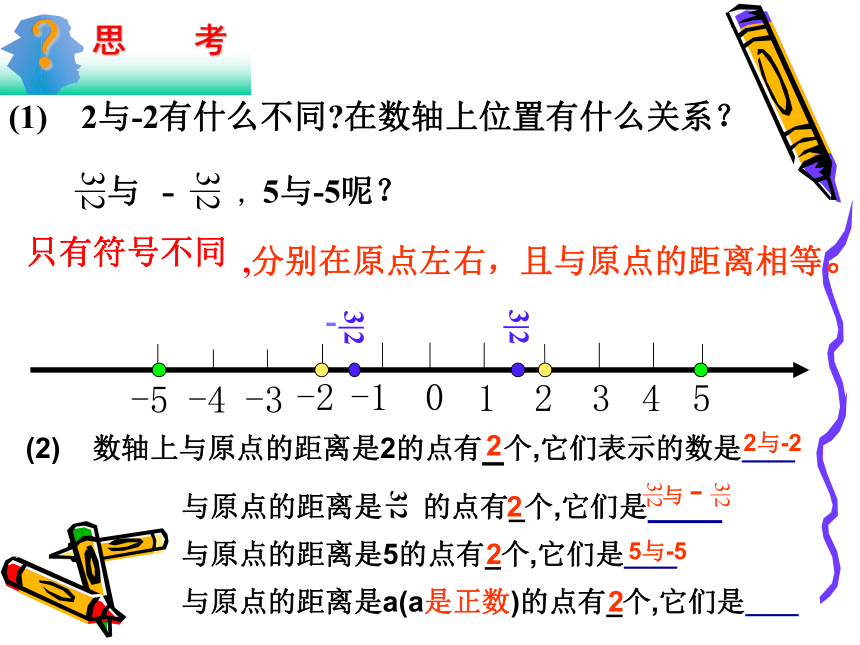
课件10张PPT。相 反 数1.2.3 相 反数(opposite number)(1) 2与-2有什么不同?在数轴上位置有什么关系?,5与-5呢?012345-5-4-3-2-13|2 ,分别在原点左右,且与原点的距离相等。(2) 数轴上与原点的距离是2的点有_个,它们表示的数是____与原点的距离是5的点有_个,它们是____与原点的距离是a(a是正数)的点有_个,它们是____22222与-25与-5只有符号不同012345-5-4-3-2-13|2 一般地,设是a一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示-a和a,我们说这两点关于原点对称.只有符号不同的两个数叫做互为相反数(opposite number)。a-a一般地,a和-a互为相反数.特别地,0的相反数是0。 在数轴上,表示相反数的两个点,分别在原点左右,与原点的距离相等,且这两点关于原点对称.归纳 ?
1:(1)分别写出下列各数的相反数;
5,-9,6.3,+11.5,
(2)指出一2.4与5各是什么数的相反数? 在一个正数前面加上一个“-”号即是正数的相 反数.在任意一个数前面加上一个“-”号,新的数是原数的相 反数. 解: 5的相反数是-5;-9的相反数是96.3的相反数是-6.3;+11.5的相反数是-11.5解: -2.4是2.4的相反数;5是-5的相反数;-(-9)=9;-(+11.5)=-11.5;2: 简化-(+3),-(-4),-[-(+6)],
-[-(-5)]的符号.解: -(+3)=-3;-(-4)=4;-[-(+6)]=6;-[-(-5)]=-5; 课堂练习:
1、填空: (1)+1.3的相反数是 ; (2) –3的相反数是 ; (3) 的相反数是一1.7;(4) 的相反数是12; (5)-(+4)是 的相反数; (6)-(-7)是 的相反数。
2. 简化下列各数的符号:
(1)-(-16); (2)-(+20);
(3)-(-3.57); (4)-[-(+3)];
(5)+[-(-1)]; (6)-[-(-5.73)].-1.331.7-124-73.下列两对数中,哪对是相等的数?哪对互为相反数?
-(-8)与+(-8); -(+8)与+(-8).
4 .填空:
(1) 如果a=-13,那么-a= ; (2)如果a=-5.4,那么-a= ; (3)如果-x=-6,那么x= ; (4)如果-x=9,那么x= ;
135.46-9 注意:当字母a表示有理数时,-a不一定就是负数。
若a 为正数,-a就是负数;
若a 为0,则-a也为0;
若a 为负数,-a就是正数;
-a只表示是有理数 a的相反数。 小结本节课学习的主要内容:
一、理解相反数的定义──代数定义与几何定义;
二、求a的相反数;
三、简化多重符号的问题.概括:在数轴上的原点两旁,离开原点距离相等的两个点所表示的数互为相反数。
只有符号不同的两个数称互为相反数。
0既不是正数,也不是负数,它到原点的距离就是0,这是相反数等于它本身的唯一的数.
1:(1)分别写出下列各数的相反数;
5,-9,6.3,+11.5,
(2)指出一2.4与5各是什么数的相反数? 在一个正数前面加上一个“-”号即是正数的相 反数.在任意一个数前面加上一个“-”号,新的数是原数的相 反数. 解: 5的相反数是-5;-9的相反数是96.3的相反数是-6.3;+11.5的相反数是-11.5解: -2.4是2.4的相反数;5是-5的相反数;-(-9)=9;-(+11.5)=-11.5;2: 简化-(+3),-(-4),-[-(+6)],
-[-(-5)]的符号.解: -(+3)=-3;-(-4)=4;-[-(+6)]=6;-[-(-5)]=-5; 课堂练习:
1、填空: (1)+1.3的相反数是 ; (2) –3的相反数是 ; (3) 的相反数是一1.7;(4) 的相反数是12; (5)-(+4)是 的相反数; (6)-(-7)是 的相反数。
2. 简化下列各数的符号:
(1)-(-16); (2)-(+20);
(3)-(-3.57); (4)-[-(+3)];
(5)+[-(-1)]; (6)-[-(-5.73)].-1.331.7-124-73.下列两对数中,哪对是相等的数?哪对互为相反数?
-(-8)与+(-8); -(+8)与+(-8).
4 .填空:
(1) 如果a=-13,那么-a= ; (2)如果a=-5.4,那么-a= ; (3)如果-x=-6,那么x= ; (4)如果-x=9,那么x= ;
135.46-9 注意:当字母a表示有理数时,-a不一定就是负数。
若a 为正数,-a就是负数;
若a 为0,则-a也为0;
若a 为负数,-a就是正数;
-a只表示是有理数 a的相反数。 小结本节课学习的主要内容:
一、理解相反数的定义──代数定义与几何定义;
二、求a的相反数;
三、简化多重符号的问题.概括:在数轴上的原点两旁,离开原点距离相等的两个点所表示的数互为相反数。
只有符号不同的两个数称互为相反数。
0既不是正数,也不是负数,它到原点的距离就是0,这是相反数等于它本身的唯一的数.
