等式和它的性质[上学期]
文档属性
| 名称 | 等式和它的性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 195.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-24 05:44:00 | ||
图片预览











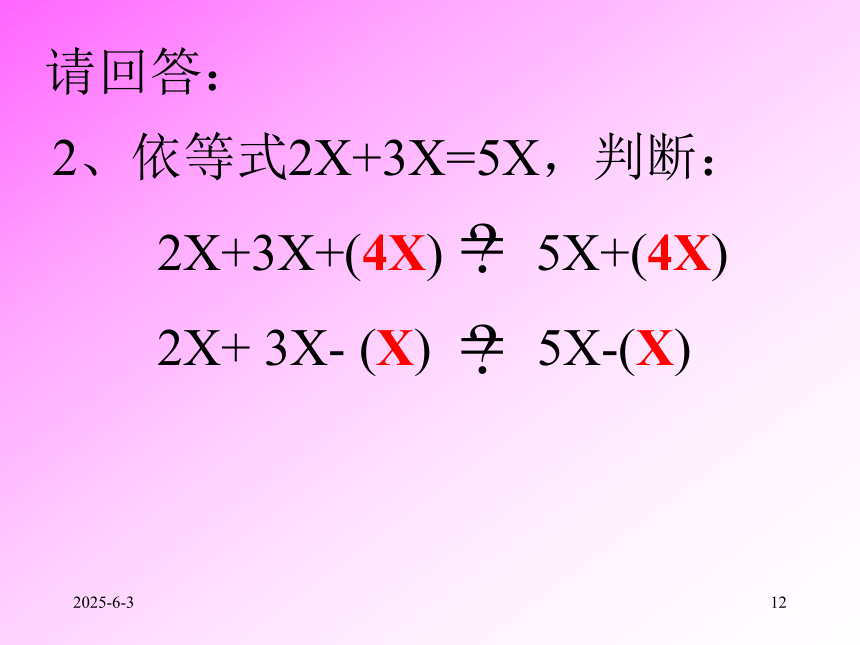
文档简介
课件75张PPT。2019/3/151第四章 一元一次方程4.1等式和它的性质制作人 :符婕2019/3/152教学目标:
1.使学生能说出等式的意义,并能举出例子,会区别等式与代数式;能说出等式的两条性质,会利用它们将简单的等式变形.
2.培养学生观察,分析 ,概括的能力.
3.初步渗透特殊到一般的辩证唯物主义思想.2019/3/153
教学重点:等式的意义和性质.
教学难点:由具体、实际问 题 抽象出等式 的性质。2019/3/154定义:用等号来表示相等关系的式子叫做等式。2019/3/155问题:下列两组式子哪些是代数式,哪些等式?2. 1+2=3, a+b=b+a, s=1/2ah, c=2πr.
4+x=7, 1/2x=5, 3x-7=5x+82019/3/156请回答:2019/3/157
1+2+(4)= 3+(4);
1+ 2 - (5) = 3 - (5)答2019/3/1582019/3/159
1+2+(-4)= 3+(-4);
1+ 2 - (-5) = 3 - (-5)答2019/3/15102019/3/1511
1+2+(0)= 3+(0);
1+ 2 - (0) = 3 - (0)答2019/3/1512请回答:2019/3/1513
2X+3X+(4X)=5X+(4X)
2X+3X - (X) =5X - (X)答2019/3/1514请回答:2019/3/1515
2X+3X+(-4X)=5X+(-4X)
2X+3X - (-X) =5X - (-X)答2019/3/1516
1+2+(4)= 3+(4);
1+ 2 - (5) = 3 - (5)
1+2+(-4)= 3+(-4);
1+ 2 - (-5) = 3 - (-5)
1+2+(0)= 3+(0);
1+ 2 - (0) = 3 - (0)2019/3/1517
2X+3X+(4X)=5X+(4X)
2X+3X - (X) =5X - (X)
2X+3X+(-4X)=5X+(-4X)
2X+3X - (-X) =5X - (-X)2019/3/1518上述两个问题反映出等式具有什么性质?性质1 :等式的两边都加上 (或减去)同一个数或同一个整式,所得的结果仍是等式。2019/3/1519再来看:
2019/3/1520答2×(3M+5M)= 2×8M
(3M+5M)÷2 = 8M÷2
2019/3/15212019/3/1522答-2×(3M+5M)= -2×8M
(3M+5M)÷(-2) = 8M÷(-2)
2019/3/15232019/3/1524答0×(3M+5M)= 0×8M0不能做除数!2019/3/15252×(3M+5M)= 2×8M
(3M+5M)÷2 = 8M÷2
-2×(3M+5M)= -2×8M
(3M+5M)÷(-2) = 8M÷(-2)
0×(3M+5M)= 0×8M0不能做除数!2019/3/1526上述问题反映出等式具有什么性质?性质2:等式的两边都乘以 (或除以)同一个数(除数不为零),所得的结果仍是等式。2019/3/1527^_^2019/3/1528^_^2019/3/1529^_^2019/3/1530^_^2019/3/1531^_^2019/3/1532^_^2019/3/1533^_^2019/3/1534^_^2019/3/1535^_^2019/3/1536^_^2019/3/1537^_^2019/3/1538^_^2019/3/1539^_^2019/3/1540^_^2019/3/1541^_^2019/3/1542^_^2019/3/1543^_^2019/3/1544^_^2019/3/1545^_^^_^2019/3/1546^_^2019/3/1547^_^2019/3/1548^_^2019/3/1549^_^2019/3/1550^_^2019/3/1551^_^2019/3/1552^_^2019/3/1553^_^2019/3/1554^_^2019/3/1555^_^^_^2019/3/1556这个事实充分说明,等式具备上边那两条性质.2019/3/1557用数学符号语言表示:性质: 1 若a=b,则a+m=b+m.性质: 22019/3/1558应用举例,变式练习例1 若a=b,怎样得到下列等式?(1) a-3=b-3(2) -a=-b(3) 3a=3b(4) -1/2a=-1/2b(5) 0a=0b2019/3/1559问:条件和结论互换后,是否还成立?2019/3/1560则a=b则a=b则a=b则a=b则a=b不一定
成立2019/3/1561例2:用适当的数或整式填空,使所 得的结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形的.(1) 若2x=5-3x,则2x+__=5;3x(2) 若0.2x=1,则x=__52019/3/1562例3:运用等式性质求出下列方程中未知数的值:(1) 5x-7=8解:(1)运用等式性质1,方程两边都加上7,即5x-7+7=8+7得5x=15,运用等式性质2,方程两边都除以5得x=3.2019/3/1563(2) 2x+4=-6解:(2)运用等式性质1,方程两边都减去4,即2x+4-4=-6-4得2x=-10,运用等式性质2,方程两边都除以2得x=-5.2019/3/1564课堂练习:1.从x=y能否得到x+5=y+5?为什么?2.从x=y能否得到x/9=y/9?为什么?3.从a+2=b+2能否得到a=b?4.从-3a=-3b能否得到a=b?2019/3/15655.怎样从等式5x=4x+3得到x=3?6.怎样从等式4x=12得到x=3?7.怎样从等式a/10=b/10得到a=b?8.怎样从等式2πR=2πr得到R=r?2019/3/1566小结1.本节课学习了哪些主要内容?2.运用等式性质需要注意什么?2019/3/15671.对于等式性质得导出,采用了由特殊到一般再到特殊的思维方法,它是一种非常重要的数学思维方法.总结2019/3/15682.等式可能不成立.
如x +1=0是等式,但它 不成立.23. 请大家再复述等式性质.2019/3/1569思考:1.若x=y,下列等式哪些是成立的?(1) 2x=2y(3)2x-3=2y-3(4)(x-y)x=y(x-y)(5)x/(x-y)=y/(x-y)(6)x/y=12019/3/15702.用适当的数或整式填空,使所得的结果仍是等式,并说明根据等式的哪一条性质以及怎样变形的.(1)若5x=4x+7,则5x-___=7(2)若-3y=18,则y=___2019/3/1571(3)若2a=1.5,则6a=___(4)若a+8=b+8,则a=___(5)若-5x=5y,则x=___2019/3/15723.根据等式性质,把下列等式变成左边只剩下字母x,右边只是一个数的等式.(1)x+3=10(2)3x=-9(3)2x+7=15(4)4-0.5x=52019/3/1573^_^2019/3/1574^_^2019/3/1575
1.使学生能说出等式的意义,并能举出例子,会区别等式与代数式;能说出等式的两条性质,会利用它们将简单的等式变形.
2.培养学生观察,分析 ,概括的能力.
3.初步渗透特殊到一般的辩证唯物主义思想.2019/3/153
教学重点:等式的意义和性质.
教学难点:由具体、实际问 题 抽象出等式 的性质。2019/3/154定义:用等号来表示相等关系的式子叫做等式。2019/3/155问题:下列两组式子哪些是代数式,哪些等式?2. 1+2=3, a+b=b+a, s=1/2ah, c=2πr.
4+x=7, 1/2x=5, 3x-7=5x+82019/3/156请回答:2019/3/157
1+2+(4)= 3+(4);
1+ 2 - (5) = 3 - (5)答2019/3/1582019/3/159
1+2+(-4)= 3+(-4);
1+ 2 - (-5) = 3 - (-5)答2019/3/15102019/3/1511
1+2+(0)= 3+(0);
1+ 2 - (0) = 3 - (0)答2019/3/1512请回答:2019/3/1513
2X+3X+(4X)=5X+(4X)
2X+3X - (X) =5X - (X)答2019/3/1514请回答:2019/3/1515
2X+3X+(-4X)=5X+(-4X)
2X+3X - (-X) =5X - (-X)答2019/3/1516
1+2+(4)= 3+(4);
1+ 2 - (5) = 3 - (5)
1+2+(-4)= 3+(-4);
1+ 2 - (-5) = 3 - (-5)
1+2+(0)= 3+(0);
1+ 2 - (0) = 3 - (0)2019/3/1517
2X+3X+(4X)=5X+(4X)
2X+3X - (X) =5X - (X)
2X+3X+(-4X)=5X+(-4X)
2X+3X - (-X) =5X - (-X)2019/3/1518上述两个问题反映出等式具有什么性质?性质1 :等式的两边都加上 (或减去)同一个数或同一个整式,所得的结果仍是等式。2019/3/1519再来看:
2019/3/1520答2×(3M+5M)= 2×8M
(3M+5M)÷2 = 8M÷2
2019/3/15212019/3/1522答-2×(3M+5M)= -2×8M
(3M+5M)÷(-2) = 8M÷(-2)
2019/3/15232019/3/1524答0×(3M+5M)= 0×8M0不能做除数!2019/3/15252×(3M+5M)= 2×8M
(3M+5M)÷2 = 8M÷2
-2×(3M+5M)= -2×8M
(3M+5M)÷(-2) = 8M÷(-2)
0×(3M+5M)= 0×8M0不能做除数!2019/3/1526上述问题反映出等式具有什么性质?性质2:等式的两边都乘以 (或除以)同一个数(除数不为零),所得的结果仍是等式。2019/3/1527^_^2019/3/1528^_^2019/3/1529^_^2019/3/1530^_^2019/3/1531^_^2019/3/1532^_^2019/3/1533^_^2019/3/1534^_^2019/3/1535^_^2019/3/1536^_^2019/3/1537^_^2019/3/1538^_^2019/3/1539^_^2019/3/1540^_^2019/3/1541^_^2019/3/1542^_^2019/3/1543^_^2019/3/1544^_^2019/3/1545^_^^_^2019/3/1546^_^2019/3/1547^_^2019/3/1548^_^2019/3/1549^_^2019/3/1550^_^2019/3/1551^_^2019/3/1552^_^2019/3/1553^_^2019/3/1554^_^2019/3/1555^_^^_^2019/3/1556这个事实充分说明,等式具备上边那两条性质.2019/3/1557用数学符号语言表示:性质: 1 若a=b,则a+m=b+m.性质: 22019/3/1558应用举例,变式练习例1 若a=b,怎样得到下列等式?(1) a-3=b-3(2) -a=-b(3) 3a=3b(4) -1/2a=-1/2b(5) 0a=0b2019/3/1559问:条件和结论互换后,是否还成立?2019/3/1560则a=b则a=b则a=b则a=b则a=b不一定
成立2019/3/1561例2:用适当的数或整式填空,使所 得的结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形的.(1) 若2x=5-3x,则2x+__=5;3x(2) 若0.2x=1,则x=__52019/3/1562例3:运用等式性质求出下列方程中未知数的值:(1) 5x-7=8解:(1)运用等式性质1,方程两边都加上7,即5x-7+7=8+7得5x=15,运用等式性质2,方程两边都除以5得x=3.2019/3/1563(2) 2x+4=-6解:(2)运用等式性质1,方程两边都减去4,即2x+4-4=-6-4得2x=-10,运用等式性质2,方程两边都除以2得x=-5.2019/3/1564课堂练习:1.从x=y能否得到x+5=y+5?为什么?2.从x=y能否得到x/9=y/9?为什么?3.从a+2=b+2能否得到a=b?4.从-3a=-3b能否得到a=b?2019/3/15655.怎样从等式5x=4x+3得到x=3?6.怎样从等式4x=12得到x=3?7.怎样从等式a/10=b/10得到a=b?8.怎样从等式2πR=2πr得到R=r?2019/3/1566小结1.本节课学习了哪些主要内容?2.运用等式性质需要注意什么?2019/3/15671.对于等式性质得导出,采用了由特殊到一般再到特殊的思维方法,它是一种非常重要的数学思维方法.总结2019/3/15682.等式可能不成立.
如x +1=0是等式,但它 不成立.23. 请大家再复述等式性质.2019/3/1569思考:1.若x=y,下列等式哪些是成立的?(1) 2x=2y(3)2x-3=2y-3(4)(x-y)x=y(x-y)(5)x/(x-y)=y/(x-y)(6)x/y=12019/3/15702.用适当的数或整式填空,使所得的结果仍是等式,并说明根据等式的哪一条性质以及怎样变形的.(1)若5x=4x+7,则5x-___=7(2)若-3y=18,则y=___2019/3/1571(3)若2a=1.5,则6a=___(4)若a+8=b+8,则a=___(5)若-5x=5y,则x=___2019/3/15723.根据等式性质,把下列等式变成左边只剩下字母x,右边只是一个数的等式.(1)x+3=10(2)3x=-9(3)2x+7=15(4)4-0.5x=52019/3/1573^_^2019/3/1574^_^2019/3/1575
