余角和补角(1)[上学期]
文档属性
| 名称 | 余角和补角(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 602.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-18 00:00:00 | ||
图片预览






文档简介
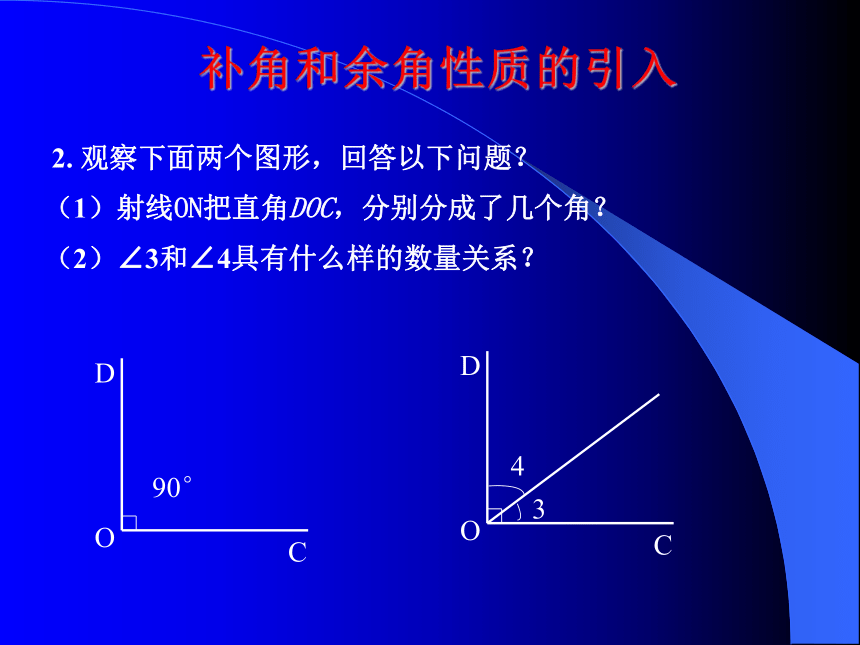
课件15张PPT。新课标七年级数学教学交 流 课2005年12月 4 日镇远县羊场中学数学教研组3.4.2 余角和补角⑴补角和余角性质的引入1. 观察下面两个图形,回答以下问题?(1)射线 OM 把平角∠AOB,分别分成了几个角?(2)∠1和∠2具有什么样的数量关系?补角和余角性质的引入2. 观察下面两个图形,回答以下问题?(1)射线ON把直角DOC,分别分成了几个角?(2)∠3和∠4具有什么样的数量关系?补角和余角性质的小结 结论:不论∠1、∠2、∠3、∠4的位置关系如何变化,只要大小不变, ∠1与∠2的和永远是平角, ∠3与∠4的和永远是直角。像这样具有特殊关系的角,我们分别叫它们互为补角和互为余角。互为余角、互为补角的定义 你能根据前面的演示和说明,叙述一下具有什么关系的两个角叫互为余角和互为补角吗?1.互为余角的定义 :如果两个角的和是一个直角,那么这两个角叫互为余角.其中一个角叫做另一个角的余角。2.互为补角的定义 :如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角。问题1问题3:互为余角、互为补角的两个角是否一定有公共顶点? :以上定义中的“互为”是什么意思?问题2:若 ,那么∠1、∠2、∠3互为
补角吗? 练习:如图,O是直线AB上一点,OC是∠AOB的平分线
①∠AOD的补角是____________
②∠AOD的余角是____________
③∠DOB的补角是____________教学例题1例:如图,已知∠AOC = 108°, ∠BOC = 36°试判断图
中哪两个角互为补角。教学例题2已知一个角的余角是它的补角的三分之一,求这个角。练 习 1已知∠α与∠β 互余,且∠α比∠β 小
25°,求2 ∠α— ∠β 的值。教学例题3问题:如下图,∠1与∠2互补,∠3与∠4互补,如果
∠1=∠3,那么∠2=∠4成立吗?分析:由∠1与∠2互补,可得∠2 =180°- 。
∠3与∠4互补,可得∠4 =180°- 。总 结由上例我们可以知道以下重要性质:
等角的补角相等;等角的余角相等。练 习 2如图,已知∠1 +∠2 = 90°, ∠2 +∠3= 90°问∠1 与∠3有什么关系?为什么?若要∠2 与∠4
相等 ,则∠1 与∠4要满足什么关系?为什么?作业P139:第6题(书)
P140:第10题(作业本)思考题
1.锐角的余角一定是锐角吗?
2.一个锐角和一个钝角一定互为补角吗?
3.一个角的补角比这个角的余角大多少度?
4.相等且互补的两个角各是多少度?
5.一个角的补角一定比这个角大吗?镇远县羊场中学数学教研组 潘清勇敬请指正
补角吗? 练习:如图,O是直线AB上一点,OC是∠AOB的平分线
①∠AOD的补角是____________
②∠AOD的余角是____________
③∠DOB的补角是____________教学例题1例:如图,已知∠AOC = 108°, ∠BOC = 36°试判断图
中哪两个角互为补角。教学例题2已知一个角的余角是它的补角的三分之一,求这个角。练 习 1已知∠α与∠β 互余,且∠α比∠β 小
25°,求2 ∠α— ∠β 的值。教学例题3问题:如下图,∠1与∠2互补,∠3与∠4互补,如果
∠1=∠3,那么∠2=∠4成立吗?分析:由∠1与∠2互补,可得∠2 =180°- 。
∠3与∠4互补,可得∠4 =180°- 。总 结由上例我们可以知道以下重要性质:
等角的补角相等;等角的余角相等。练 习 2如图,已知∠1 +∠2 = 90°, ∠2 +∠3= 90°问∠1 与∠3有什么关系?为什么?若要∠2 与∠4
相等 ,则∠1 与∠4要满足什么关系?为什么?作业P139:第6题(书)
P140:第10题(作业本)思考题
1.锐角的余角一定是锐角吗?
2.一个锐角和一个钝角一定互为补角吗?
3.一个角的补角比这个角的余角大多少度?
4.相等且互补的两个角各是多少度?
5.一个角的补角一定比这个角大吗?镇远县羊场中学数学教研组 潘清勇敬请指正
