人教版高中数学必修第一册3.1.1正整数指数函数 授课课件(共21张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册3.1.1正整数指数函数 授课课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 15:44:26 | ||
图片预览








文档简介
(共21张PPT)
第三章 指数函数和对数函数
§1 正整数指数函数
1.了解正整数指数函数模型的实际背景;
2.了解正整数指数函数的概念;
3.理解具体的正整数指数函数的图像特征及其单调性.
问题导学
题型探究
达标检测
学习目标
知识点一 正整数指数函数的概念
思考 定义在N+上的函数对应关系如下,试写出其解析式,并指出自变量位置.
答案
问题导学 新知探究 点点落实
x 1 2 3 4 5 6 7 8 …
y 2 4 8 16 32 64 128 256 …
答案 y=2x,x∈N+,自变量在指数上.
一般地,正整数指数函数的定义:
形如y=ax(a>0,a≠1,x∈N+)的函数,其中x是自变量,定义域是正整数集N+.
知识点二 正整数指数函数的图像特征及其单调性
思考 韦伯对一个叫杰米的百万富翁说,我想和你定个合同,我将在整整一个月中每天给你10万元,而你第一天只需给我一分钱,以后每一天给我的钱是前一天的两倍.杰米想:要是合同定两个月、三个月该多好!事情真的如杰米想的一样吗?
答案 到第28天,杰米支出227=134 217 728(分)≈134.218(万元),
收入还是10万,已经远比收入多了.
一般地,函数y=ax(a>0,a≠1,x∈N+)图像是散点图,当a>1时,在定义域上递增;当0答案
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 正整数指数函数的概念
例1 下列表达式是否为正整数指数函数?
(1)y=1x;(2)y=(-2)x;(3)y=3-x(x∈R);(4)y=ex(x∈N+).
解 (1)(2)底数不符合,要大于0且不等于1,
但定义域不符合,所以只有(4)为正整数指数函数.
反思与感悟 判断函数是否为正整数指数函数,应注意函数形式是否符合,特别还应看定义域是否为正整数集.
解析答案
跟踪训练1 下列函数中是正整数指数函数的是( )
A.y=-2x,x∈N+
B.y=2x,x∈R
C.y=x2,x∈N+
D.y=( )x,x∈N+
解析 结合正整数指数函数的定义,选D.
D
解析答案
类型二 正整数指数函数的图像与性质
例2 比较下面两个正整数指数函数的图像与性质:
(1)y=2x(x∈N+);
(2)y=0.997 520x(x∈N+).
反思与感悟
解析答案
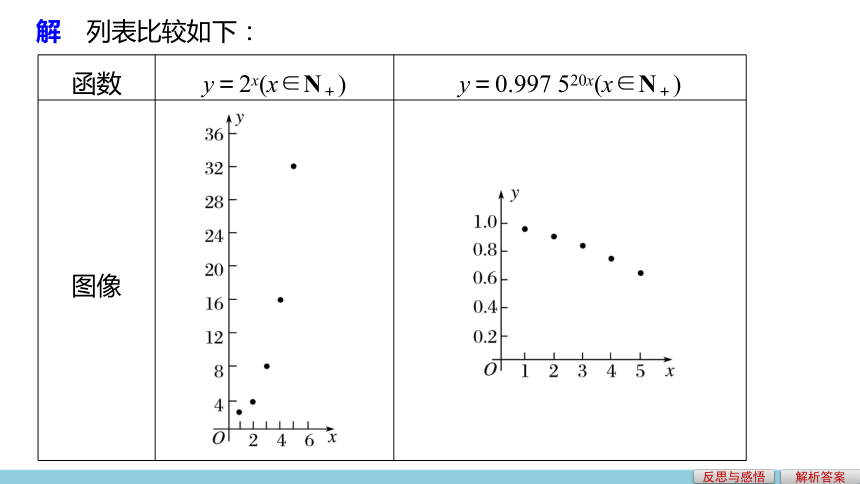
解 列表比较如下:
函数 y=2x(x∈N+) y=0.997 520x(x∈N+)
图像
反思与感悟
定义域 正整数集N+ 单调性 增函数 减函数
图像特征 一群孤立的点组成 反思与感悟
反思与感悟
通过列表、描点画图,即可得到正整数指数函数的图像,由于定义域为正整数集,所以不需要连成光滑曲线,图像就是由一群孤立的点组成.
解析答案
跟踪训练2 作出下列函数(x∈N+)的图像:
(1)y=3x;
解
解
解析答案
类型三 正整数指数函数的应用
例3 某种储蓄按复利计算利息,若本金为a元,每期利率为r,设存期是x,本利和(本金加上利息)为y元.
(1)写出本利和y随存期x变化的函数关系式;
解 已知本金为a元,利率为r,
则1期后的本利和为y=a+a×r=a(1+r),
2期后的本利和为y=a(1+r)+a(1+r)r=a(1+r)2,
3期后的本利和为y=a(1+r)3,
x期后的本利和为y=a(1+r)x,x∈N+,
即本利和y随存期x变化的函数关系式为y=a(1+r)x,x∈N+.
解析答案
(2)如果存入本金1 000元,每期利率为2.25%,试计算5期后的本利和.
解 将a=1 000(元),r=2.25%,x=5代入上式,
得y=1 000×(1+2.25%)5=1 000×1.022 55≈1 117.68(元),
即5期后本利和约为1 117.68元.
反思与感悟 在实际问题中,经常会遇到类似本例中的指数增长模型:设原有量为N,平均增长率为p,则对于经过时间x后的总量y可以用y=N(1+p)x表示,我们把形如y=kax(k∈R,a>0且a≠1)的函数称为指数型函数,这是非常有用的函数模型.
反思与感悟
跟踪训练3 一个人喝了少量酒后血液中酒精含量迅速上升到0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时50%的速度减少.为了保障交通安全,某地交通规则规定,驾驶员血液中酒精含量不得超过0.08 mg/mL.问喝了少量酒的驾驶员,至少过几小时才能驾驶?(精确到1小时)
解 1小时后驾驶员血液中的酒精含量为0.3(1-50%) mg/mL,
x小时后其酒精含量为0.3(1-50%)x mg/mL.
所以满足要求的x的最小整数为2,故至少过2小时驾驶员才能驾驶.
解析答案
返回
1
2
3
解析答案
达标检测
4
1.已知正整数指数函数f(x)=(a-2)ax,则f(2)等于( )
A.2 B.3
C.9 D.16
5
∴f(x)=3x(x∈N+),∴f(2)=32=9,故选C.
C
解析答案
2.当x∈N+时,函数y=(a-1)x的值总大于1,则实数a的取值范围是( )
A.1C.a>1 D.a>2
解析 在y=(a-1)x中,当x=0时,y=1.
而x∈N+时,y>1,则必有a-1>1,∴a>2,故选D.
1
2
3
4
5
D
解析答案
3.某商品价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来价格比较,变化情况是( )
A.增加7.84% B.减少7.84%
C.减少9.5% D.不增不减
解析 设商品原价为a,两年后价格为a(1+20%)2,
四年后价格为a(1+20%)2(1-20%)2=a(1-0.04)2=0.921 6a,
1
2
3
4
5
B
解析答案
4.由于生产电脑的成本不断降低,若每年电脑价格降低 ,设现在的电脑价格为8 100元,则3年后的价格可降为( )
A.2 400元 B.2 700元
C.3 000元 D.3 600元
1
2
3
4
5
A
解析答案
5.正整数指数函数f(x)=(a-2)(2a)x(x∈N+)在定义域N+上是 的.
(填“增加”或“减少”)
解析 ∵f(x)=(a-2)(2a)x是正整数指数函数,
∴a-2=1,且2a>0,2a≠1,
∴a=3,∴f(x)=6x,x∈N+.
∵6>1,∴f(x)在N+上是增加的.
1
2
3
4
5
增加
返回
规律与方法
1.判断函数是否为正整数指数函数,应注意函数形式和定义域是否为正整数集.
2.当a>1时是单调递增函数.
3.当04.正整数指数函数的图像是一些孤立的点.
本课结束
第三章 指数函数和对数函数
§1 正整数指数函数
1.了解正整数指数函数模型的实际背景;
2.了解正整数指数函数的概念;
3.理解具体的正整数指数函数的图像特征及其单调性.
问题导学
题型探究
达标检测
学习目标
知识点一 正整数指数函数的概念
思考 定义在N+上的函数对应关系如下,试写出其解析式,并指出自变量位置.
答案
问题导学 新知探究 点点落实
x 1 2 3 4 5 6 7 8 …
y 2 4 8 16 32 64 128 256 …
答案 y=2x,x∈N+,自变量在指数上.
一般地,正整数指数函数的定义:
形如y=ax(a>0,a≠1,x∈N+)的函数,其中x是自变量,定义域是正整数集N+.
知识点二 正整数指数函数的图像特征及其单调性
思考 韦伯对一个叫杰米的百万富翁说,我想和你定个合同,我将在整整一个月中每天给你10万元,而你第一天只需给我一分钱,以后每一天给我的钱是前一天的两倍.杰米想:要是合同定两个月、三个月该多好!事情真的如杰米想的一样吗?
答案 到第28天,杰米支出227=134 217 728(分)≈134.218(万元),
收入还是10万,已经远比收入多了.
一般地,函数y=ax(a>0,a≠1,x∈N+)图像是散点图,当a>1时,在定义域上递增;当0
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 正整数指数函数的概念
例1 下列表达式是否为正整数指数函数?
(1)y=1x;(2)y=(-2)x;(3)y=3-x(x∈R);(4)y=ex(x∈N+).
解 (1)(2)底数不符合,要大于0且不等于1,
但定义域不符合,所以只有(4)为正整数指数函数.
反思与感悟 判断函数是否为正整数指数函数,应注意函数形式是否符合,特别还应看定义域是否为正整数集.
解析答案
跟踪训练1 下列函数中是正整数指数函数的是( )
A.y=-2x,x∈N+
B.y=2x,x∈R
C.y=x2,x∈N+
D.y=( )x,x∈N+
解析 结合正整数指数函数的定义,选D.
D
解析答案
类型二 正整数指数函数的图像与性质
例2 比较下面两个正整数指数函数的图像与性质:
(1)y=2x(x∈N+);
(2)y=0.997 520x(x∈N+).
反思与感悟
解析答案
解 列表比较如下:
函数 y=2x(x∈N+) y=0.997 520x(x∈N+)
图像
反思与感悟
定义域 正整数集N+ 单调性 增函数 减函数
图像特征 一群孤立的点组成 反思与感悟
反思与感悟
通过列表、描点画图,即可得到正整数指数函数的图像,由于定义域为正整数集,所以不需要连成光滑曲线,图像就是由一群孤立的点组成.
解析答案
跟踪训练2 作出下列函数(x∈N+)的图像:
(1)y=3x;
解
解
解析答案
类型三 正整数指数函数的应用
例3 某种储蓄按复利计算利息,若本金为a元,每期利率为r,设存期是x,本利和(本金加上利息)为y元.
(1)写出本利和y随存期x变化的函数关系式;
解 已知本金为a元,利率为r,
则1期后的本利和为y=a+a×r=a(1+r),
2期后的本利和为y=a(1+r)+a(1+r)r=a(1+r)2,
3期后的本利和为y=a(1+r)3,
x期后的本利和为y=a(1+r)x,x∈N+,
即本利和y随存期x变化的函数关系式为y=a(1+r)x,x∈N+.
解析答案
(2)如果存入本金1 000元,每期利率为2.25%,试计算5期后的本利和.
解 将a=1 000(元),r=2.25%,x=5代入上式,
得y=1 000×(1+2.25%)5=1 000×1.022 55≈1 117.68(元),
即5期后本利和约为1 117.68元.
反思与感悟 在实际问题中,经常会遇到类似本例中的指数增长模型:设原有量为N,平均增长率为p,则对于经过时间x后的总量y可以用y=N(1+p)x表示,我们把形如y=kax(k∈R,a>0且a≠1)的函数称为指数型函数,这是非常有用的函数模型.
反思与感悟
跟踪训练3 一个人喝了少量酒后血液中酒精含量迅速上升到0.3 mg/mL,在停止喝酒后,血液中的酒精含量以每小时50%的速度减少.为了保障交通安全,某地交通规则规定,驾驶员血液中酒精含量不得超过0.08 mg/mL.问喝了少量酒的驾驶员,至少过几小时才能驾驶?(精确到1小时)
解 1小时后驾驶员血液中的酒精含量为0.3(1-50%) mg/mL,
x小时后其酒精含量为0.3(1-50%)x mg/mL.
所以满足要求的x的最小整数为2,故至少过2小时驾驶员才能驾驶.
解析答案
返回
1
2
3
解析答案
达标检测
4
1.已知正整数指数函数f(x)=(a-2)ax,则f(2)等于( )
A.2 B.3
C.9 D.16
5
∴f(x)=3x(x∈N+),∴f(2)=32=9,故选C.
C
解析答案
2.当x∈N+时,函数y=(a-1)x的值总大于1,则实数a的取值范围是( )
A.1
解析 在y=(a-1)x中,当x=0时,y=1.
而x∈N+时,y>1,则必有a-1>1,∴a>2,故选D.
1
2
3
4
5
D
解析答案
3.某商品价格前两年每年递增20%,后两年每年递减20%,则四年后的价格与原来价格比较,变化情况是( )
A.增加7.84% B.减少7.84%
C.减少9.5% D.不增不减
解析 设商品原价为a,两年后价格为a(1+20%)2,
四年后价格为a(1+20%)2(1-20%)2=a(1-0.04)2=0.921 6a,
1
2
3
4
5
B
解析答案
4.由于生产电脑的成本不断降低,若每年电脑价格降低 ,设现在的电脑价格为8 100元,则3年后的价格可降为( )
A.2 400元 B.2 700元
C.3 000元 D.3 600元
1
2
3
4
5
A
解析答案
5.正整数指数函数f(x)=(a-2)(2a)x(x∈N+)在定义域N+上是 的.
(填“增加”或“减少”)
解析 ∵f(x)=(a-2)(2a)x是正整数指数函数,
∴a-2=1,且2a>0,2a≠1,
∴a=3,∴f(x)=6x,x∈N+.
∵6>1,∴f(x)在N+上是增加的.
1
2
3
4
5
增加
返回
规律与方法
1.判断函数是否为正整数指数函数,应注意函数形式和定义域是否为正整数集.
2.当a>1时是单调递增函数.
3.当0
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
