二元一次方程[上学期]

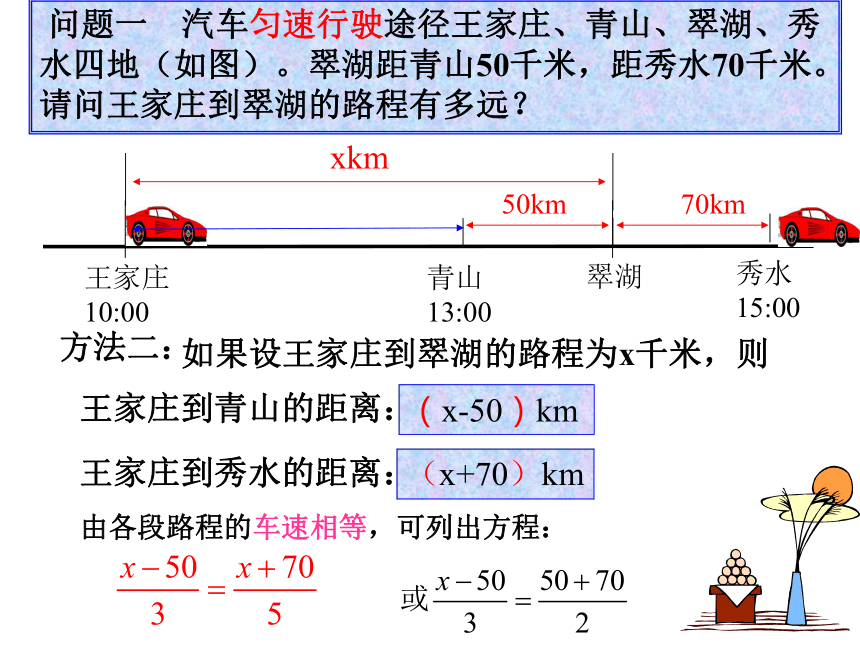
课件15张PPT。2.1.1 一元一次方程（1） 问题一： 汽车匀速行驶途径王家庄、青山、翠湖、秀水四地（如图）。翠湖距青山50千米，距秀水70千米。请问王家庄到翠湖的路程有多远？方法一：　（50＋70）÷2×3＋50（50＋70）÷2×5－70你会用其他方法来解决这个问题吗？ 问题一 汽车匀速行驶途径王家庄、青山、翠湖、秀水四地（如图）。翠湖距青山50千米，距秀水70千米。请问王家庄到翠湖的路程有多远？王家庄到青山的距离：王家庄到秀水的距离：（x-50）km（x+70）km方法二：如果设王家庄到翠湖的路程为x千米，则由各段路程的车速相等，可列出方程：问题二：一位种粮大户，今年粮食产量为10万千克，他引进了新品种，粮食产量以20%的增长率增长，则明年的粮食产量为多少千克？后年呢？变题：一位种粮食大户，今年粮食产量为10万千克，他引进了新品种，粮食产量每年以相同的增长率增长，并且到后年粮食产量达到14.4万千克，求这两年的平均增长率.你能用算术方法解决这个问题吗？明年的粮食产量为12万千克，后年为14.4万千克.解：设平均增长率为x.粮食产量(万千克)10(1+x)10(1+x)(1+x)则： 10(1+x)(1+x)=14.4列算式： 根据问题中的数量关系
列出算式，只能用到未知数； 列方程：根据问题中的等量关系列出
等式，其中既含有已知数，
又含有用字母表示的未知数；从算式到方程是数学的进步。方程-------含有未知数的等式；判断下列各式哪些是方程;根据下列问题中的条件，分别列出方程：（1）一名射击运动员，两次射击的平均成绩为6.5环，其中第二次的成绩为9环，问第一次射击的成绩是多少环？设第一次射击的成绩为x环，可列出方程　　　　　　；（2）一件衣服按8折销售的售价为72元，这件衣服的原价是多少元？设这件衣服的原价为x元，可列方程　　　　　　　　；（3）有一棵树，刚移栽时树高为2米，假设以后平均每年长0.3米，几年后树高为5米？设x年后树高为5米，可列出方程　　　　　　　　　。例1.根据下列问题，设未知数并列出方程。（1）一台计算机已使用1700小时，预计每月再使用150小时，经过多少月这台计算机的使用时间达到规定的检修时间2450小时。（2）用一根长24cm的铁丝围成一个长方形，使它的长是宽的1.5倍，长方形的长、宽各应是多少？（3）某校女生占全体学生数的52%，比男生多80人，这个学校有多少学生？实际问题方程 分析实际问题中的数量关系，利用其中的相等关系列出方程，是用数学解决实际问题的一种方法。例2.王老师利用假期带领团员同学到农村搞社会调查，每张车票原价是50元。甲车主说：“乘我的车可以打8折优惠。”；乙车主说：“乘我的车学生打9折，老师不买票。”王老师心里计算了一下，觉得不论坐谁的车，车费都一样，请问：王老师一共带了多少学生？请列出方程。解：设王老师带了x名学生由题意得：50(x+1)×0.8=50x×0.9“百羊问题” 有一位牧童赶着一群羊朝前走，另一牧童牵着一头羊从后面走来．问牧童甲：“你这群羊有多少头？有100头吗？”
　牧童甲答道：“不满100头，要是再给我这么一群
羊, 再给我这群羊的一半，再给我这群羊的
四分之一，再把你牵的一头羊也给我，才刚
好凑满100头羊．”
请问这群羊有多少头？解：设这群羊有x头由题意得：填空题1.填空：
（1）长方形的长为acm，宽为bcm，则该长方
形的周长为　 　　cm．
（2）一个三位数，个位上的数字为a，十位
上的数字为b，百位数字为c，则这个三位 数可表示为______　　　　　．2（a+b）100c+10b+a练习解答题2.设某数为x，根据下列各条件列出方程。
（1）某数的3倍比这个数大4。
（2）某数的一半与3的和等于这个数与2的差。
（3）某数的相反数比这个数的绝对值小6。
（4）某数与3的和的一半比某数的2倍与4的差
三分之一小5。
（5）比某数的2倍少9的数比它的25%大7。3x=x+4实际问题方程 分析实际问题中的数量关系，利用其中的相等关系列出方程，是用数学解决实际问题的一种方法。作业：作业本(1)