1.3.2 空间向量运算的坐标表示 课件(共15张PPT)
文档属性
| 名称 | 1.3.2 空间向量运算的坐标表示 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 16:44:18 | ||
图片预览






文档简介
(共15张PPT)
1.3.2 空间向量运算的坐标表示
人教A版高中数学选择性必修一第一章第三节
复习回顾
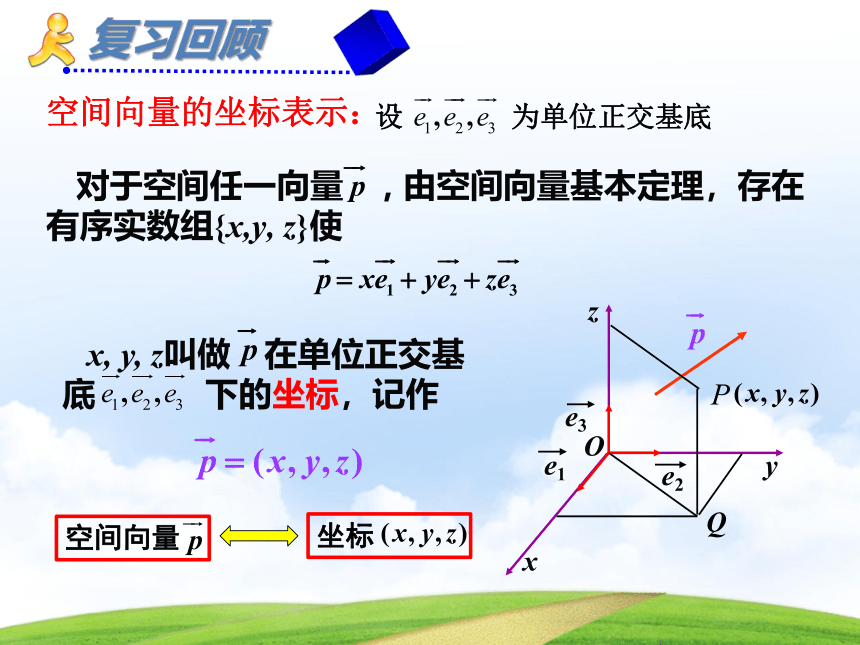
空间向量的坐标表示:
对于空间任一向量 , 由空间向量基本定理,存在有序实数组{x,y, z}使
x
y
z
O
e1
e2
e3
设 为单位正交基底
x, y, z叫做 在单位正交基底 下的坐标,记作
空间向量
坐标
加法:
减法:
数乘:
数量积:
平行:
垂直:
复习回顾
能否用坐标来表示空间向量运算呢?
平面向量 空间向量
向 量 运 算 的 坐 标 表 示 1、加减法: 2、数 乘: 3、数量积:
1、平行: 2、垂直:
1、模长: 2、夹角: 3、两点 间的距离:
类比是我们探究规律的重要方法
类比
____________
_______
____________
____________
_________
_________
____________
_______________
_________________
探究新知
1、空间向量加减法、数乘、数量积运算的坐标表示
设
加法:
减法:
数乘:
数量积:
你能对这些运算的坐标表示加以证明吗?
抓住根本:空间向量的坐标表示!
两个空间向量平行与两个平面向量平行的条件本质上是一致的,即对应坐标成比例,且比值为λ.
2、空间向量平行与垂直的坐标表示
平行:
垂直:
探究新知
3、长度、夹角、两点间距离公式
空间向量长度的几何意义表示长方体对角线的长度.
O
注意:
①
②当 时,
两向量分别同向、垂直、反向
探究新知
在空间直角坐标系中,已知点 ,则
两点间的距离
O
注意:上述公式都与坐标原点的选取无关!
探究新知
=( , -
例题分析
例题
法二:向量法
法一:几何法(定义)
例题分析
例题
【方法提炼】
①建系、读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,
获得几何结论
法一:几何法(定义)
法二:向量法
例题分析
例题
【方法提炼】
①建系、读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,
获得几何结论
法一:几何法(定义)
法二:向量法
例题分析
例题
【方法提炼】
①建系、读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,
获得几何结论
变式2:G 是 的一个靠近点B 的四等分点, H为 上的一点,若 ,试确定H点的位置.
法一:几何法(定义)
法二:向量法
演练反馈
练习
能力提升
课堂小结
1、空间向量运算的坐标表示
(1)空间向量加减、数乘、数量积运算的坐标表示
(2)平行向量、垂直向量的坐标表示,
(3)空间向量长度、夹角公式及空间两点间距离公式
2、用向量法解决立体几何问题的一般步骤
①建系,读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,获得几何结论
1.3.2 空间向量运算的坐标表示
人教A版高中数学选择性必修一第一章第三节
复习回顾
空间向量的坐标表示:
对于空间任一向量 , 由空间向量基本定理,存在有序实数组{x,y, z}使
x
y
z
O
e1
e2
e3
设 为单位正交基底
x, y, z叫做 在单位正交基底 下的坐标,记作
空间向量
坐标
加法:
减法:
数乘:
数量积:
平行:
垂直:
复习回顾
能否用坐标来表示空间向量运算呢?
平面向量 空间向量
向 量 运 算 的 坐 标 表 示 1、加减法: 2、数 乘: 3、数量积:
1、平行: 2、垂直:
1、模长: 2、夹角: 3、两点 间的距离:
类比是我们探究规律的重要方法
类比
____________
_______
____________
____________
_________
_________
____________
_______________
_________________
探究新知
1、空间向量加减法、数乘、数量积运算的坐标表示
设
加法:
减法:
数乘:
数量积:
你能对这些运算的坐标表示加以证明吗?
抓住根本:空间向量的坐标表示!
两个空间向量平行与两个平面向量平行的条件本质上是一致的,即对应坐标成比例,且比值为λ.
2、空间向量平行与垂直的坐标表示
平行:
垂直:
探究新知
3、长度、夹角、两点间距离公式
空间向量长度的几何意义表示长方体对角线的长度.
O
注意:
①
②当 时,
两向量分别同向、垂直、反向
探究新知
在空间直角坐标系中,已知点 ,则
两点间的距离
O
注意:上述公式都与坐标原点的选取无关!
探究新知
=( , -
例题分析
例题
法二:向量法
法一:几何法(定义)
例题分析
例题
【方法提炼】
①建系、读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,
获得几何结论
法一:几何法(定义)
法二:向量法
例题分析
例题
【方法提炼】
①建系、读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,
获得几何结论
法一:几何法(定义)
法二:向量法
例题分析
例题
【方法提炼】
①建系、读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,
获得几何结论
变式2:G 是 的一个靠近点B 的四等分点, H为 上的一点,若 ,试确定H点的位置.
法一:几何法(定义)
法二:向量法
演练反馈
练习
能力提升
课堂小结
1、空间向量运算的坐标表示
(1)空间向量加减、数乘、数量积运算的坐标表示
(2)平行向量、垂直向量的坐标表示,
(3)空间向量长度、夹角公式及空间两点间距离公式
2、用向量法解决立体几何问题的一般步骤
①建系,读取点坐标
②构造向量并坐标化
③进行向量的坐标运算,获得几何结论
