3.2.1单调性 课件(共30张PPT)
文档属性
| 名称 | 3.2.1单调性 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 43.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 18:21:28 | ||
图片预览









文档简介
(共30张PPT)
NEW
2023 / 07
第 3 章 函数的概念与性质
人教A版2019必修第一册
3.2.1 函数的单调性
01.
分段函数求值
03.
分段函数图象应用
02.
分段图象
目录
学习目标
1.理解函数的单调性及其几何意义,能运用函数图象理解和研究函数的单调性.
2.会用函数单调性的定义判断(或证明)一些函数的单调性.
3.会求一些具体函数的单调区间.
Topic. 01
01 情景导入
导入
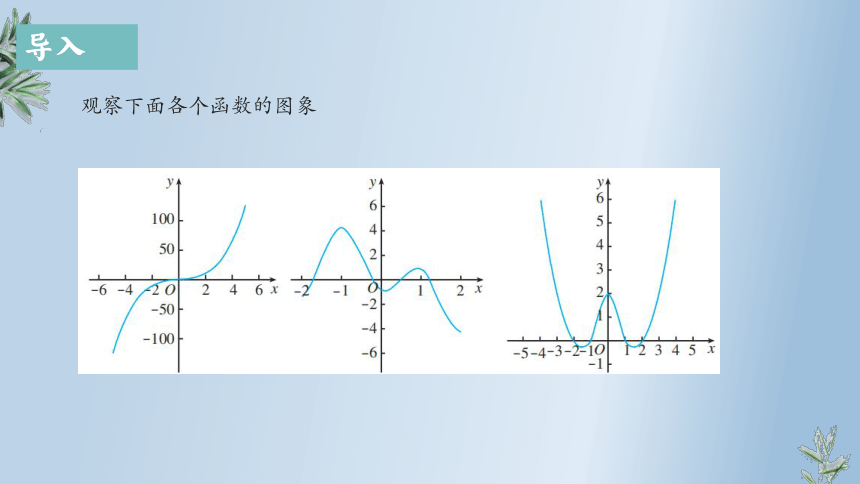
观察下面各个函数的图象
导入
问题1:函数图象都有什么特征
图一为上升趋势,图二、图三有上升也有下降趋势.
问题2:反映了函数的哪些性质?
函数值随着自变量的增大而增大(或减小)的性质,即反映了函数图象的单调性。
Topic. 02
02 函数的单调性
单调性
x
y
o
x
y
o
x
y
o
观察下面各个函数的图象的趋势
上升
下降
先上升后下降
单调性
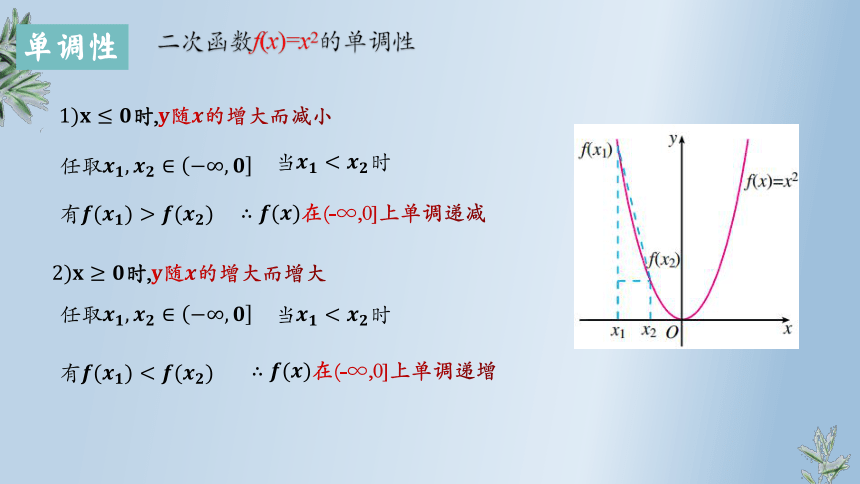
二次函数f(x)=x2的单调性
1)时,随的增大而减小
在(-∞,0]上单调递减
任取
当时
有
2)时,随的增大而增大
在(-∞,0]上单调递增
任取
当时
有
单调性
函数的定义域I,区间D,在区间D上的任意两个自变量的值
增函数
当时,都有,
那么就称函数在区间上单调递增。
减函数
当时,都有,
那么就称函数在区间上单调递减
函数单调性定义的等价形式(对于任意的 ):
(1)
在D上为增函数;
(2)
在D上为减函数;
(3)
在D上为增函数;
(4)
在D上为减函数.
单调性
单调性
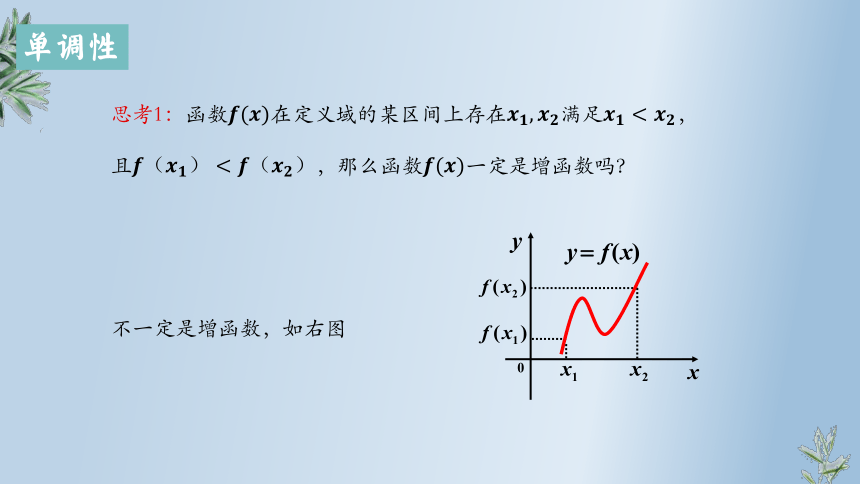
思考1:函数在定义域的某区间上存在满足,且,那么函数一定是增函数吗?
不一定是增函数,如右图
单调性
思考2:函数的单调性是对定义域内某个区间而言的,
(1)你能举出在整个定义域内是单调递增的函数例子吗?
(2)你能举出在定义域内的某些区间单调递增但在另一些区间上单调递减的函数例子吗?
1
2
3
4
5
-1
-2
-3
-4
-2
-3
2
3
o
(1)定义域内是单调递增的函数
(2)某些区间单调递增但在另一些区间上单调递减如右图
Topic. 03
03 函数单调性的证明
证明单调性
判断(证明)单调性:
单调递增
单调递减
证明单调性
1. 根据定义,研究函数 的单调性
解:函数 的定义域是R,对于任意的 且
都有
由 知 ,
这时,函数 是增函数;
当 时, ,即 ,
这时,函数 是减函数;
当 时, ,即 ,
证明单调性
用定义证明函数的单调性的步骤:
1.取数:任取x1,x2∈D,且x12.作差:f(x1)-f(x2);
3.变形:通常是因式分解和配方;
4.定号:判断差f(x1)-f(x2)的正负;
5.结论:指出函数f(x)在给定的区间D上的单调性.
证明单调性
取值
结论
变形
定号
作差
Topic. 04
04 函数单调性应用
求单调区间
1.f(x)的图像如士所示,则函数f(x)的单调递减区间是 ( )
A.(-1,0) B.(1,+∞)
C.(-1,0)∪(1,+∞) D.(-1,0),(1,+∞)
D
求单调区间
2.函数f(x)=x2-2x-3的单调增区间是__________
[变式]函数f(x)=|x2-2x-3|的单调增区间是_____________.
3函数f(x)=-x2+2|x|+1的单调减区间是_______________.
[1,+∞)
[-1,1]和[3,+∞)
[-1,0]和[1,+∞)
求单调区间
求单调区间
求单调区间
增+增=增
减+减=减
增-减=增
减-增=减
注:“增-增”、“减-减”无法确定单调性
求单调区间
4.(多选题)下列函数在 上单调递增的是( ).
A. B. C. D.
CD
应用
应用
Topic. 05
05 课堂小结
课堂小结
总结:
1.函数单调性定义。
2.函数单调性证明
3.函数单调性的应用
NEW
2023/ 07
感谢观看
NEW
2023 / 07
第 3 章 函数的概念与性质
人教A版2019必修第一册
3.2.1 函数的单调性
01.
分段函数求值
03.
分段函数图象应用
02.
分段图象
目录
学习目标
1.理解函数的单调性及其几何意义,能运用函数图象理解和研究函数的单调性.
2.会用函数单调性的定义判断(或证明)一些函数的单调性.
3.会求一些具体函数的单调区间.
Topic. 01
01 情景导入
导入
观察下面各个函数的图象
导入
问题1:函数图象都有什么特征
图一为上升趋势,图二、图三有上升也有下降趋势.
问题2:反映了函数的哪些性质?
函数值随着自变量的增大而增大(或减小)的性质,即反映了函数图象的单调性。
Topic. 02
02 函数的单调性
单调性
x
y
o
x
y
o
x
y
o
观察下面各个函数的图象的趋势
上升
下降
先上升后下降
单调性
二次函数f(x)=x2的单调性
1)时,随的增大而减小
在(-∞,0]上单调递减
任取
当时
有
2)时,随的增大而增大
在(-∞,0]上单调递增
任取
当时
有
单调性
函数的定义域I,区间D,在区间D上的任意两个自变量的值
增函数
当时,都有,
那么就称函数在区间上单调递增。
减函数
当时,都有,
那么就称函数在区间上单调递减
函数单调性定义的等价形式(对于任意的 ):
(1)
在D上为增函数;
(2)
在D上为减函数;
(3)
在D上为增函数;
(4)
在D上为减函数.
单调性
单调性
思考1:函数在定义域的某区间上存在满足,且,那么函数一定是增函数吗?
不一定是增函数,如右图
单调性
思考2:函数的单调性是对定义域内某个区间而言的,
(1)你能举出在整个定义域内是单调递增的函数例子吗?
(2)你能举出在定义域内的某些区间单调递增但在另一些区间上单调递减的函数例子吗?
1
2
3
4
5
-1
-2
-3
-4
-2
-3
2
3
o
(1)定义域内是单调递增的函数
(2)某些区间单调递增但在另一些区间上单调递减如右图
Topic. 03
03 函数单调性的证明
证明单调性
判断(证明)单调性:
单调递增
单调递减
证明单调性
1. 根据定义,研究函数 的单调性
解:函数 的定义域是R,对于任意的 且
都有
由 知 ,
这时,函数 是增函数;
当 时, ,即 ,
这时,函数 是减函数;
当 时, ,即 ,
证明单调性
用定义证明函数的单调性的步骤:
1.取数:任取x1,x2∈D,且x1
3.变形:通常是因式分解和配方;
4.定号:判断差f(x1)-f(x2)的正负;
5.结论:指出函数f(x)在给定的区间D上的单调性.
证明单调性
取值
结论
变形
定号
作差
Topic. 04
04 函数单调性应用
求单调区间
1.f(x)的图像如士所示,则函数f(x)的单调递减区间是 ( )
A.(-1,0) B.(1,+∞)
C.(-1,0)∪(1,+∞) D.(-1,0),(1,+∞)
D
求单调区间
2.函数f(x)=x2-2x-3的单调增区间是__________
[变式]函数f(x)=|x2-2x-3|的单调增区间是_____________.
3函数f(x)=-x2+2|x|+1的单调减区间是_______________.
[1,+∞)
[-1,1]和[3,+∞)
[-1,0]和[1,+∞)
求单调区间
求单调区间
求单调区间
增+增=增
减+减=减
增-减=增
减-增=减
注:“增-增”、“减-减”无法确定单调性
求单调区间
4.(多选题)下列函数在 上单调递增的是( ).
A. B. C. D.
CD
应用
应用
Topic. 05
05 课堂小结
课堂小结
总结:
1.函数单调性定义。
2.函数单调性证明
3.函数单调性的应用
NEW
2023/ 07
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
