2023-2024学年人教版七年级数学上册 3.1.2 等式的性质 课件 (共23张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册 3.1.2 等式的性质 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 375.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 22:41:21 | ||
图片预览







文档简介
(共23张PPT)
人教版七年级数学上册课件
教学目标
【知识与技能】
(1)了解等式的概念和等式的两条性质.
(2)学会利用等式的两条性质解简单的一元一次方程.
【过程与方法】
利用天平进行实际操作,培养学生观察、分析、概括及逻辑思维能力,引导学生熟练地运用等式的性质解决问题.
【情感态度与价值观】
渗透“化归”的思想,增强主动探究的意识,发展合理的推理思维.
教学重难点
1.理解和运用等式的性质.
2利用等式的性质把简单的一元一次方程化成“x=a”的形式.
导入新课
问题1:同学们,你们玩过跷跷板吗?它有什么特征?
当跷跷板的两边增加的量之间满足什么关系时,跷跷板能保持平衡?
问题2:用估算的方法我们可以求出简单的一元一次方程的解.你能用这种方法求出方程(1)x-5=22;(2)-0.23+0.17y=1.47的解吗?有没有简单的方法?
问题1学生共同回答,问题2学生小组内交流讨论,教师巡视,指导.
教师:由于问题2中利用估算求方程的解比较困难,今天我们就来学习等式的性质,看它对求方程的解有什么意义.(引入新课,板书课题)
教学过程
一、思考探究,获取新知
1.实验演示.
教师先提出实验的要求:请同学们仔细观察实验的过程,思考能否从中发现规律,再用自己的语言叙述你所发现的规律,然后按如图的方法演示实验.
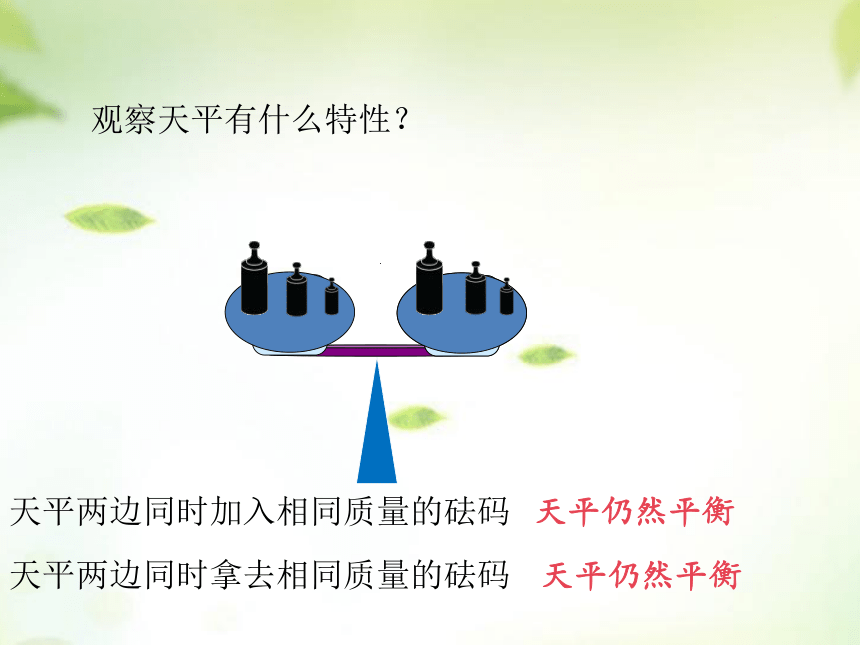
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
提出问题1:你能用文字来叙述等式的这个性质吗?
学生思考,师生共同归纳:
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
+
—
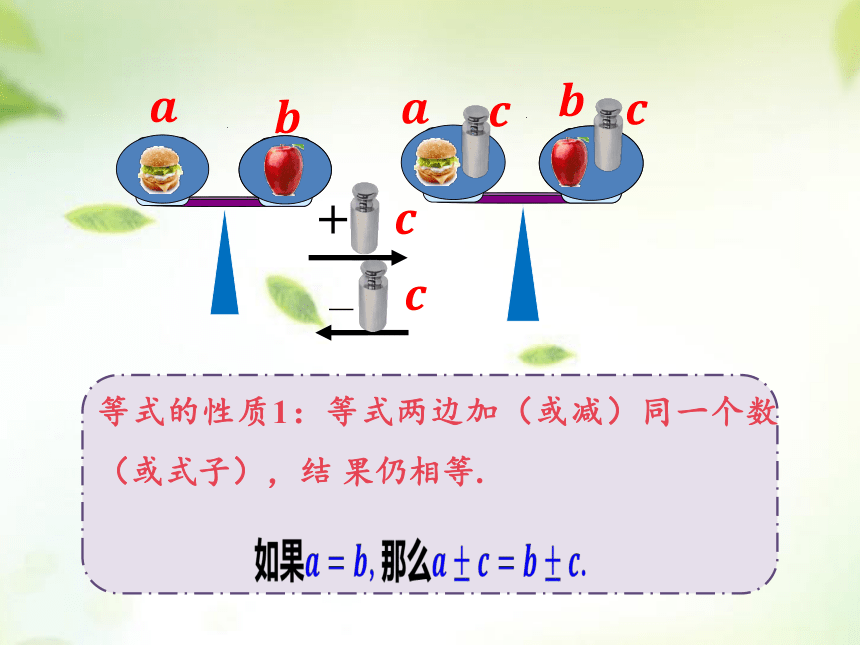
等式的性质1:等式两边加(或减)同一个数(或式子),结 果仍相等.
提出问题2:等式一般可以用a=b来表示,那么等式的性质1用式子的形式怎样来表示?学生思考,师生共同归纳:
如果a=b,那么a±c=b±c.(字母a,b,c可以表示具体的数,也可以表示一个式子.)
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
二、典例精析,掌握新知
例1 利用等式的性质解方程:
(1)0.6-x=2.4;(2)-13x-5=4.
分析:①要把方程0.6-x=2.4转化为x=a的形式,必须去掉方程左边的0.6,怎么去?②要把方程-x=1.8转化为x=a的形式,必须去掉x前面的“-”,怎么去?
小结:
(1)方程的解答中两次运用了等式的性质;(2)解方程的目标是把方程最终化为x=a的形式,运用等式的性质进行变形时,始终要朝着这个目标去转化.
例2服装厂用355米布做成人服装和儿童服装,成人服装每套平均用布3.5米,儿童服装每套平均用布1.5米.现已做了80套成人服装,用余下的布还可以做几套儿童服装?
【解】设余下的布可以做x套儿童服装,那么这x套儿童服装就需要布1.5x米.
根据题意,得80×3.5+1.5x=355.
化简,得280+1.5x=355.
两边同减280,得280+1.5x-280=355-280.
化简,得1.5x=75.
两边同除以1.5,得x=50.
答:用余下的布还可以做50套儿童服装.
教师提出问题:我们如何才能判断所求出的答案50是否正确?
在学生将答案50代入原方程中验算后,教师引导学生归纳出方法:检验一个数是不是某个方程的解,可以把这个数代入方程,看方程的左右两边是否相等.例如,把x=50代入方程80×3.5+1.5x=355的左边,得80×3.5+1.5×50=280+75=355.方程的左右两边相等,所以x=50是方程的解.
课堂小结
1.等式的两个性质是解方程的重要依据,要求学生理解并掌握.
2.用方程解决实际问题时,先设未知数,再根据题意找等量关系,列方程求解,对所求得的解要进行检验
板书设计
课后作业
教材P83习题3.1,第2,4,11题
谢 谢
人教版七年级数学上册课件
教学目标
【知识与技能】
(1)了解等式的概念和等式的两条性质.
(2)学会利用等式的两条性质解简单的一元一次方程.
【过程与方法】
利用天平进行实际操作,培养学生观察、分析、概括及逻辑思维能力,引导学生熟练地运用等式的性质解决问题.
【情感态度与价值观】
渗透“化归”的思想,增强主动探究的意识,发展合理的推理思维.
教学重难点
1.理解和运用等式的性质.
2利用等式的性质把简单的一元一次方程化成“x=a”的形式.
导入新课
问题1:同学们,你们玩过跷跷板吗?它有什么特征?
当跷跷板的两边增加的量之间满足什么关系时,跷跷板能保持平衡?
问题2:用估算的方法我们可以求出简单的一元一次方程的解.你能用这种方法求出方程(1)x-5=22;(2)-0.23+0.17y=1.47的解吗?有没有简单的方法?
问题1学生共同回答,问题2学生小组内交流讨论,教师巡视,指导.
教师:由于问题2中利用估算求方程的解比较困难,今天我们就来学习等式的性质,看它对求方程的解有什么意义.(引入新课,板书课题)
教学过程
一、思考探究,获取新知
1.实验演示.
教师先提出实验的要求:请同学们仔细观察实验的过程,思考能否从中发现规律,再用自己的语言叙述你所发现的规律,然后按如图的方法演示实验.
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
提出问题1:你能用文字来叙述等式的这个性质吗?
学生思考,师生共同归纳:
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
+
—
等式的性质1:等式两边加(或减)同一个数(或式子),结 果仍相等.
提出问题2:等式一般可以用a=b来表示,那么等式的性质1用式子的形式怎样来表示?学生思考,师生共同归纳:
如果a=b,那么a±c=b±c.(字母a,b,c可以表示具体的数,也可以表示一个式子.)
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
二、典例精析,掌握新知
例1 利用等式的性质解方程:
(1)0.6-x=2.4;(2)-13x-5=4.
分析:①要把方程0.6-x=2.4转化为x=a的形式,必须去掉方程左边的0.6,怎么去?②要把方程-x=1.8转化为x=a的形式,必须去掉x前面的“-”,怎么去?
小结:
(1)方程的解答中两次运用了等式的性质;(2)解方程的目标是把方程最终化为x=a的形式,运用等式的性质进行变形时,始终要朝着这个目标去转化.
例2服装厂用355米布做成人服装和儿童服装,成人服装每套平均用布3.5米,儿童服装每套平均用布1.5米.现已做了80套成人服装,用余下的布还可以做几套儿童服装?
【解】设余下的布可以做x套儿童服装,那么这x套儿童服装就需要布1.5x米.
根据题意,得80×3.5+1.5x=355.
化简,得280+1.5x=355.
两边同减280,得280+1.5x-280=355-280.
化简,得1.5x=75.
两边同除以1.5,得x=50.
答:用余下的布还可以做50套儿童服装.
教师提出问题:我们如何才能判断所求出的答案50是否正确?
在学生将答案50代入原方程中验算后,教师引导学生归纳出方法:检验一个数是不是某个方程的解,可以把这个数代入方程,看方程的左右两边是否相等.例如,把x=50代入方程80×3.5+1.5x=355的左边,得80×3.5+1.5×50=280+75=355.方程的左右两边相等,所以x=50是方程的解.
课堂小结
1.等式的两个性质是解方程的重要依据,要求学生理解并掌握.
2.用方程解决实际问题时,先设未知数,再根据题意找等量关系,列方程求解,对所求得的解要进行检验
板书设计
课后作业
教材P83习题3.1,第2,4,11题
谢 谢
