1.5.1乘方(1)[上学期]
文档属性
| 名称 | 1.5.1乘方(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 221.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-23 00:00:00 | ||
图片预览






文档简介
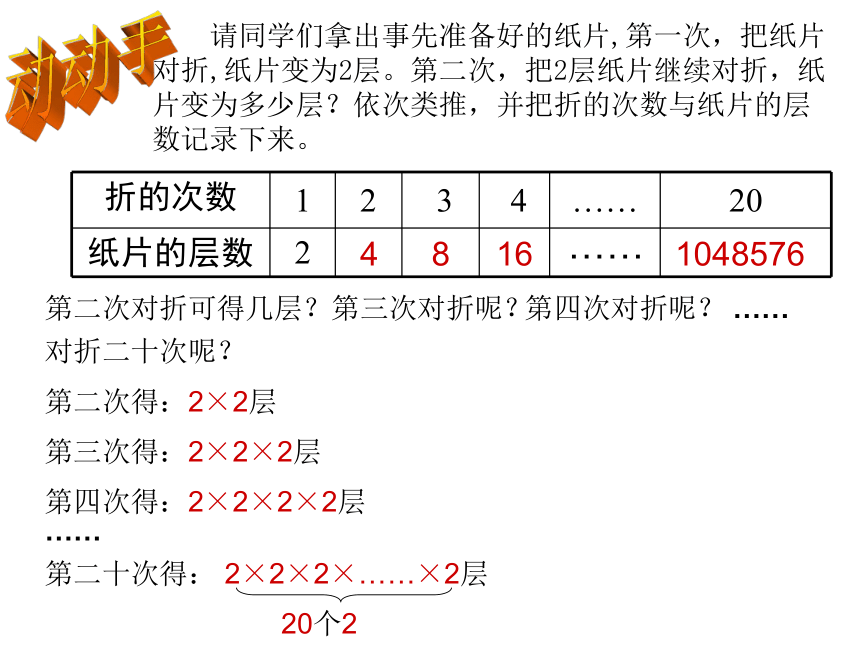
课件20张PPT。有理数的乘方(一) 请同学们拿出事先准备好的纸片,第一次,把纸片 对折,纸片变为2层。第二次,把2层纸片继续对折,纸片变为多少层?依次类推,并把折的次数与纸片的层数记录下来。
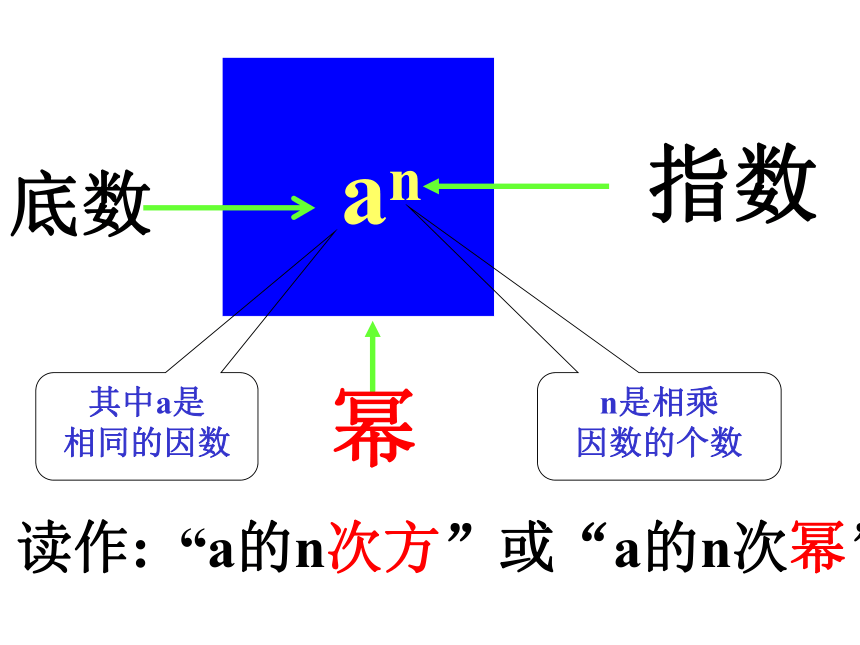
第二次对折可得几层?第三次对折呢?第四次对折呢?对折二十次呢?第二次得:2×2层第三次得:2×2×2层第四次得:2×2×2×2层…………第二十次得: 2×2×2×……×2层20个248161048576……动动手2×22×2×22×2×2×2……请认真观察下面的式子:=22=24=220=23=2100上面算式有什么特点?a×a×a···×an个aan= 一般的,我们把n个相同因数a相乘的积记作:其中a是相同的因数,n是相乘因数的个数.这种求几个相同因数的积的运算叫做乘方,乘方的结果叫幂 读作: “a的n次方”或“a的n次幂”其中a是
相同的因数n是相乘
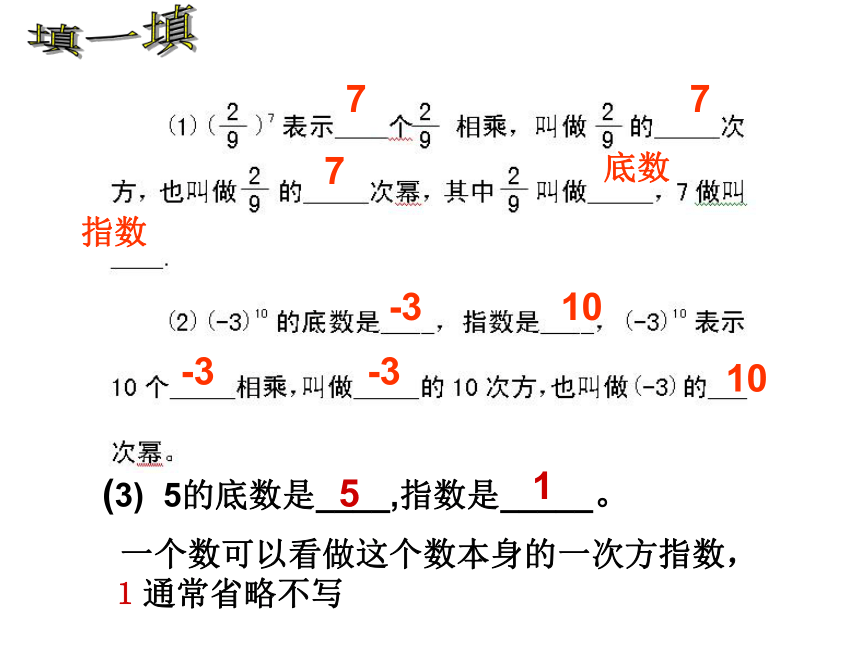
因数的个数请同学们读一下:(1)(-7 ) 、(2)(-2 ) 32读一读(1 ) 读作: -7的2次方或-7的2次幂 还可以读作: -7的平方(2 ) 读作: -2的3次方或-2的3次幂还可以读作: -2的立方777底数指数-310-3-310填一填(3) 5的底数是____,指数是_____。51 一个数可以看做这个数本身的一次方指数,1通常省略不写
2、把(-2)×(-2)×… ×(-2)写成幂的形式:
1、把 写成几个相同因数相乘的形式.
10个(-2)做一做-210= - 2×2×…×210个2(-2)10=3、把下列相同因数的乘积写成幂的形式,并说出底数和指数:
⑴ (-6)×(-6)×(-6)
⑵
幂的底数是负数或分数时,底数应该添上括号
=(-6)3例1计算:(1) (2) (3) (4) (5) 10114320)1(34)5.1()3(-???è?--(1)102=__ __ 103=____ 104=____ 105=____
(2)(-10)2=____ (-10)3=__ __ (-10)4=__ ___(-10)5=__ __
(3)0.12=_____ 0.13=_____ 0.14=_____ 0.15=_____
(4)(-0.1)2=____(-0.1)3=____ (-0.1)4=_____ (-0.1)5=____
100100010000100000100-100010000-1000000.010.0010.00010.000010.01-0.0010.0001-0.00001练一练想一想:观察上述计算结果,你发现了什么规律?
(1)10的几次方,1后面就有几个O。
(2)0.1的几次方,1前面就有几个0。
(3)正数的任何次幂,还是正数。
(4)负数的奇次幂是负数,偶次幂是正数。
算一算:动一动:
用计算器计算: 和解:用带符号键(-)的计算器。( (-) 8 ) ^ 5 =显示:(-8)^5
-32768( (-) 3 ) ^ 6 =显示:(-3)^6
729用带符号转换键 的计算器 +/-+/-^=+/-^=8 53 6 显示: -32768显示:7291048576×0.1=104857.6(毫米)104.8576 ÷ 3≈ 35(层) 连续对折20次,纸片变为1048576层,若对折的纸厚度为0.1毫米,会有多厚?它相当于大概多少层楼高?(若每层楼为3米)算一算你说数学神奇吗?解:104857.6毫米=104.8576米海拔约8848米如果一层楼高按3米计算,把足够长的厚0.1毫米的纸片继续折叠20次,会有几层楼高?35层继续折叠,30次后就有_____个珠穆朗玛峰的高度。 真的很奇妙吧!不可思议的现象:考一考 : 目前已学过几种运算 乘方的概念 乘方运算 乘方运算中的一些规律.收获: “乘方”精神:虽然是简简单单的重复,但结果却是惊人的。学习也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。课后赠言再见
第二次对折可得几层?第三次对折呢?第四次对折呢?对折二十次呢?第二次得:2×2层第三次得:2×2×2层第四次得:2×2×2×2层…………第二十次得: 2×2×2×……×2层20个248161048576……动动手2×22×2×22×2×2×2……请认真观察下面的式子:=22=24=220=23=2100上面算式有什么特点?a×a×a···×an个aan= 一般的,我们把n个相同因数a相乘的积记作:其中a是相同的因数,n是相乘因数的个数.这种求几个相同因数的积的运算叫做乘方,乘方的结果叫幂 读作: “a的n次方”或“a的n次幂”其中a是
相同的因数n是相乘
因数的个数请同学们读一下:(1)(-7 ) 、(2)(-2 ) 32读一读(1 ) 读作: -7的2次方或-7的2次幂 还可以读作: -7的平方(2 ) 读作: -2的3次方或-2的3次幂还可以读作: -2的立方777底数指数-310-3-310填一填(3) 5的底数是____,指数是_____。51 一个数可以看做这个数本身的一次方指数,1通常省略不写
2、把(-2)×(-2)×… ×(-2)写成幂的形式:
1、把 写成几个相同因数相乘的形式.
10个(-2)做一做-210= - 2×2×…×210个2(-2)10=3、把下列相同因数的乘积写成幂的形式,并说出底数和指数:
⑴ (-6)×(-6)×(-6)
⑵
幂的底数是负数或分数时,底数应该添上括号
=(-6)3例1计算:(1) (2) (3) (4) (5) 10114320)1(34)5.1()3(-???è?--(1)102=__ __ 103=____ 104=____ 105=____
(2)(-10)2=____ (-10)3=__ __ (-10)4=__ ___(-10)5=__ __
(3)0.12=_____ 0.13=_____ 0.14=_____ 0.15=_____
(4)(-0.1)2=____(-0.1)3=____ (-0.1)4=_____ (-0.1)5=____
100100010000100000100-100010000-1000000.010.0010.00010.000010.01-0.0010.0001-0.00001练一练想一想:观察上述计算结果,你发现了什么规律?
(1)10的几次方,1后面就有几个O。
(2)0.1的几次方,1前面就有几个0。
(3)正数的任何次幂,还是正数。
(4)负数的奇次幂是负数,偶次幂是正数。
算一算:动一动:
用计算器计算: 和解:用带符号键(-)的计算器。( (-) 8 ) ^ 5 =显示:(-8)^5
-32768( (-) 3 ) ^ 6 =显示:(-3)^6
729用带符号转换键 的计算器 +/-+/-^=+/-^=8 53 6 显示: -32768显示:7291048576×0.1=104857.6(毫米)104.8576 ÷ 3≈ 35(层) 连续对折20次,纸片变为1048576层,若对折的纸厚度为0.1毫米,会有多厚?它相当于大概多少层楼高?(若每层楼为3米)算一算你说数学神奇吗?解:104857.6毫米=104.8576米海拔约8848米如果一层楼高按3米计算,把足够长的厚0.1毫米的纸片继续折叠20次,会有几层楼高?35层继续折叠,30次后就有_____个珠穆朗玛峰的高度。 真的很奇妙吧!不可思议的现象:考一考 : 目前已学过几种运算 乘方的概念 乘方运算 乘方运算中的一些规律.收获: “乘方”精神:虽然是简简单单的重复,但结果却是惊人的。学习也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。课后赠言再见
