8 数学广角——找次品(课件)(共22张PPT)-五年级下册数学 人教版
文档属性
| 名称 | 8 数学广角——找次品(课件)(共22张PPT)-五年级下册数学 人教版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 20:39:12 | ||
图片预览








文档简介
(共22张PPT)
人教版五年级数学下册
8 数学广角——找次品
一、情景导入
二、探究新知
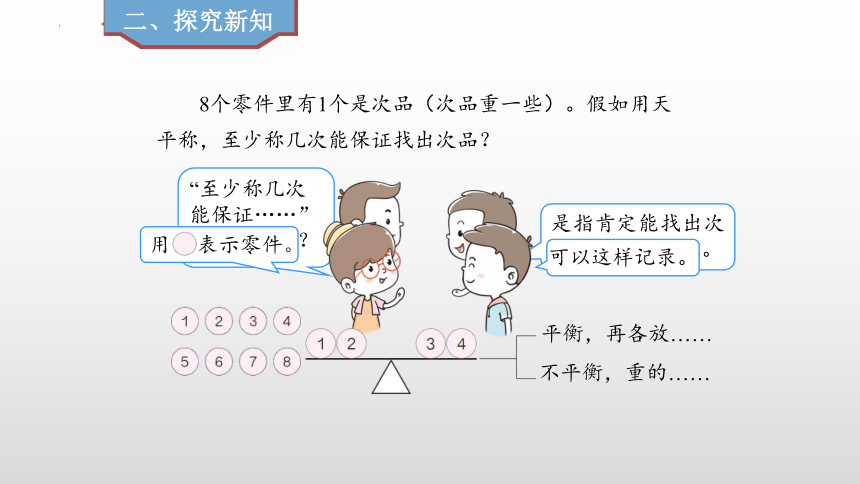
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
“至少称几次能保证……”是什么意思?
是指肯定能找出次品的最少次数吧。
用 表示零件。
可以这样记录。
平衡,再各放……
不平衡,重的……
每次每边放的个数 分成的份数 至少要称的次数
1 8 4
2 4 3
4 2 3
3 3 2
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
二、通过探索,了解稍复杂的找次品问题
至少称3次
平衡,称剩下的2袋,轻的是这袋糖果
不平衡,轻的是这袋糖果
称较轻的一端4袋中的2袋
平衡,称剩下的2袋,轻的是这袋糖果
不平衡,轻的是这袋糖果
称剩下4袋中的2袋
小于或等于 3n 个物体中有一个次品,至少需要称 n 次才能保证找出次品。
规律:
①有20个物品,其中有一个次品(已知次品比正品重或轻),保证能找出次品至少需要称几次?
因为9<20<27,即20<33,所以只要称3次就可以了。
②要保证6次能测出次品,待测物品可能是多少个?
待测物品可能是244个。
运用规律,解决问题
新课讲解
第二次
第三次
我用这种方法要称3次才能保证找到次品
方法三
我把这些零件分成3份;我是这样分的(3,3,2)。
第一次
第二次
第一次
第二次
我用这种方法要称2次才能保证找到次品
新课讲解
9个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次就保证一定能找出次品?
观察完成的表格,你发现了什么?
(1)“分成的份数”、分的方法与找出次品所要称的次数有什么关系?
(2)怎样分找出次品需要称的次数最少?
用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
当堂检测 及时反馈
1.有3盒巧克力,其中的一盒为次品(可能比其他2盒轻,也可能
比其他2盒重),用天平至少称( )次,能保证找出那盒次品。
A.1 B.2 C.3
B
天平左右两边各放一盒巧克力,如果平衡,剩下的为次品;如果不平衡,可取下轻的(或重的),把剩下的那盒放在天平上。若平衡,则取下的为次品;若不平衡,则重的(或轻的)为次品。
分析:
2.为了用尽可能少的次数找出次品,请你对待测物品进行分组。
(每组物品里有1个次品)
待测物品个数 首次分成
6 (2,2,2)
15
19
25
(5,5,5)
(6,6,7)
(8,8,9)
3.有14个球,其中13个质量相同,余下的一个质量较轻,是不合
格产品,用天平至少称几次才能保证找出这个不合格产品?
答:至少称3次能保证找出这个球。
14—(5,5,4)
平衡:
4 —(2,2)
2 —(1,1)
平衡:1
不平衡:2 —(1,1)
不平衡:
5 —(2,2,1)
拓展延伸 能力提升
1.小刚要从12个同一种型号的零件中找出一个质量较轻的次品,
小丽要从27个零件中找出一个质量较重的次品。判断下面的
说法是否正确。(对的画“ ”,错的画“ ”)
(1)小丽用的次数一定比小刚多。 ( )
(2)小丽用的次数一定比小刚少。 ( )
(3)小丽用的次数不一定比小刚多。 ( )
2.有8瓶矿泉水,编号是①至⑧,其中有6瓶一样重,是合格产品,
另外2瓶都轻5g,是不合格产品。用天平称了3次,结果如下:
第一次①+②比③+④重;第二次⑤+⑥比⑦+⑧轻;第三次①+
③+⑤与②+④+⑧一样重。那么这2瓶不合格产品分别是几号?
④+⑤
你知道吗?
用天平找次品时,所测物品数目与至少需要测试的次数有以下关系。(只含一个次品,已知次品比正品重或轻。)
(1)要保证6次能测出
次品,待测物品
可能是多少个?
(2)从左表中你能发现
什么规律?为什么?
要辨别的物品数目 保证能找出次品至少需要测的次数
2~3 1
4~9 2
10~27 3
28~81 4
82~243 5
…… ……
板书设计 思维导图
找次品
每次每边放的个数 分成的份数 至少要称的次数
1
8
4
2
4
3
4
2
3
3
3
2
在找次品时,把物体分成3份,每份数量尽量平均时,可以保证找出次品时称量的次数最少。
1
2
3
4
5
6
7
8
人教版五年级数学下册
8 数学广角——找次品
一、情景导入
二、探究新知
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
“至少称几次能保证……”是什么意思?
是指肯定能找出次品的最少次数吧。
用 表示零件。
可以这样记录。
平衡,再各放……
不平衡,重的……
每次每边放的个数 分成的份数 至少要称的次数
1 8 4
2 4 3
4 2 3
3 3 2
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
二、通过探索,了解稍复杂的找次品问题
至少称3次
平衡,称剩下的2袋,轻的是这袋糖果
不平衡,轻的是这袋糖果
称较轻的一端4袋中的2袋
平衡,称剩下的2袋,轻的是这袋糖果
不平衡,轻的是这袋糖果
称剩下4袋中的2袋
小于或等于 3n 个物体中有一个次品,至少需要称 n 次才能保证找出次品。
规律:
①有20个物品,其中有一个次品(已知次品比正品重或轻),保证能找出次品至少需要称几次?
因为9<20<27,即20<33,所以只要称3次就可以了。
②要保证6次能测出次品,待测物品可能是多少个?
待测物品可能是244个。
运用规律,解决问题
新课讲解
第二次
第三次
我用这种方法要称3次才能保证找到次品
方法三
我把这些零件分成3份;我是这样分的(3,3,2)。
第一次
第二次
第一次
第二次
我用这种方法要称2次才能保证找到次品
新课讲解
9个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次就保证一定能找出次品?
观察完成的表格,你发现了什么?
(1)“分成的份数”、分的方法与找出次品所要称的次数有什么关系?
(2)怎样分找出次品需要称的次数最少?
用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
当堂检测 及时反馈
1.有3盒巧克力,其中的一盒为次品(可能比其他2盒轻,也可能
比其他2盒重),用天平至少称( )次,能保证找出那盒次品。
A.1 B.2 C.3
B
天平左右两边各放一盒巧克力,如果平衡,剩下的为次品;如果不平衡,可取下轻的(或重的),把剩下的那盒放在天平上。若平衡,则取下的为次品;若不平衡,则重的(或轻的)为次品。
分析:
2.为了用尽可能少的次数找出次品,请你对待测物品进行分组。
(每组物品里有1个次品)
待测物品个数 首次分成
6 (2,2,2)
15
19
25
(5,5,5)
(6,6,7)
(8,8,9)
3.有14个球,其中13个质量相同,余下的一个质量较轻,是不合
格产品,用天平至少称几次才能保证找出这个不合格产品?
答:至少称3次能保证找出这个球。
14—(5,5,4)
平衡:
4 —(2,2)
2 —(1,1)
平衡:1
不平衡:2 —(1,1)
不平衡:
5 —(2,2,1)
拓展延伸 能力提升
1.小刚要从12个同一种型号的零件中找出一个质量较轻的次品,
小丽要从27个零件中找出一个质量较重的次品。判断下面的
说法是否正确。(对的画“ ”,错的画“ ”)
(1)小丽用的次数一定比小刚多。 ( )
(2)小丽用的次数一定比小刚少。 ( )
(3)小丽用的次数不一定比小刚多。 ( )
2.有8瓶矿泉水,编号是①至⑧,其中有6瓶一样重,是合格产品,
另外2瓶都轻5g,是不合格产品。用天平称了3次,结果如下:
第一次①+②比③+④重;第二次⑤+⑥比⑦+⑧轻;第三次①+
③+⑤与②+④+⑧一样重。那么这2瓶不合格产品分别是几号?
④+⑤
你知道吗?
用天平找次品时,所测物品数目与至少需要测试的次数有以下关系。(只含一个次品,已知次品比正品重或轻。)
(1)要保证6次能测出
次品,待测物品
可能是多少个?
(2)从左表中你能发现
什么规律?为什么?
要辨别的物品数目 保证能找出次品至少需要测的次数
2~3 1
4~9 2
10~27 3
28~81 4
82~243 5
…… ……
板书设计 思维导图
找次品
每次每边放的个数 分成的份数 至少要称的次数
1
8
4
2
4
3
4
2
3
3
3
2
在找次品时,把物体分成3份,每份数量尽量平均时,可以保证找出次品时称量的次数最少。
1
2
3
4
5
6
7
8
