2023-2024学年人教版七年级数学上册3.2解一元一次方程(一)——合并同类项与移项(2)课件 22张PPT
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册3.2解一元一次方程(一)——合并同类项与移项(2)课件 22张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 868.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 00:00:00 | ||
图片预览







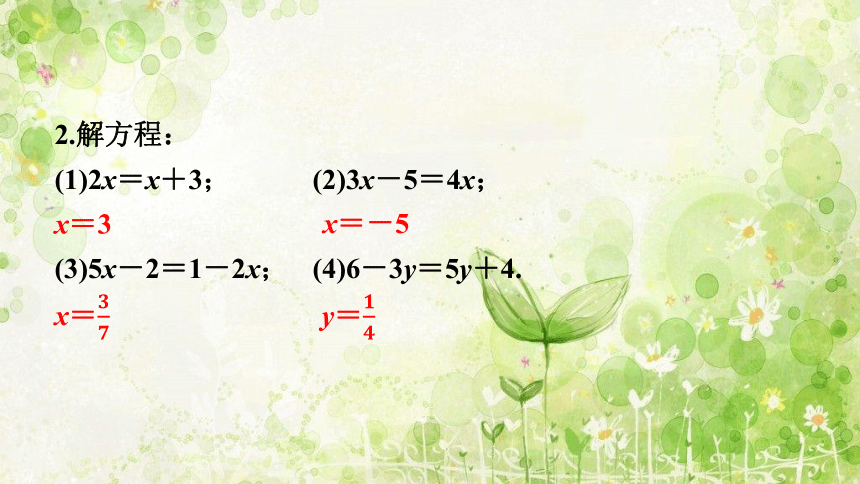

文档简介
(共22张PPT)
第三章 一元一次方程
解一元一次方程(一)
——合并同类项与移项(2)
教学目标:
【知识与技能】
掌握移项的方法,学会解“ax+b=cx+d”形式的一元一次方程,理解解方程的目标,体会解法中蕴含的化归思想.
【过程与方法】
通过方程的简单变形,体会解一元一次方程的基本步骤:“移项”“合并同类项”和“系数化为1”.
【情感态度与价值观】
培养学生积极思考,勇于探索的精神.
教学重难点:
1“移项”和“系数化为1”.
2寻找实际问题中的相等关系,列出方程.
1.知道什么是移项,熟练掌握移项的方法.
2.(2022新课标)能解一元一次方程.(移项)
3.逐步认识数学是解决实际问题和进行交流的重要工具.
知识点一:移项
(1)将等式中的某些项变号后,从等式的一边 另一边的变形叫做移项.
(2)例如:把方程2y-6=y+7变形为2y-y=7+6,这种变形叫移项.根据是 .
(3)注意:移项前等式的两边的项数与移项后等式的两边的项数不变.
等式的性质1
移到
1.用适当的数或式子填空,使所得的结果仍是等式.
(1)如果2x+7=10,那么2x=10- ;
(2)如果5x=4x+7,那么5x- =7;
(3)如果x-3=2,那么x=2+ .
3
4x
7
知识点二:用移项法解一元一次方程
(1)移项的目的是把所有 移到方程的一边,把所有 移到方程的另一边.
(2)一般地,把未知项移到方程的左边,常数项移到方程的右边,这样就可以通过“合并”把方程转化为x=a的形式.
(3)解方程时经常要“合并同类项”和“移项”,前面提到的古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”.
常数项
未知项
2.解方程:
(1)2x=x+3; (2)3x-5=4x;
x=3
(3)5x-2=1-2x; (4)6-3y=5y+4.
x=-5
x=
y=
知识点三:列方程解用不同的式子表示同一个量的问题
(1)注意变化中的不变量,寻找隐含的相等关系.
(2)(人教7上P88)例如:把一些图书分给某班x名学生阅读.
如果每人分3本,那么剩余20本.
分析:每人分3本,共分出3x本,加上剩余的20本,这批书共( )本.
如果每人分4本,那么还缺25本.
3x+20
分析:每人分4本,需要4x本,减去缺的25本,这批书共( )本.
这批书的总数是一个定值,表示它的两个式子应相等,根据相等关系列方程为 .
总结:表示同一个量的两个不同式子 .
相等
3x+20=4x-25
4x-25
3.(跨学科融合)(2022西安四模)冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,体现了追求卓越、引领时代,以及面向未来的无限可能.某学校购进了一批冰墩墩吉祥物分配给各班,若每班分4个,则剩余2个;若每班分5个,则还缺16个.求这个学校有几个班级.
解:设这个学校有x个班级,
依题意得4x+2=5x-16,解得x=18.
答:这个学校有18个班级.
4.【例1】下面的移项对不对?
(1)由7+x=13得x=13+7;( )
(2)由5x=4x+8得5x-4x=8;( )
(3)由3x-2=x+1得3x+x=2+1;( )
(4)由8x=7x-2得8x-7x=2.( )
不对
不对
对
不对
小结:移项要改变符号,不移动的项不改变符号.
5.【例2】解方程:
(1)6x+2=5x; (2)2t-5=8t+15;
x=-2
(3)-2y=; (4)4-m=-m.
t=-
y=-
m=6
小结:解等号两边都有未知数的一元一次方程时,一般先移项,再合并同类项,最后把未知数的系数化为1.
6.【例3】今年黄金周的第一天,某网店销售收入为 28 000元,比去年同期的2倍还多500元,去年同一天该网店销售收入多少元?
解:设去年同一天该网店销售收入x元,
由题意,得2x+500=28 000,
2x=27 500,∴x=13 750.
答:去年同一天该网店销售收入13 750元.
小结:关键在于找出未知量与已知量的关系.即“去年同期(未知量)×2+500元=今年同期28 000元(已知量)”.
7.【例4】一个长方形和一个正方形,长方形的长比正方形的边长多4 cm,长方形的宽比正方形的边长少2 cm,长方形的长、宽之比为5∶3,长方形的长、宽各是多少?
解:设长方形的长、宽分别为5x cm,3x cm,
由题意,得5x-4=3x+2,∴x=3.∴5x=15,3x=9.
答:长方形的长、宽分别为15 cm,9 cm.
小结:按长、宽之比分别表示出长方形的长为5x,宽为3x,再分别表示出正方形的边长的两个不同式子,列等式.
8.下列式子的变形,属于移项的是( )
A.由2x-2y-1得-1-2y+2x
B.由6x-1=x+5得6x-1=5+x
C.由4-x=3x-2得3x-2=4-x
D.由2+x=-2x-2得x+2x=-2-2
D
9.解方程:
(1)2x-3=5x; (2)4x=5x-2;
x=-1
(3)0.3x+1.2-2x=1.2-2.7x;
x=0
(4)40×10%x-5=100×20%+12x.
x=2
x=-
10.有两个仓库,A仓库存货30吨,B仓库存货50吨.A仓库每天入货2吨,B仓库每天出货3吨.几天后两个仓库存货量相等?
解:设x天后两个仓库存货量相等,
由题意,得30+2x=50-3x,∴x=4.
答:4天后两个仓库存货量相等.
★11.一个三角形三条边长的比为3∶4∶5,最长边比最短边长4 cm,三角形的周长为多少?
解:设三条边长分别为3x cm,4x cm,5x cm,
由题意,得5x-3x=4,∴x=2,
∴三角形的周长为3x+4x+5x=24(cm).
答:三角形的周长为24 cm.
课堂小结:
移项解一元一次方程就是对方程进行适当的变形,使之转化为x=a的形式;移项要改变符号,且从方程的一边移到另一边;将未知数的系数化为1时要注意系数的符号;解方程时,往往既需要移项,又需要合并同类项.
教材P91习题3.2第2,4,5题
第三章 一元一次方程
解一元一次方程(一)
——合并同类项与移项(2)
教学目标:
【知识与技能】
掌握移项的方法,学会解“ax+b=cx+d”形式的一元一次方程,理解解方程的目标,体会解法中蕴含的化归思想.
【过程与方法】
通过方程的简单变形,体会解一元一次方程的基本步骤:“移项”“合并同类项”和“系数化为1”.
【情感态度与价值观】
培养学生积极思考,勇于探索的精神.
教学重难点:
1“移项”和“系数化为1”.
2寻找实际问题中的相等关系,列出方程.
1.知道什么是移项,熟练掌握移项的方法.
2.(2022新课标)能解一元一次方程.(移项)
3.逐步认识数学是解决实际问题和进行交流的重要工具.
知识点一:移项
(1)将等式中的某些项变号后,从等式的一边 另一边的变形叫做移项.
(2)例如:把方程2y-6=y+7变形为2y-y=7+6,这种变形叫移项.根据是 .
(3)注意:移项前等式的两边的项数与移项后等式的两边的项数不变.
等式的性质1
移到
1.用适当的数或式子填空,使所得的结果仍是等式.
(1)如果2x+7=10,那么2x=10- ;
(2)如果5x=4x+7,那么5x- =7;
(3)如果x-3=2,那么x=2+ .
3
4x
7
知识点二:用移项法解一元一次方程
(1)移项的目的是把所有 移到方程的一边,把所有 移到方程的另一边.
(2)一般地,把未知项移到方程的左边,常数项移到方程的右边,这样就可以通过“合并”把方程转化为x=a的形式.
(3)解方程时经常要“合并同类项”和“移项”,前面提到的古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”.
常数项
未知项
2.解方程:
(1)2x=x+3; (2)3x-5=4x;
x=3
(3)5x-2=1-2x; (4)6-3y=5y+4.
x=-5
x=
y=
知识点三:列方程解用不同的式子表示同一个量的问题
(1)注意变化中的不变量,寻找隐含的相等关系.
(2)(人教7上P88)例如:把一些图书分给某班x名学生阅读.
如果每人分3本,那么剩余20本.
分析:每人分3本,共分出3x本,加上剩余的20本,这批书共( )本.
如果每人分4本,那么还缺25本.
3x+20
分析:每人分4本,需要4x本,减去缺的25本,这批书共( )本.
这批书的总数是一个定值,表示它的两个式子应相等,根据相等关系列方程为 .
总结:表示同一个量的两个不同式子 .
相等
3x+20=4x-25
4x-25
3.(跨学科融合)(2022西安四模)冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,体现了追求卓越、引领时代,以及面向未来的无限可能.某学校购进了一批冰墩墩吉祥物分配给各班,若每班分4个,则剩余2个;若每班分5个,则还缺16个.求这个学校有几个班级.
解:设这个学校有x个班级,
依题意得4x+2=5x-16,解得x=18.
答:这个学校有18个班级.
4.【例1】下面的移项对不对?
(1)由7+x=13得x=13+7;( )
(2)由5x=4x+8得5x-4x=8;( )
(3)由3x-2=x+1得3x+x=2+1;( )
(4)由8x=7x-2得8x-7x=2.( )
不对
不对
对
不对
小结:移项要改变符号,不移动的项不改变符号.
5.【例2】解方程:
(1)6x+2=5x; (2)2t-5=8t+15;
x=-2
(3)-2y=; (4)4-m=-m.
t=-
y=-
m=6
小结:解等号两边都有未知数的一元一次方程时,一般先移项,再合并同类项,最后把未知数的系数化为1.
6.【例3】今年黄金周的第一天,某网店销售收入为 28 000元,比去年同期的2倍还多500元,去年同一天该网店销售收入多少元?
解:设去年同一天该网店销售收入x元,
由题意,得2x+500=28 000,
2x=27 500,∴x=13 750.
答:去年同一天该网店销售收入13 750元.
小结:关键在于找出未知量与已知量的关系.即“去年同期(未知量)×2+500元=今年同期28 000元(已知量)”.
7.【例4】一个长方形和一个正方形,长方形的长比正方形的边长多4 cm,长方形的宽比正方形的边长少2 cm,长方形的长、宽之比为5∶3,长方形的长、宽各是多少?
解:设长方形的长、宽分别为5x cm,3x cm,
由题意,得5x-4=3x+2,∴x=3.∴5x=15,3x=9.
答:长方形的长、宽分别为15 cm,9 cm.
小结:按长、宽之比分别表示出长方形的长为5x,宽为3x,再分别表示出正方形的边长的两个不同式子,列等式.
8.下列式子的变形,属于移项的是( )
A.由2x-2y-1得-1-2y+2x
B.由6x-1=x+5得6x-1=5+x
C.由4-x=3x-2得3x-2=4-x
D.由2+x=-2x-2得x+2x=-2-2
D
9.解方程:
(1)2x-3=5x; (2)4x=5x-2;
x=-1
(3)0.3x+1.2-2x=1.2-2.7x;
x=0
(4)40×10%x-5=100×20%+12x.
x=2
x=-
10.有两个仓库,A仓库存货30吨,B仓库存货50吨.A仓库每天入货2吨,B仓库每天出货3吨.几天后两个仓库存货量相等?
解:设x天后两个仓库存货量相等,
由题意,得30+2x=50-3x,∴x=4.
答:4天后两个仓库存货量相等.
★11.一个三角形三条边长的比为3∶4∶5,最长边比最短边长4 cm,三角形的周长为多少?
解:设三条边长分别为3x cm,4x cm,5x cm,
由题意,得5x-3x=4,∴x=2,
∴三角形的周长为3x+4x+5x=24(cm).
答:三角形的周长为24 cm.
课堂小结:
移项解一元一次方程就是对方程进行适当的变形,使之转化为x=a的形式;移项要改变符号,且从方程的一边移到另一边;将未知数的系数化为1时要注意系数的符号;解方程时,往往既需要移项,又需要合并同类项.
教材P91习题3.2第2,4,5题
