【同步辅导】2015高中数学北师大版必修五《数列的函数特性》 课件+导学案(2份)
文档属性
| 名称 | 【同步辅导】2015高中数学北师大版必修五《数列的函数特性》 课件+导学案(2份) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-05 16:45:57 | ||
图片预览


文档简介
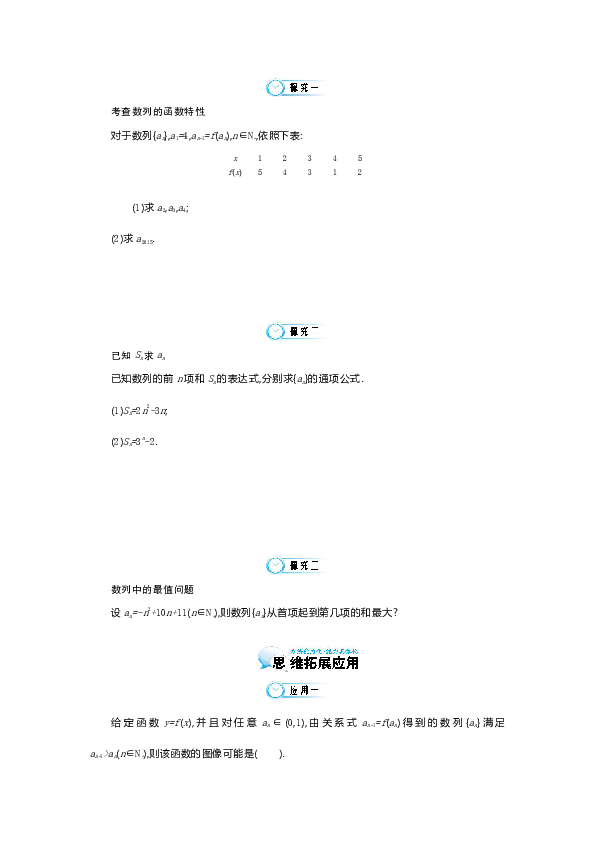
第2课时 数列的函数特性
1.了解数列和函数之间的关系,能用函数的观点研究数列.
2.能判断数列的单调性,并应用单调性求最大(小)项.
3.会由数列的前n项和公式求出其通项公式.
写出数列0,2,4,6,8,…的通项公式an=2n-2后,发现an=2n-2与一次函数f(x)=2x-2有相似之处,只不过是自变量从x换到了n,数列也可看成一种函数.
问题1:数列可以看作是一个定义域为 (或它的有限子集{1,2,3,…,n})的函数,当自变量按照从小到大的顺序依次取值时,对应的一列 .?
问题2:如果数列{an}的第1项或前几项已知,并且数列{an}的任一项an与它的前一项an-1(或前几项)间的关系可以用一个式子来表示,那么这个式子就叫作这个数列的 ,一般记作为 .?
问题3:一般地,一个数列{an},如果从 起,每一项都大于它的前一项,即 ,那么这个数列叫作递增数列.如果从 起,每一项都小于它的前一项,即 ,那么这个数列叫作递减数列.如果数列{an}的各项 ,那么这个数列叫作常数列.?
问题4:任意数列{an}的前n项和Sn的性质
若Sn=a1+a2+a3+…+an,则an= .?
1.下面四个结论:
①数列可以看作是一个定义域在正整数集N+(或它的有限子集{1,2,3,…,n})上的函数;
②数列若用图像表示,从图像上看都是一群孤立的点;
③数列的项数是无限的;
④数列通项的表示式是唯一的.其中正确的是( ).
A.①② B.①②③ C.②③ D.①②③④
2.数列{an}的通项公式为an=3n2-28n,则数列{an}各项中最小项是( ).
A.第4项 B.第5项 C.第6项 D.第7项
3.在某报《自测健康状况》的报道中,自测血压结果与相应年龄的统计数据如下表. 观察表中数据的特点,用适当的数填入表中空白( )内.?
年龄(岁)
30
35
40
45
50
55
60
65
收缩压(水银柱/毫米)
110
115
120
125
130
135
( )?
145
舒张压(水银柱/毫米)
70
73
75
78
80
83
( )?
88
4.数列{an}中,已知an=2n+1-3.
(1)写出a3,a4;
(2)253是否是数列的项?如果是,是第几项?
考查数列的函数特性
对于数列{an},a1=4,an+1=f(an),n∈N+,依照下表:
x
1
2
3
4
5
f(x)
5
4
3
1
2
(1)求a2,a3,a4;
(2)求a2015.
已知Sn求an
已知数列的前n项和Sn的表达式,分别求{an}的通项公式.
(1)Sn=2n2-3n;
(2)Sn=3n-2.
数列中的最值问题
设an=-n2+10n+11(n∈N+),则数列{an}从首项起到第几项的和最大?
给定函数y=f(x),并且对任意an∈(0,1),由关系式an+1=f(an)得到的数列{an}满足an+1>an(n∈N+),则该函数的图像可能是( ).
已知数列{an}的前n项和Sn=3n-2n2 (n∈N+).
(1)求数列{an}的通项公式;
(2)当n≥2时,比较Sn,na1,nan的大小.
已知数列{an}的通项公式an=(n+1)()n(n∈N+),试问数列{an}有没有最大项?若有,求最大项和最大项的项数;若无,说明理由.
1.已知an+1-an-3=0,则数列{an}是( ).
A.递增数列 B.递减数列 C.常数列 D.不能确定
2.已知数列{an}的图像在函数y=的图像上,当x取正整数时,则其通项公式为( ).
A.an=(x∈R) B.an=(n∈N+)
C.an=(x∈N) D.an=(n∈N)
3.已知数列{an}的前n项和为Sn,a1=2,an+1=Sn+1,n∈N+,则a6= .?
4.已知数列{an}中,an=(n∈N+),求数列{an}的最大项.
(2013年·陕西卷)观察下列等式
(1+1)=2×1
(2+1)(2+2)=22×1×3
(3+1)(3+2)(3+3)=23×1×3×5
……
照此规律,第n个等式可为 .?
考题变式(我来改编):
第2课时 数列的函数特性
知识体系梳理
问题1:正整数集N+ 函数值
问题2:递推公式 an=f(an-1)(n≥2)
问题3:第2项 an+1>an 第2项 an+1问题4:
基础学习交流
1.A 由数列的概念及数列的函数特性知,①②正确,故应选A.
2.B 由an=3n2-28n知通项公式是一个二次函数,对称轴是-=-==4,5离4最近,∴最小项是第5项.
3.140 85 观察上表规律,收缩压每次增加5,舒张压相应增加3或2,且是间隔出现的,故应填140,85.
4.解:(1)a3=13,a4=29.
(2)令2n+1-3=253,则2n+1=256,
∴n+1=8,∴n=7,∴253是第7项.
重点难点探究
探究一:【解析】(1)a1=4,a2=f(4)=1,a3=f(1)=5,a4=f(5)=2.
(2)由(1)知a1=4,a2=1,a3=5,a4=2,a5=f(2)=4,…,该数列是周期为4的周期数列,所以a2015=a3=5.
【小结】通过求数列的前几项,发现规律,找到周期是本题的关键.
探究二:【解析】(1)a1=S1=-1,当n≥2时,an=Sn-Sn-1=4n-5,
由于a1也适合此等式,所以an=4n-5.
(2)a1=S1=1,当n≥2时,an=Sn-Sn-1=2·3n-1,
由于a1不适合此等式,
所以an=
【小结】利用an=Sn-Sn-1(n≥2)来求an的方法也可以叫作公式法.
探究三:【解析】an=-n2+10n+11=-(n-5)2+36,
∴当n=5时an最大,∴从首项起到第5项的和最大.
[问题]an最大是从首项起到第n项的和Sn最大吗?
[结论]由于审题不清,错把-n2+10n+11当成Sn,从而利用二次函数知识得到:n=5时,取最大值显然不合题意.
于是,正确解答为:由an=-n2+10n+11≥0得n2-10n-11≤0,∴-1≤n≤11.
即a1,a2,…,a10>0,a11=0,当n≥12时,an<0.
∴从首项起到第10项或第11项的和最大.
【小结】这是一道易错题,审题要清楚,深刻理解通项公式an是关于n(n∈N+)的函数.
思维拓展应用
应用一:A 由?f(an)>an,此式说明了对于函数y=f(x)图像上的任一点,(an,f(an))都有纵坐标f(an)大于横坐标an,所以函数f(x)的图像在直线y=x的上方.
应用二:(1)由an=
解得an=5-4n.
(2)∵a1=5-4×1=1,∴na1=n,
∴nan=5n-4n2,
∴na1-Sn=n-(3n-2n2)=2n2-2n=2n(n-1)>0.
又∵Sn-nan=3n-2n2-(5n-4n2)=2n2-2n>0,
∴na1>Sn>nan.
应用三:(法一:作差法)∵an+1-an=(n+2)()n+1-(n+1)()n=()n,
当n<9时,an+1-an>0,an+1>an;
当n=9时,an+1-an=0,an+1=an;
当n>9时,an+1-an<0,an+1故a1a11>…
∴数列{an}有最大项,为第9,10项.
(法二:作商法)∵==,
当n<9时,10n+20>11n+11,>1,即an+1>an;
当n=9时,10n+20=11n+11,=1,即an+1=an;
当n>9时,10n+20<11n+11,<1,即an+1故a1a11>…
∴数列{an}有最大项,为第9,10项.
(法三:两边夹)假设an为最大项,则
即解得
∴9≤n≤10,∴n=9或10,即第9,10项最大.
基础智能检测
1.A ∵an+1=an+3,∴数列{an}是递增数列.
2.B 数列{an}对应的点列为(n,an),即有an=(n∈N+).
3.48 当n≥2时,an+1=Sn+1,an=Sn-1+1,两式相减,得an+1-an=Sn-Sn-1=an,即an+1=2an,则a2=a1+1=3,a3=2a2=6,a4=2a3=12,a5=2a4=24,a6=2a5=48.
4.解:考察函数y==1+,因为直线x=15.6为函数图像的渐近线,且函数在(-∞,15.6)上单调递减,在(15.6,+∞)上单调递减,所以当n=16时,an最大,即第16项最大.
全新视角拓展
(n+1)(n+2)(n+3)…(n+n)=2n×1×3×…×(2n-1)
根据等式两边的规律可知: 第n个等式为(n+1)(n+2)·(n+3)…(n+n)=2n×1×3×…×(2n-1).
思维导图构建
an=
1.了解数列和函数之间的关系,能用函数的观点研究数列.
2.能判断数列的单调性,并应用单调性求最大(小)项.
3.会由数列的前n项和公式求出其通项公式.
写出数列0,2,4,6,8,…的通项公式an=2n-2后,发现an=2n-2与一次函数f(x)=2x-2有相似之处,只不过是自变量从x换到了n,数列也可看成一种函数.
问题1:数列可以看作是一个定义域为 (或它的有限子集{1,2,3,…,n})的函数,当自变量按照从小到大的顺序依次取值时,对应的一列 .?
问题2:如果数列{an}的第1项或前几项已知,并且数列{an}的任一项an与它的前一项an-1(或前几项)间的关系可以用一个式子来表示,那么这个式子就叫作这个数列的 ,一般记作为 .?
问题3:一般地,一个数列{an},如果从 起,每一项都大于它的前一项,即 ,那么这个数列叫作递增数列.如果从 起,每一项都小于它的前一项,即 ,那么这个数列叫作递减数列.如果数列{an}的各项 ,那么这个数列叫作常数列.?
问题4:任意数列{an}的前n项和Sn的性质
若Sn=a1+a2+a3+…+an,则an= .?
1.下面四个结论:
①数列可以看作是一个定义域在正整数集N+(或它的有限子集{1,2,3,…,n})上的函数;
②数列若用图像表示,从图像上看都是一群孤立的点;
③数列的项数是无限的;
④数列通项的表示式是唯一的.其中正确的是( ).
A.①② B.①②③ C.②③ D.①②③④
2.数列{an}的通项公式为an=3n2-28n,则数列{an}各项中最小项是( ).
A.第4项 B.第5项 C.第6项 D.第7项
3.在某报《自测健康状况》的报道中,自测血压结果与相应年龄的统计数据如下表. 观察表中数据的特点,用适当的数填入表中空白( )内.?
年龄(岁)
30
35
40
45
50
55
60
65
收缩压(水银柱/毫米)
110
115
120
125
130
135
( )?
145
舒张压(水银柱/毫米)
70
73
75
78
80
83
( )?
88
4.数列{an}中,已知an=2n+1-3.
(1)写出a3,a4;
(2)253是否是数列的项?如果是,是第几项?
考查数列的函数特性
对于数列{an},a1=4,an+1=f(an),n∈N+,依照下表:
x
1
2
3
4
5
f(x)
5
4
3
1
2
(1)求a2,a3,a4;
(2)求a2015.
已知Sn求an
已知数列的前n项和Sn的表达式,分别求{an}的通项公式.
(1)Sn=2n2-3n;
(2)Sn=3n-2.
数列中的最值问题
设an=-n2+10n+11(n∈N+),则数列{an}从首项起到第几项的和最大?
给定函数y=f(x),并且对任意an∈(0,1),由关系式an+1=f(an)得到的数列{an}满足an+1>an(n∈N+),则该函数的图像可能是( ).
已知数列{an}的前n项和Sn=3n-2n2 (n∈N+).
(1)求数列{an}的通项公式;
(2)当n≥2时,比较Sn,na1,nan的大小.
已知数列{an}的通项公式an=(n+1)()n(n∈N+),试问数列{an}有没有最大项?若有,求最大项和最大项的项数;若无,说明理由.
1.已知an+1-an-3=0,则数列{an}是( ).
A.递增数列 B.递减数列 C.常数列 D.不能确定
2.已知数列{an}的图像在函数y=的图像上,当x取正整数时,则其通项公式为( ).
A.an=(x∈R) B.an=(n∈N+)
C.an=(x∈N) D.an=(n∈N)
3.已知数列{an}的前n项和为Sn,a1=2,an+1=Sn+1,n∈N+,则a6= .?
4.已知数列{an}中,an=(n∈N+),求数列{an}的最大项.
(2013年·陕西卷)观察下列等式
(1+1)=2×1
(2+1)(2+2)=22×1×3
(3+1)(3+2)(3+3)=23×1×3×5
……
照此规律,第n个等式可为 .?
考题变式(我来改编):
第2课时 数列的函数特性
知识体系梳理
问题1:正整数集N+ 函数值
问题2:递推公式 an=f(an-1)(n≥2)
问题3:第2项 an+1>an 第2项 an+1
基础学习交流
1.A 由数列的概念及数列的函数特性知,①②正确,故应选A.
2.B 由an=3n2-28n知通项公式是一个二次函数,对称轴是-=-==4,5离4最近,∴最小项是第5项.
3.140 85 观察上表规律,收缩压每次增加5,舒张压相应增加3或2,且是间隔出现的,故应填140,85.
4.解:(1)a3=13,a4=29.
(2)令2n+1-3=253,则2n+1=256,
∴n+1=8,∴n=7,∴253是第7项.
重点难点探究
探究一:【解析】(1)a1=4,a2=f(4)=1,a3=f(1)=5,a4=f(5)=2.
(2)由(1)知a1=4,a2=1,a3=5,a4=2,a5=f(2)=4,…,该数列是周期为4的周期数列,所以a2015=a3=5.
【小结】通过求数列的前几项,发现规律,找到周期是本题的关键.
探究二:【解析】(1)a1=S1=-1,当n≥2时,an=Sn-Sn-1=4n-5,
由于a1也适合此等式,所以an=4n-5.
(2)a1=S1=1,当n≥2时,an=Sn-Sn-1=2·3n-1,
由于a1不适合此等式,
所以an=
【小结】利用an=Sn-Sn-1(n≥2)来求an的方法也可以叫作公式法.
探究三:【解析】an=-n2+10n+11=-(n-5)2+36,
∴当n=5时an最大,∴从首项起到第5项的和最大.
[问题]an最大是从首项起到第n项的和Sn最大吗?
[结论]由于审题不清,错把-n2+10n+11当成Sn,从而利用二次函数知识得到:n=5时,取最大值显然不合题意.
于是,正确解答为:由an=-n2+10n+11≥0得n2-10n-11≤0,∴-1≤n≤11.
即a1,a2,…,a10>0,a11=0,当n≥12时,an<0.
∴从首项起到第10项或第11项的和最大.
【小结】这是一道易错题,审题要清楚,深刻理解通项公式an是关于n(n∈N+)的函数.
思维拓展应用
应用一:A 由?f(an)>an,此式说明了对于函数y=f(x)图像上的任一点,(an,f(an))都有纵坐标f(an)大于横坐标an,所以函数f(x)的图像在直线y=x的上方.
应用二:(1)由an=
解得an=5-4n.
(2)∵a1=5-4×1=1,∴na1=n,
∴nan=5n-4n2,
∴na1-Sn=n-(3n-2n2)=2n2-2n=2n(n-1)>0.
又∵Sn-nan=3n-2n2-(5n-4n2)=2n2-2n>0,
∴na1>Sn>nan.
应用三:(法一:作差法)∵an+1-an=(n+2)()n+1-(n+1)()n=()n,
当n<9时,an+1-an>0,an+1>an;
当n=9时,an+1-an=0,an+1=an;
当n>9时,an+1-an<0,an+1
∴数列{an}有最大项,为第9,10项.
(法二:作商法)∵==,
当n<9时,10n+20>11n+11,>1,即an+1>an;
当n=9时,10n+20=11n+11,=1,即an+1=an;
当n>9时,10n+20<11n+11,<1,即an+1
∴数列{an}有最大项,为第9,10项.
(法三:两边夹)假设an为最大项,则
即解得
∴9≤n≤10,∴n=9或10,即第9,10项最大.
基础智能检测
1.A ∵an+1=an+3,∴数列{an}是递增数列.
2.B 数列{an}对应的点列为(n,an),即有an=(n∈N+).
3.48 当n≥2时,an+1=Sn+1,an=Sn-1+1,两式相减,得an+1-an=Sn-Sn-1=an,即an+1=2an,则a2=a1+1=3,a3=2a2=6,a4=2a3=12,a5=2a4=24,a6=2a5=48.
4.解:考察函数y==1+,因为直线x=15.6为函数图像的渐近线,且函数在(-∞,15.6)上单调递减,在(15.6,+∞)上单调递减,所以当n=16时,an最大,即第16项最大.
全新视角拓展
(n+1)(n+2)(n+3)…(n+n)=2n×1×3×…×(2n-1)
根据等式两边的规律可知: 第n个等式为(n+1)(n+2)·(n+3)…(n+n)=2n×1×3×…×(2n-1).
思维导图构建
an=
