北师大版数学四年级上册2.4旋转与角课后训练(含解析)
文档属性
| 名称 | 北师大版数学四年级上册2.4旋转与角课后训练(含解析) | 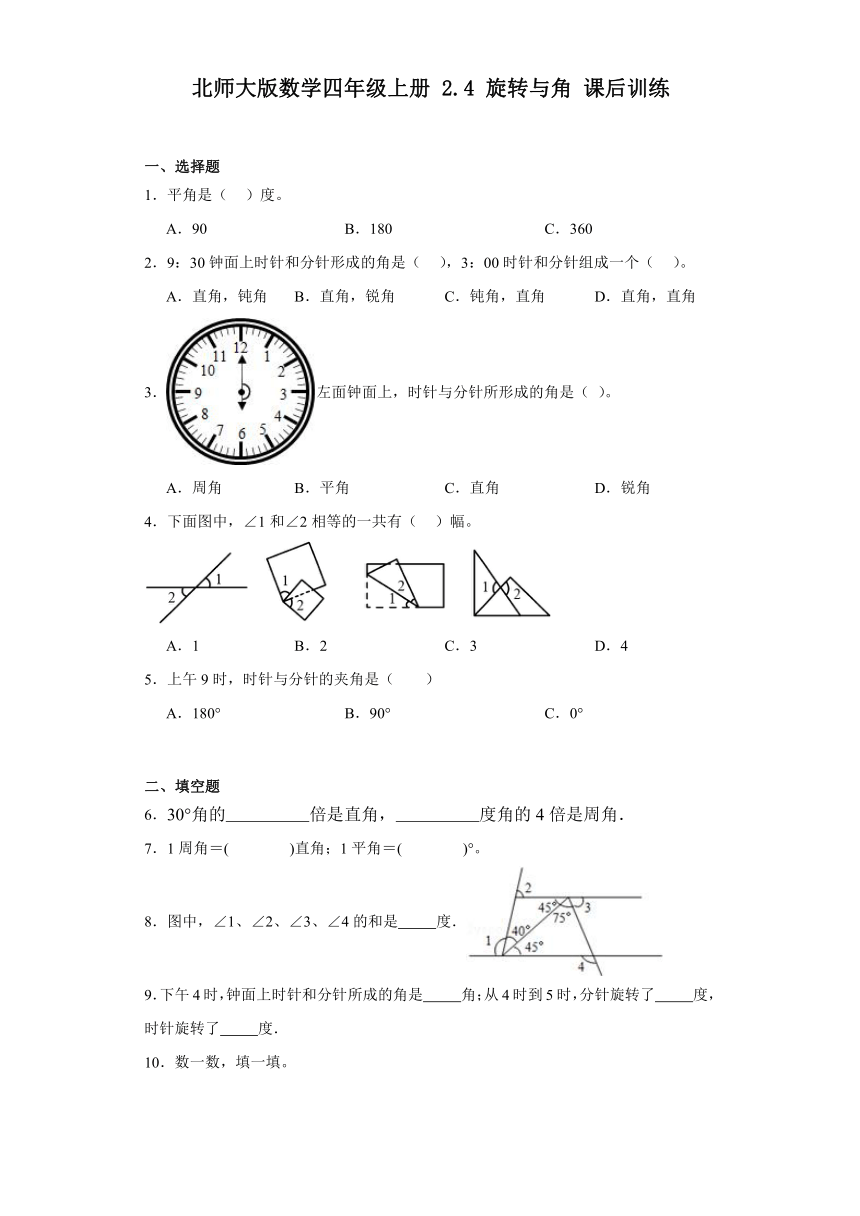 | |
| 格式 | docx | ||
| 文件大小 | 104.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-23 22:18:44 | ||
图片预览





文档简介
北师大版数学四年级上册 2.4 旋转与角 课后训练
一、选择题
1.平角是( )度。
A.90 B.180 C.360
2.9:30钟面上时针和分针形成的角是( ),3:00时针和分针组成一个( )。
A.直角,钝角 B.直角,锐角 C.钝角,直角 D.直角,直角
3.左面钟面上,时针与分针所形成的角是( )。
A.周角 B.平角 C.直角 D.锐角
4.下面图中,∠1和∠2相等的一共有( )幅。
A.1 B.2 C.3 D.4
5.上午9时,时针与分针的夹角是( )
A.180° B.90° C.0°
二、填空题
6.30°角的 倍是直角, 度角的4倍是周角.
7.1周角=( )直角;1平角=( )°。
8.图中,∠1、∠2、∠3、∠4的和是 度.
9.下午4时,钟面上时针和分针所成的角是 角;从4时到5时,分针旋转了 度,时针旋转了 度.
10.数一数,填一填。
有( )个角。
三、判断题
11.用放大10倍的放大镜看的角,看到的角的度数是。( )
12.1周角=4平角。( )
13.小于90°的角叫做直角. ( )
14.把角的两条边延长2倍,角的大小不变。( )
15.180度的角是平角,小于180度的角是钝角。( )
四、解答题
16.三角形ABC中,∠A=90°,∠C=60°,∠CBA=30°。按顺时针方向旋转一个角度后得到三角形A′BC′,∠C′BA=90°(如图所示)。图中哪一点是旋转点?旋转了多少度?
17.已知∠ACB=60°,求:∠ACD=?
18.如图,已知∠1=36°,求∠2,∠3,∠4的度数。
19.如图,将1张圆形纸对折3次,得到的角分别是多少度
( ) ( ) ( )
20.将一块面积为225平方分米的正方形幕布向上卷起一部分.(如图)
卷起后,露出的面积是多少平方分米?(如图虚线部分)
参考答案:
1.B
【分析】等于180度的角是平角,据此解答。
【详解】平角是180度。
故答案为:B
【点睛】熟记平角的特征是解题关键。
2.C
【分析】钟面1大格是30°,当时针和分针之间较小的夹角有3大格时,30°×3=90°,此时是个直角;当时针和分针之间较小的夹角小于3大格时,此时是个锐角;当时针和分针之间较小的夹角大于3大格,小于6大格时(6×30°=180°),此时是个钝角。
【详解】9:30钟面上时针和分针形成的角大于3大格,小于6大格;3:00时针和分针形成的角等于3大格;
则9:30钟面上时针和分针形成的角是钝角,3:00时针和分针组成一个直角。
故答案为:C
【点睛】解答此题应结合题意,根据角的概念和分类进行解答。
3.B
【分析】分析图片可知:时针和分针形成的角是平角,据此选择即可解答。
【详解】钟面上,时针与分针所形成的角是平角;
故答案为:B
【点睛】此题考查钟面特征以及平角的认识。
4.D
【分析】∠1和∠3组成的角是平角,∠2和∠3组成的角也是平角,所以∠1=∠2;∠1和∠3组成的角是直角,∠2和∠3组成的角是直角,所以∠1=∠2;通过折叠可知∠1=∠2;∠1和∠3组成的角是平角,∠2和∠3组成的角也是平角,所以∠1=∠2。
【详解】∠1和∠2相等的一共有4幅。
故答案为:D
【点睛】本题考查角度的计算,理解平角和直角的度数是解决本题的关键。
5.B
【详解】试题分析:9时整,时钟的时针指向9,分针指向12,它们之间的格子数是15个,在钟面上每个格子对应的圆心角是360°÷60,求出时针和分针之间的角度,再根据角的分类进行解答.
解:360°÷60×15,
=6°×15,
=90°.
答:九时整,时钟的时针和分针成90°角.
故选B.
点评:本题的关键是先求出时针和分针之间的角度,再根据角的分类进行解答.
6. 3 90
【详解】略
7. 4 180
【分析】等于90°的角是直角;等于180°的角是平角;等于360°的角叫周角,据此解答。
【详解】根据分析可知:1周角=4直角;1平角=180°;
【点睛】熟记:一个直角=90°、一个平角=180°、一个周角=360°,所以,1周角=2平角,1周角=4直角。
8.360
【详解】试题分析:根据三角形的任意一个外角等于和它不相邻两内角和,及在同一直线上的角的度数是180度进行解答.
解:∠1=180°﹣40°﹣45°=95°,
∠2=40°+45°=85°,
∠3=180°﹣45°﹣75°=60°,
∠4=45°+75°=120°,
∠1+∠2+∠3+∠4=95°+85°+60°+120°=360°.
故答案为360.
点评:本题主要考查了学生根据平角,和三角形外角等于和它不相邻居的两内角解答问题的能力.
9.钝,360,30
【详解】试题分析:(1)钟面一周为360°,共分12大格,每格为360÷12=30°,下午4时整,分针与时针相差4个整大格,所以钟面上时针与分针形成的夹角是:30°×4=120°,由此根据钝角的定义即可解答.
(2)从4时到5时,是经历了1小时,所以分针正好旋转了一周,是360度;根据时钟上的时针匀速旋转一小时的度数为30°,即可得出1小时时针旋转的度数.
解:(1)30°×4=120°,所以时针与分针所成的角是钝角;
(2)因为时钟上的时针匀速旋转一周的度数为360°,时钟上的时针匀速旋转一周需要12小时,
则时钟上的时针匀速旋转一小时的度数为:360÷12=30°;
分针旋转1小时的度数为360°.
故答案为钝,360,30.
点评:本题要在了解钟面结构的基础上进行解答.
10.15
【分析】根据角的定义可知,图中单独的角有5个,由两个单独的角组成的角有4个,由三个单独的角组成的角有3个,由四个单独的角组成的角有2个,由五个单独的角组成的角有1个,则一共有5+4+3+2+1个角。
【详解】5+4+3+2+1=15(个)
则有15个角。
【点睛】从一点引出两条射线所形成的图形叫做角。这一点是角的顶点,两条射线是角的边。数角时,要按照顺序数,才能做到不重不漏。
11.×
【分析】角的大小与两边的长短无关,只与边叉开的大小有关,叉开得越大,角就越大,叉开越小,角就越小。
【详解】用放大10倍的放大镜看角,只是角的两边长度增大了,角的大小没变;
故答案为:×
【点睛】本题考查了角的概念和影响角的大小的因素。
12.×
【分析】等于180°的角叫平角,等于360°的角叫周角。360°是180°的几倍,1周角就等于几平角。
【详解】360°÷180°=2,1周角=2平角。
故答案为:×
【点睛】熟记周角、平角的特征是解题关键。
13.×
【详解】略
14.√
【分析】把角的两条边延长2倍,只改变可角两边的长度,没有改变角两边叉开的大小,则角的度数不变。
【详解】根据分析可知,把角的两条边延长2倍,角的大小不变。
故答案为:√。
【点睛】角的大小跟两边叉开的大小有关,跟边的长短无关。
15.×
【详解】略
16.点B是旋转点,三角形ABC绕点B顺时针旋转了60°。
【分析】1.旋转中心的确定分两种情况:
①旋转点若在图形上,哪一点在旋转过程中位置没有改变,哪一点就是旋转中心;
②若在图形外,所有对应点连线的中垂线的交点就是旋转中心。
2.图形旋转的度数等于旋转点所在的对应线段夹角的度数。
【详解】根据图形所示,三角形A′BC′是三角形ABC绕B点顺时针旋转得到的。依据旋转的特征和性质,∠A′BA的度数就是旋转的度数。∠CBA=30°,那么∠C′BA′=30°。又因∠C′BA=90°,故∠C′BA-∠C′BA′=90°-30°=60°,也就是三角形ABC绕点B顺时针旋转了60°。
【点睛】明确旋转前后的对应边及对应顶点是解题的关键。
17.120度
【详解】试题分析:由题意得:∠ACB和∠ACD组成一个平角,平角是180度,所以用180度减去∠ACB就是∠ACD的度数.
解:∠ACD=180°﹣∠ACB,
=180°﹣60°,
=120°.
答:∠ACD是120度.
点评:解决本题要灵活运用平角的特点.
18.∠2=144°
∠3=36°
∠4=144°
【分析】根据题图可知,∠1和∠2组成一个平角,则∠2=180°-∠1。∠2和∠3组成一个平角,则∠3=180°-∠2。∠1和∠4组成一个平角,则∠4=180°-∠1。
【详解】∠2=180°-36°=144°
∠3=180°-144°=36°
∠4=180°-36°=144°
【点睛】明确平角为180°是解决本题的关键。
19. 180° 90° 45°
【解析】略
20.75平方分米
【详解】试题分析:这个正方形幕布是一块边长为15分米的正方形,卷起后,露出的部分是一个长为正方形边长15分米,宽为5分米的长方形,根据长方形面积公式即可求出它的面积.
解:15×5=75(平方分米)
答:卷起后,露出的面积是75平方分米.
故答案为75平方分米.
点评:关键是弄明白露出的部分是一个长为正方形边长15分米,宽为5分米的长方形.根据“正方形幕布”与图中标出的数据15分米,即可解答,“面积为225平方分米”多余.或给出这块幕布的面积,说是长方形,根据标出的长求宽.
一、选择题
1.平角是( )度。
A.90 B.180 C.360
2.9:30钟面上时针和分针形成的角是( ),3:00时针和分针组成一个( )。
A.直角,钝角 B.直角,锐角 C.钝角,直角 D.直角,直角
3.左面钟面上,时针与分针所形成的角是( )。
A.周角 B.平角 C.直角 D.锐角
4.下面图中,∠1和∠2相等的一共有( )幅。
A.1 B.2 C.3 D.4
5.上午9时,时针与分针的夹角是( )
A.180° B.90° C.0°
二、填空题
6.30°角的 倍是直角, 度角的4倍是周角.
7.1周角=( )直角;1平角=( )°。
8.图中,∠1、∠2、∠3、∠4的和是 度.
9.下午4时,钟面上时针和分针所成的角是 角;从4时到5时,分针旋转了 度,时针旋转了 度.
10.数一数,填一填。
有( )个角。
三、判断题
11.用放大10倍的放大镜看的角,看到的角的度数是。( )
12.1周角=4平角。( )
13.小于90°的角叫做直角. ( )
14.把角的两条边延长2倍,角的大小不变。( )
15.180度的角是平角,小于180度的角是钝角。( )
四、解答题
16.三角形ABC中,∠A=90°,∠C=60°,∠CBA=30°。按顺时针方向旋转一个角度后得到三角形A′BC′,∠C′BA=90°(如图所示)。图中哪一点是旋转点?旋转了多少度?
17.已知∠ACB=60°,求:∠ACD=?
18.如图,已知∠1=36°,求∠2,∠3,∠4的度数。
19.如图,将1张圆形纸对折3次,得到的角分别是多少度
( ) ( ) ( )
20.将一块面积为225平方分米的正方形幕布向上卷起一部分.(如图)
卷起后,露出的面积是多少平方分米?(如图虚线部分)
参考答案:
1.B
【分析】等于180度的角是平角,据此解答。
【详解】平角是180度。
故答案为:B
【点睛】熟记平角的特征是解题关键。
2.C
【分析】钟面1大格是30°,当时针和分针之间较小的夹角有3大格时,30°×3=90°,此时是个直角;当时针和分针之间较小的夹角小于3大格时,此时是个锐角;当时针和分针之间较小的夹角大于3大格,小于6大格时(6×30°=180°),此时是个钝角。
【详解】9:30钟面上时针和分针形成的角大于3大格,小于6大格;3:00时针和分针形成的角等于3大格;
则9:30钟面上时针和分针形成的角是钝角,3:00时针和分针组成一个直角。
故答案为:C
【点睛】解答此题应结合题意,根据角的概念和分类进行解答。
3.B
【分析】分析图片可知:时针和分针形成的角是平角,据此选择即可解答。
【详解】钟面上,时针与分针所形成的角是平角;
故答案为:B
【点睛】此题考查钟面特征以及平角的认识。
4.D
【分析】∠1和∠3组成的角是平角,∠2和∠3组成的角也是平角,所以∠1=∠2;∠1和∠3组成的角是直角,∠2和∠3组成的角是直角,所以∠1=∠2;通过折叠可知∠1=∠2;∠1和∠3组成的角是平角,∠2和∠3组成的角也是平角,所以∠1=∠2。
【详解】∠1和∠2相等的一共有4幅。
故答案为:D
【点睛】本题考查角度的计算,理解平角和直角的度数是解决本题的关键。
5.B
【详解】试题分析:9时整,时钟的时针指向9,分针指向12,它们之间的格子数是15个,在钟面上每个格子对应的圆心角是360°÷60,求出时针和分针之间的角度,再根据角的分类进行解答.
解:360°÷60×15,
=6°×15,
=90°.
答:九时整,时钟的时针和分针成90°角.
故选B.
点评:本题的关键是先求出时针和分针之间的角度,再根据角的分类进行解答.
6. 3 90
【详解】略
7. 4 180
【分析】等于90°的角是直角;等于180°的角是平角;等于360°的角叫周角,据此解答。
【详解】根据分析可知:1周角=4直角;1平角=180°;
【点睛】熟记:一个直角=90°、一个平角=180°、一个周角=360°,所以,1周角=2平角,1周角=4直角。
8.360
【详解】试题分析:根据三角形的任意一个外角等于和它不相邻两内角和,及在同一直线上的角的度数是180度进行解答.
解:∠1=180°﹣40°﹣45°=95°,
∠2=40°+45°=85°,
∠3=180°﹣45°﹣75°=60°,
∠4=45°+75°=120°,
∠1+∠2+∠3+∠4=95°+85°+60°+120°=360°.
故答案为360.
点评:本题主要考查了学生根据平角,和三角形外角等于和它不相邻居的两内角解答问题的能力.
9.钝,360,30
【详解】试题分析:(1)钟面一周为360°,共分12大格,每格为360÷12=30°,下午4时整,分针与时针相差4个整大格,所以钟面上时针与分针形成的夹角是:30°×4=120°,由此根据钝角的定义即可解答.
(2)从4时到5时,是经历了1小时,所以分针正好旋转了一周,是360度;根据时钟上的时针匀速旋转一小时的度数为30°,即可得出1小时时针旋转的度数.
解:(1)30°×4=120°,所以时针与分针所成的角是钝角;
(2)因为时钟上的时针匀速旋转一周的度数为360°,时钟上的时针匀速旋转一周需要12小时,
则时钟上的时针匀速旋转一小时的度数为:360÷12=30°;
分针旋转1小时的度数为360°.
故答案为钝,360,30.
点评:本题要在了解钟面结构的基础上进行解答.
10.15
【分析】根据角的定义可知,图中单独的角有5个,由两个单独的角组成的角有4个,由三个单独的角组成的角有3个,由四个单独的角组成的角有2个,由五个单独的角组成的角有1个,则一共有5+4+3+2+1个角。
【详解】5+4+3+2+1=15(个)
则有15个角。
【点睛】从一点引出两条射线所形成的图形叫做角。这一点是角的顶点,两条射线是角的边。数角时,要按照顺序数,才能做到不重不漏。
11.×
【分析】角的大小与两边的长短无关,只与边叉开的大小有关,叉开得越大,角就越大,叉开越小,角就越小。
【详解】用放大10倍的放大镜看角,只是角的两边长度增大了,角的大小没变;
故答案为:×
【点睛】本题考查了角的概念和影响角的大小的因素。
12.×
【分析】等于180°的角叫平角,等于360°的角叫周角。360°是180°的几倍,1周角就等于几平角。
【详解】360°÷180°=2,1周角=2平角。
故答案为:×
【点睛】熟记周角、平角的特征是解题关键。
13.×
【详解】略
14.√
【分析】把角的两条边延长2倍,只改变可角两边的长度,没有改变角两边叉开的大小,则角的度数不变。
【详解】根据分析可知,把角的两条边延长2倍,角的大小不变。
故答案为:√。
【点睛】角的大小跟两边叉开的大小有关,跟边的长短无关。
15.×
【详解】略
16.点B是旋转点,三角形ABC绕点B顺时针旋转了60°。
【分析】1.旋转中心的确定分两种情况:
①旋转点若在图形上,哪一点在旋转过程中位置没有改变,哪一点就是旋转中心;
②若在图形外,所有对应点连线的中垂线的交点就是旋转中心。
2.图形旋转的度数等于旋转点所在的对应线段夹角的度数。
【详解】根据图形所示,三角形A′BC′是三角形ABC绕B点顺时针旋转得到的。依据旋转的特征和性质,∠A′BA的度数就是旋转的度数。∠CBA=30°,那么∠C′BA′=30°。又因∠C′BA=90°,故∠C′BA-∠C′BA′=90°-30°=60°,也就是三角形ABC绕点B顺时针旋转了60°。
【点睛】明确旋转前后的对应边及对应顶点是解题的关键。
17.120度
【详解】试题分析:由题意得:∠ACB和∠ACD组成一个平角,平角是180度,所以用180度减去∠ACB就是∠ACD的度数.
解:∠ACD=180°﹣∠ACB,
=180°﹣60°,
=120°.
答:∠ACD是120度.
点评:解决本题要灵活运用平角的特点.
18.∠2=144°
∠3=36°
∠4=144°
【分析】根据题图可知,∠1和∠2组成一个平角,则∠2=180°-∠1。∠2和∠3组成一个平角,则∠3=180°-∠2。∠1和∠4组成一个平角,则∠4=180°-∠1。
【详解】∠2=180°-36°=144°
∠3=180°-144°=36°
∠4=180°-36°=144°
【点睛】明确平角为180°是解决本题的关键。
19. 180° 90° 45°
【解析】略
20.75平方分米
【详解】试题分析:这个正方形幕布是一块边长为15分米的正方形,卷起后,露出的部分是一个长为正方形边长15分米,宽为5分米的长方形,根据长方形面积公式即可求出它的面积.
解:15×5=75(平方分米)
答:卷起后,露出的面积是75平方分米.
故答案为75平方分米.
点评:关键是弄明白露出的部分是一个长为正方形边长15分米,宽为5分米的长方形.根据“正方形幕布”与图中标出的数据15分米,即可解答,“面积为225平方分米”多余.或给出这块幕布的面积,说是长方形,根据标出的长求宽.
同课章节目录
