余角与补角[上学期]
图片预览


文档简介
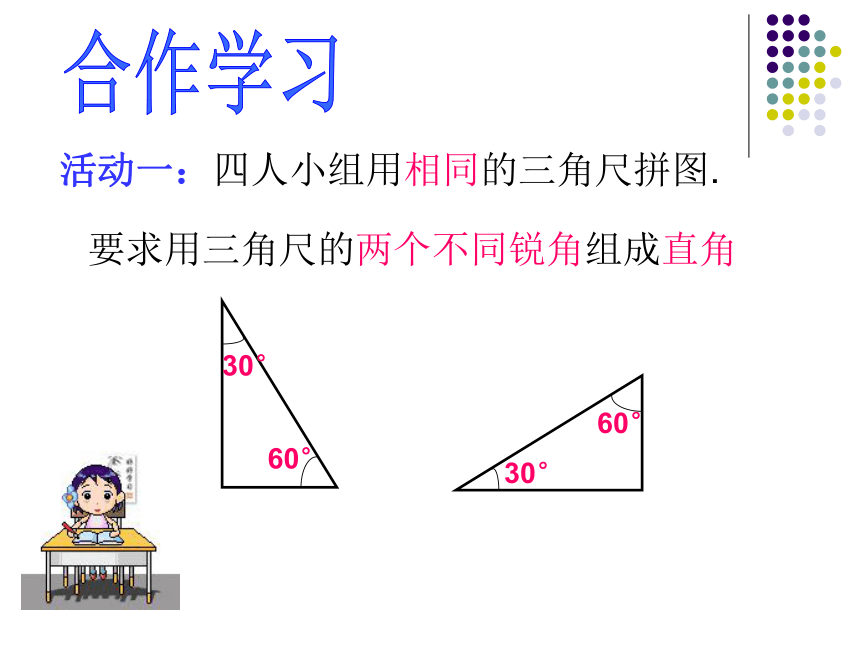
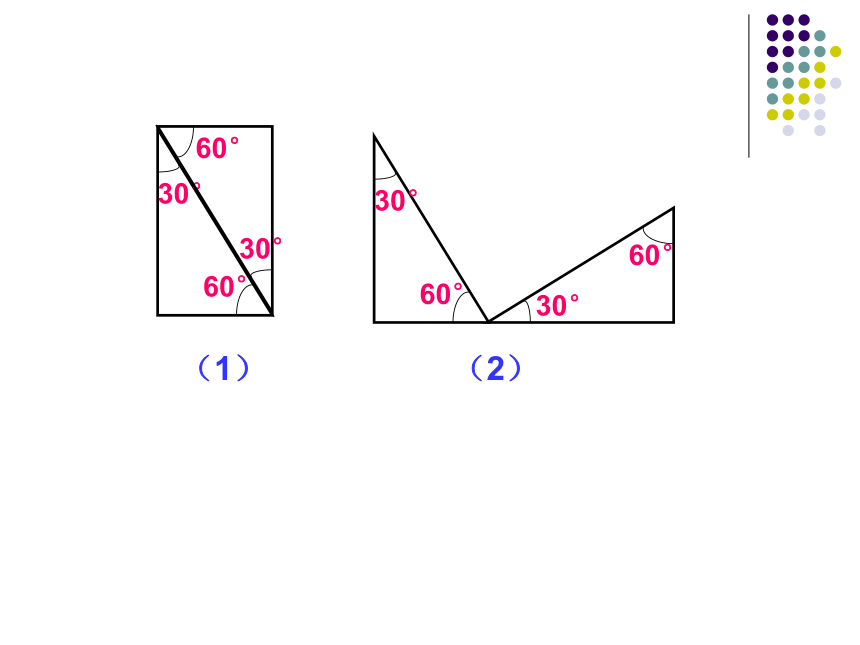
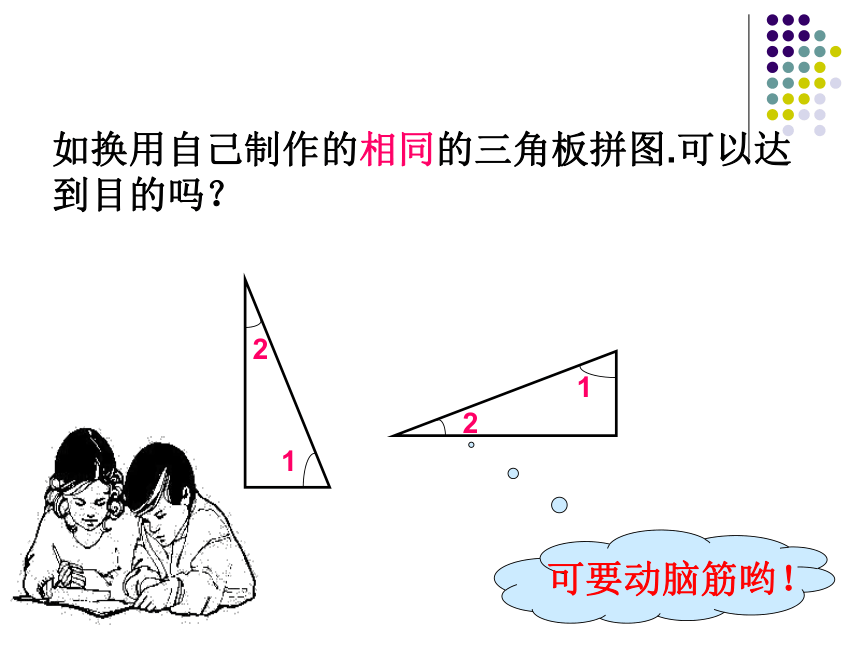
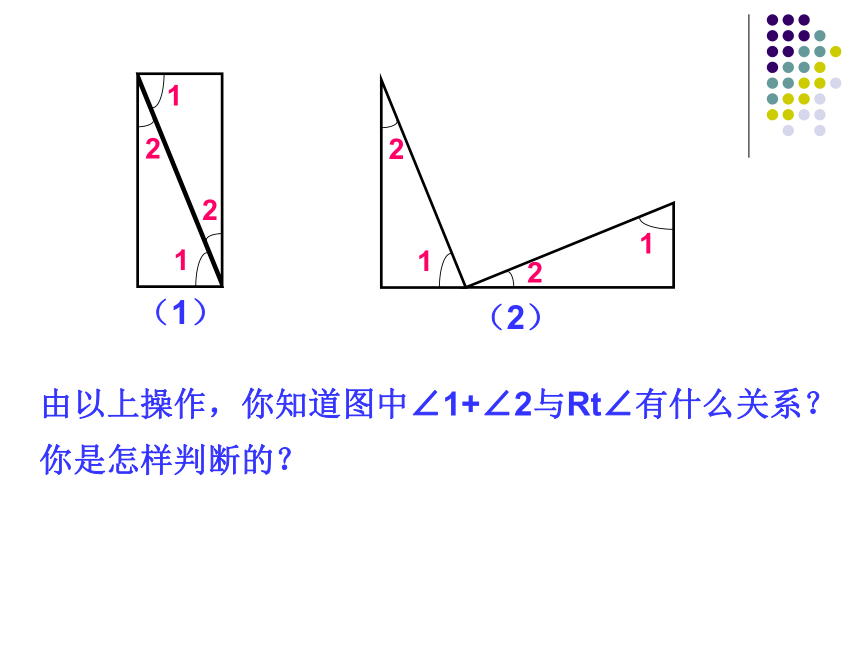
课件21张PPT。合作学习活动一:四人小组用相同的三角尺拼图.要求用三角尺的两个不同锐角组成直角(1)(2)如换用自己制作的相同的三角板拼图.可以达到目的吗?(1)(2)由以上操作,你知道图中∠1+∠2与Rt∠有什么关系?
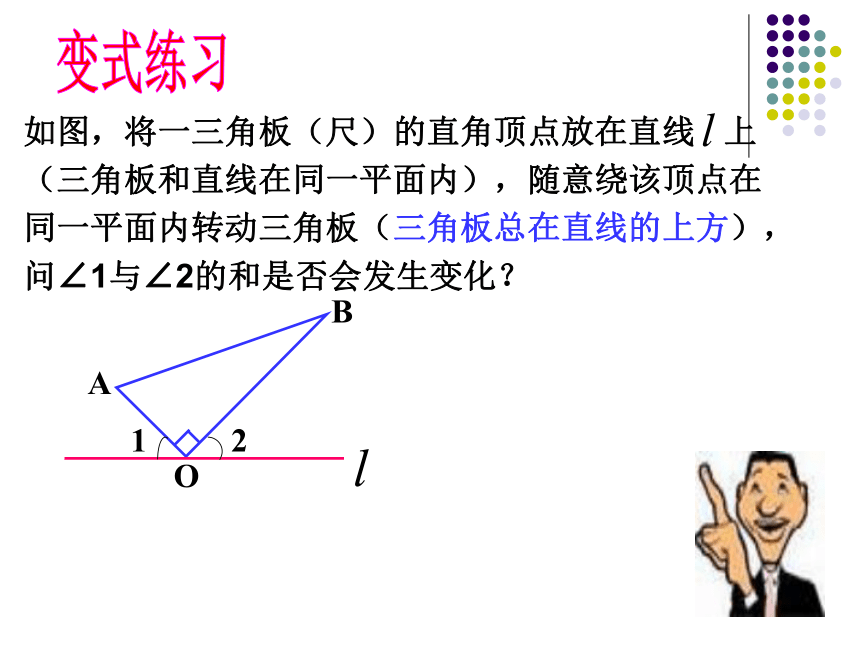
你是怎样判断的?变式练习如图,将一三角板(尺)的直角顶点放在直线 上
(三角板和直线在同一平面内),随意绕该顶点在
同一平面内转动三角板(三角板总在直线的上方),
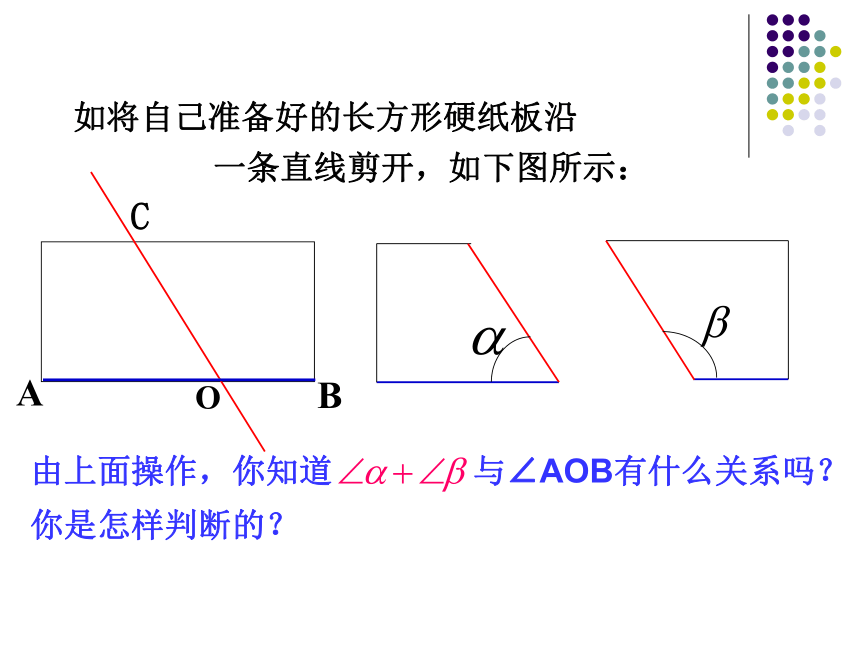
问∠1与∠2的和是否会发生变化?如将自己准备好的长方形硬纸板沿
一条直线剪开,如下图所示:由上面操作,你知道 与∠AOB有什么关系吗?
你是怎样判断的?余角和补角一、余角和补角的概念:(1)如果两个锐角的和是一个直角,称这两个锐角是互为余角,简称互余.其中一个角是另一个角的余角.(2)如果两个角的和是一个平角,称这两个角为互为补角简称互补. ∵ ∠α和 ∠β互补,
∴∠α+ ∠β=180°.∵∠α+ ∠β=180°,
∴∠α和 ∠β互补.∵∠α+ ∠β=90°,
∴∠α和 ∠β互余.∵ ∠α和 ∠β互余,
∴∠α+ ∠β=90°.数量关系为:数量关系为:其中一个角是另一个角的补角.问:①互余的两个角分别是什么角?②互补的两个角分别是什么角? 锐角 一个为锐角,另一个为钝角
或两个都是直角看谁答得快60 °150 °48 °138 °36 °126 °27 ° 37 ′117 ° 37 ′注意: 只有锐角有余角需要注意的几点: ①互余与互补是指两个角之间的关系,说单独的
一个角是余角或补角是毫无意义的,但可以说
一个角是某一个角的余角或补角.②两个角是否互余或互补只跟这两个角的大小有关,
与它们的位置无关,不要误认为互余或互补的角
必须相邻.(3)如果一个角的余角和补角都存在,那么这
个角的余角一定比这个角的补角小.(2)如果两个角互补,那么这两个角中,一个
是锐角,另一个是钝角;(1)一个锐角的补角一定是钝角;1、判断下列说法是否正确,并说明理由.基础练习√√(1) 动手画一画: 已知∠α(如图),请利用三角尺画的∠α的余角(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?(3) 这一结论用文字怎么叙述?同 角的余角相等(1) 动手画一画: 已知∠α(如图),请利用三角板画的∠α的余角(1) 动手画一画: 已知∠α(如图),请利用三角尺画的∠α的余角(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?(3) 这一结论用文字怎么叙述?同 角的余角相等(等)又因为∠α=∠β(1) 动手画一画: 已知∠α(如图),请利用三角板画的∠α的余角同 角的补角相等(等)(2) 动手画一画
已知∠α(如图),
请利用三角板画的∠α的补角3、下图中,Rt∠AOB的顶点在直线CD上,
根据前面的探究,图中有哪些角互余?
哪些角互补?说明你的理由.例2、如图,已知 .
指出图中还有哪些角相等,并说明理由.变式练习若将例2中射线OA反向延长,其它条件
保持不变,得到下图,问:解:∠AOB=∠COD.
理由:∵∠AOC=∠BOD=Rt∠,
∴∠AOB+∠BOC=90°,
∠COD+∠BOC=90°,
即∠AOB与∠COD都是∠BOC的余角,
∴∠AOB=∠COD(同角的余角相等).比一比 : 看谁快 互补的角 1. 如图A、O、 B在同一直线上,
∠AOC= ∠DOE=
找出图中 ∠2=∠4 , ∠AOC=∠BOC=∠DOE=900 ∠1=∠3 互余的角 相等的角∠1∠3∠AOE∠DOBC试一试:看谁会 2. 如图A、O、 B在同一直线上, ∠AOC= ∠DOE=
若∠1= 2∠3,求:∠2的度数解:设∠3 =x,则∠1=2X∵∠1+∠DOE+∠3=1800答: ∠2的度数为30度∴∠2=∠3(同角的余角相等)例3、已知一个角的补角是这个角的余角
的4倍,求这个角的度数.变式练习若一个角的补角和这个角的余角互补,
求这个角.解:设这个角为 度,则这个角的余角是
度,补角是 度。由题意,得
解这个方程,得答:这个角的度数为60°.衷心感谢你们的合作!
你是怎样判断的?变式练习如图,将一三角板(尺)的直角顶点放在直线 上
(三角板和直线在同一平面内),随意绕该顶点在
同一平面内转动三角板(三角板总在直线的上方),
问∠1与∠2的和是否会发生变化?如将自己准备好的长方形硬纸板沿
一条直线剪开,如下图所示:由上面操作,你知道 与∠AOB有什么关系吗?
你是怎样判断的?余角和补角一、余角和补角的概念:(1)如果两个锐角的和是一个直角,称这两个锐角是互为余角,简称互余.其中一个角是另一个角的余角.(2)如果两个角的和是一个平角,称这两个角为互为补角简称互补. ∵ ∠α和 ∠β互补,
∴∠α+ ∠β=180°.∵∠α+ ∠β=180°,
∴∠α和 ∠β互补.∵∠α+ ∠β=90°,
∴∠α和 ∠β互余.∵ ∠α和 ∠β互余,
∴∠α+ ∠β=90°.数量关系为:数量关系为:其中一个角是另一个角的补角.问:①互余的两个角分别是什么角?②互补的两个角分别是什么角? 锐角 一个为锐角,另一个为钝角
或两个都是直角看谁答得快60 °150 °48 °138 °36 °126 °27 ° 37 ′117 ° 37 ′注意: 只有锐角有余角需要注意的几点: ①互余与互补是指两个角之间的关系,说单独的
一个角是余角或补角是毫无意义的,但可以说
一个角是某一个角的余角或补角.②两个角是否互余或互补只跟这两个角的大小有关,
与它们的位置无关,不要误认为互余或互补的角
必须相邻.(3)如果一个角的余角和补角都存在,那么这
个角的余角一定比这个角的补角小.(2)如果两个角互补,那么这两个角中,一个
是锐角,另一个是钝角;(1)一个锐角的补角一定是钝角;1、判断下列说法是否正确,并说明理由.基础练习√√(1) 动手画一画: 已知∠α(如图),请利用三角尺画的∠α的余角(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?(3) 这一结论用文字怎么叙述?同 角的余角相等(1) 动手画一画: 已知∠α(如图),请利用三角板画的∠α的余角(1) 动手画一画: 已知∠α(如图),请利用三角尺画的∠α的余角(2)图中∠α的余角∠1,∠2的大小有什么关系?为什么?(3) 这一结论用文字怎么叙述?同 角的余角相等(等)又因为∠α=∠β(1) 动手画一画: 已知∠α(如图),请利用三角板画的∠α的余角同 角的补角相等(等)(2) 动手画一画
已知∠α(如图),
请利用三角板画的∠α的补角3、下图中,Rt∠AOB的顶点在直线CD上,
根据前面的探究,图中有哪些角互余?
哪些角互补?说明你的理由.例2、如图,已知 .
指出图中还有哪些角相等,并说明理由.变式练习若将例2中射线OA反向延长,其它条件
保持不变,得到下图,问:解:∠AOB=∠COD.
理由:∵∠AOC=∠BOD=Rt∠,
∴∠AOB+∠BOC=90°,
∠COD+∠BOC=90°,
即∠AOB与∠COD都是∠BOC的余角,
∴∠AOB=∠COD(同角的余角相等).比一比 : 看谁快 互补的角 1. 如图A、O、 B在同一直线上,
∠AOC= ∠DOE=
找出图中 ∠2=∠4 , ∠AOC=∠BOC=∠DOE=900 ∠1=∠3 互余的角 相等的角∠1∠3∠AOE∠DOBC试一试:看谁会 2. 如图A、O、 B在同一直线上, ∠AOC= ∠DOE=
若∠1= 2∠3,求:∠2的度数解:设∠3 =x,则∠1=2X∵∠1+∠DOE+∠3=1800答: ∠2的度数为30度∴∠2=∠3(同角的余角相等)例3、已知一个角的补角是这个角的余角
的4倍,求这个角的度数.变式练习若一个角的补角和这个角的余角互补,
求这个角.解:设这个角为 度,则这个角的余角是
度,补角是 度。由题意,得
解这个方程,得答:这个角的度数为60°.衷心感谢你们的合作!
