人教版数学八年级上册 13.1.2 第1课时 线段垂直平分线的性质和判定 课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.1.2 第1课时 线段垂直平分线的性质和判定 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
13.1.2 线段的垂直平分线的性质
第1课时 线段垂直平分线
的性质与判定
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
M
B
A
N
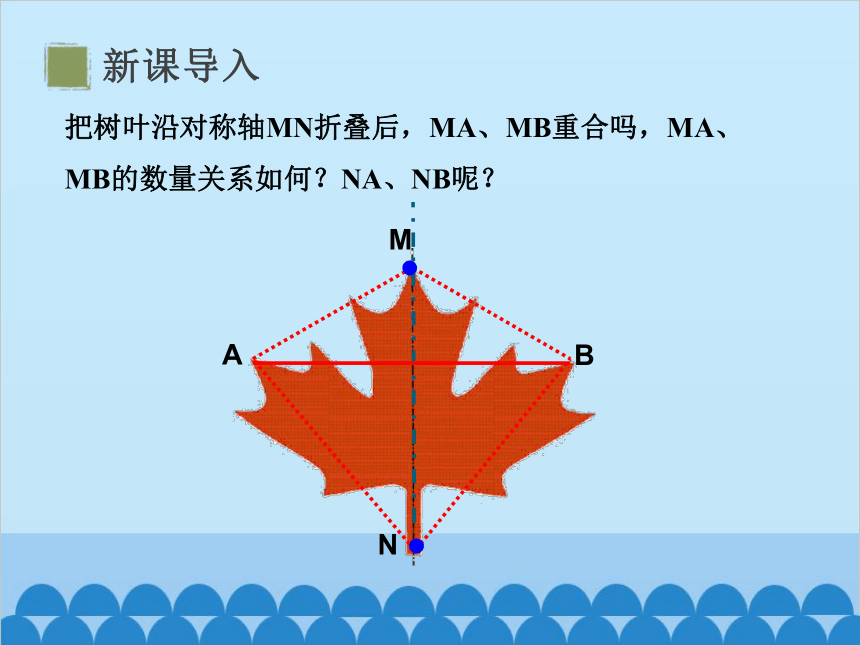
把树叶沿对称轴MN折叠后,MA、MB重合吗,MA、MB的数量关系如何?NA、NB呢?
新课导入
讲授新知
贰
为解决上面问题我们研究如下:如图所示,直线l垂直平分线段AB,P1、P2、P3、…是l 上的点,请你量一量线段P1A、P1B、P2A、P2B、P3A、P3B的长,你能发现什么?请猜想点P1、P2、P3、… 到点A 与点B 的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
知识点1 线段垂直平分线的性质
【猜想】点P1、P2、P3、… 到点A 与点B 的距离分
别相等.
由此你能得到什么结论?
线段的垂直平分线的性质:线段垂直平分线上的点和这条线段两个端点的距离相等.
讲授新知
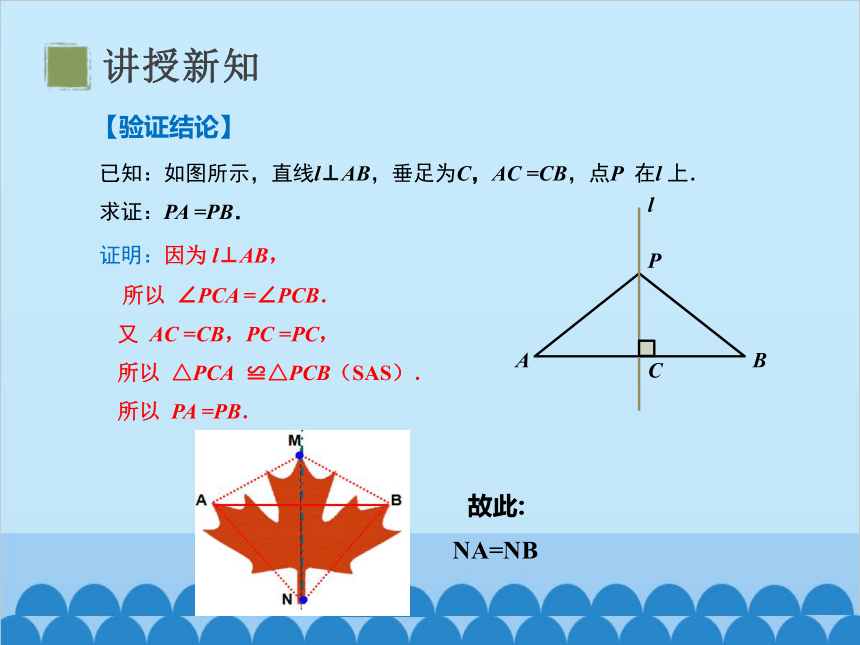
已知:如图所示,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:因为 l⊥AB,
所以 ∠PCA =∠PCB.
又 AC =CB,PC =PC,
所以 △PCA ≌△PCB(SAS).
所以 PA =PB.
P
A
B
l
C
【验证结论】
故此: NA=NB
讲授新知
例1 如图所示,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm B.10cmC.15cmD.17.5cm
C
方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
范例应用
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图所示,在△ABP中,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
C
知识点2 线段垂直平分线的判定
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
因为 PA =PB,PC =PC,
所以 Rt△PCA ≌Rt△PCB(HL).
所以 AC =BC.
又 PC⊥AB,
所以 点P 在线段AB 的垂直平分线上.
讲授新知
线段垂直平分线的判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
应用格式:
因为PA =PB,
所以点P 在AB 的垂直平分线上.
P
A
B
归纳:1.线段的垂直平分线是到线段两端点的距离相等的点的集合;
2.判断一个点是否在线段的垂直平分线上.
讲授新知
解:因为AB =AC,
所以点A 在BC 的垂直平分线上.
因为MB =MC,
因为点M 在BC 的垂直平分线上,
所以直线AM 是线段BC 的垂直
平分线.
例2 如图所示,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
范例应用
当堂训练
叁
当堂训练
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD; B .CD垂直平分AB ;
C.AB与CD互相垂直平分; D.CD平分∠ ACB .
2.到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三边高线的交点 D.没有这样的点
3.如图所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为 .
4.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
A
B
5
16
5.如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
因为OE平分∠AOB,EC⊥OA,ED⊥OB,
所以DE=CE.
因为点E是∠AOB的平分线上一点,
所以∠DOE=∠COE,
因为EC⊥OA,ED⊥OB,所以∠ODE=∠OCE=90°,
所以△OED≌△OEC(AAS),所以OC=OD;
所以 OE是CD的垂直平分线.
当堂训练
课堂小结
肆
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
判定
线段的垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
课堂小结
内容
内容
作用
作用
课后作业
基础题:1.课后习题 P65第 6题。
提高题:2.请学有余力的同学P66 T13
谢
谢
13.1.2 线段的垂直平分线的性质
第1课时 线段垂直平分线
的性质与判定
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
M
B
A
N
把树叶沿对称轴MN折叠后,MA、MB重合吗,MA、MB的数量关系如何?NA、NB呢?
新课导入
讲授新知
贰
为解决上面问题我们研究如下:如图所示,直线l垂直平分线段AB,P1、P2、P3、…是l 上的点,请你量一量线段P1A、P1B、P2A、P2B、P3A、P3B的长,你能发现什么?请猜想点P1、P2、P3、… 到点A 与点B 的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
知识点1 线段垂直平分线的性质
【猜想】点P1、P2、P3、… 到点A 与点B 的距离分
别相等.
由此你能得到什么结论?
线段的垂直平分线的性质:线段垂直平分线上的点和这条线段两个端点的距离相等.
讲授新知
已知:如图所示,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
证明:因为 l⊥AB,
所以 ∠PCA =∠PCB.
又 AC =CB,PC =PC,
所以 △PCA ≌△PCB(SAS).
所以 PA =PB.
P
A
B
l
C
【验证结论】
故此: NA=NB
讲授新知
例1 如图所示,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm B.10cmC.15cmD.17.5cm
C
方法归纳:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
范例应用
反过来,如果PA =PB,那么点P 是否在线段AB 的垂直平分线上呢?
点P 在线段AB 的垂直平分线上.
已知:如图所示,在△ABP中,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
P
A
B
C
知识点2 线段垂直平分线的判定
证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
因为 PA =PB,PC =PC,
所以 Rt△PCA ≌Rt△PCB(HL).
所以 AC =BC.
又 PC⊥AB,
所以 点P 在线段AB 的垂直平分线上.
讲授新知
线段垂直平分线的判定
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
应用格式:
因为PA =PB,
所以点P 在AB 的垂直平分线上.
P
A
B
归纳:1.线段的垂直平分线是到线段两端点的距离相等的点的集合;
2.判断一个点是否在线段的垂直平分线上.
讲授新知
解:因为AB =AC,
所以点A 在BC 的垂直平分线上.
因为MB =MC,
因为点M 在BC 的垂直平分线上,
所以直线AM 是线段BC 的垂直
平分线.
例2 如图所示,AB =AC,MB =MC.直线AM 是线段BC 的垂直平分线吗?
A
B
C
D
M
范例应用
当堂训练
叁
当堂训练
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD; B .CD垂直平分AB ;
C.AB与CD互相垂直平分; D.CD平分∠ ACB .
2.到三角形三个顶点的距离相等的点是( )
A.三条角平分线的交点 B.三边垂直平分线的交点
C.三边高线的交点 D.没有这样的点
3.如图所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为 .
4.如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
A
B
5
16
5.如图所示,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
因为OE平分∠AOB,EC⊥OA,ED⊥OB,
所以DE=CE.
因为点E是∠AOB的平分线上一点,
所以∠DOE=∠COE,
因为EC⊥OA,ED⊥OB,所以∠ODE=∠OCE=90°,
所以△OED≌△OEC(AAS),所以OC=OD;
所以 OE是CD的垂直平分线.
当堂训练
课堂小结
肆
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
判定
线段的垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
课堂小结
内容
内容
作用
作用
课后作业
基础题:1.课后习题 P65第 6题。
提高题:2.请学有余力的同学P66 T13
谢
谢
