人教B版高中数学选择性必修第二册期末综合测试卷(Word含解析)
文档属性
| 名称 | 人教B版高中数学选择性必修第二册期末综合测试卷(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 98.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 10:21:54 | ||
图片预览




文档简介
人教B版高中数学选择性必修第二册期末综合测试卷
时间:120分钟 满分:150分
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某车间加工某种机器的零件数x(单位:个)与加工这些零件所花费的时间y(单位:min)之间的对应数据如下表所示:
x/个 10 20 30 40 50
y/min 62 68 75 81 89
由表中的数据可得回归直线方程=x+54.9,则加工70个零件比加工60个零件大约多用( )
A.5.8 min B.6 min C.6.7 min D.8 min
2.已知服从正态分布N(μ,σ2)的随机变量在区间(μ-σ,μ+σ],(μ-2σ,μ+2σ]和(μ-3σ,μ+3σ]内取值的概率分别为68.26%,95.44%和99.74%.若某校高二年级1 000名学生的某次考试成绩X服从正态分布N(90,152),则此次考试成绩在区间(105,120]内的学生大约有( )
A.477人 B.136人 C.341人 D.131人
3.围棋起源于中国,据先秦典籍《世本》记载“尧造围棋,丹朱善之”,围棋至今已有四千多年历史,蕴含着中华文化的丰富内涵.在某次国际围棋比赛中,甲、乙两人进入最后决赛.比赛采取五局三胜制,即先胜三局的一方获得比赛冠军(假设没有平局),比赛结束假设每局比赛乙胜甲的概率都为,且各局比赛的胜负互不影响,则在不超过4局的比赛中甲获得冠军的概率为( )
A. B. C. D.
4.在(2+x)6(1+y)m的展开式中,令x3y的系数为800,则含xy4项的系数为( )
A.30 B.960 C.300 D.360
5.2021年某地电视台春晚的戏曲节目,准备了经典京剧、豫剧、越剧、粤剧、黄梅戏、评剧6个剧种的各一个片段.对这6个剧种的演出顺序有如下要求:京剧必须排在前三,且越剧、粤剧必须排在一起,则该戏曲节目演出顺序共有( )
A.120种 B.156种 C.188种 D.240种
6.在某电视台有一闯关节目,该节目设置有两关,闯关规则是:当第一关闯关成功后,方可进入第二关.为了调查闯关的难度,该电视台调查了参加过此节目的100名选手的闯关情况,第一关闯关成功的有80人,第一关闯关成功且第二关闯关也成功的选手有72人,以闯关成功的频率近似作为闯关成功的概率,已知某个选手第一关闯关成功,则该选手第二关闯关成功的概率为( )
A.0.72 B.0.8 C.0.9 D.0.576
7.用5种不同颜色给图中5个车站的候车牌(E,A,B,C,D)染色,要求相邻的两个车站间的候车牌不同色,染色方法有( )
A.120种 B.180种 C.360种 D.420种
8.已知(x-2)8=a0+a1x+a2x2+…+a8x8,则下列结论不正确的是( )
A.a0=28 B.a8=1
C.a1+a2+…+a8=1 D.a0-a1+a2-…+a8=38
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.某校共有东门、西门、北门三道校门.由于疫情防控需要,学校安排甲、乙、丙、丁4名教师志愿者分别去三道校门协助保安值守,下列选项正确的是( )
A.若对每名教师志愿者去哪道校门无要求,则共有81种不同的安排方法
B.若恰有一道门没有教师志愿者去,则共有42种不同的安排方法
C.若甲、乙两人都不能去北门,且每道门都有教师志愿者去,则共有44种不同的安排方法
D.若学校新购入20把同一型号的额温枪,准备全部分配给三道校门使用,每道校门至少3把,则共有78种分配方法
10.下列说法正确的是( )
A.抛掷两枚质地均匀的骰子,至少有一枚骰子的点数是3的概率为
B.甲乙两人独立地解题,已知各人能解出的概率分别是,,则题被解出的概率是
C.某小组由5名学生组成,其中3名男生,2名女生,现从中任选两名学生参加演讲比赛,至少有一名男生与至少有一名女生是互斥事件
D.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是
11.已知随机变量X~N(2,σ2),且P(1A.P(2C.P(0P(212.下列说法正确的是( )
A.若事件A与B互相独立,且0B.设随机变量X服从正态分布N(0,1),则P(|x|<)=1-2P(X<)
C.在回归分析中,对一组给定的样本数据(x1,y1),(x2,y2),…,(xn,yn)而言,若残差平方和越大,则模型的拟合效果越差;反之,则模型的拟合效果越好
D.若随机变量ξ服从二项分布B(4,),则E(2ξ+3)=5
三、填空题:本题共4小题,每小题5分,共20分.
13.在二项式(2x3+)n的展开式中,所有的二项式系数之和为64,则该展开式中的x6的系数是________.
14.已知随机变量X服从二项分布B(12,0.25),且E(aX-3)=3(a∈R),则D(aX-3)=________.
15.某商场在儿童节举行回馈顾客活动,凡在商场消费满100元者即可参加射击赢玩具活动,具体规则如下:每人最多可射击3次,一旦击中,则可获奖且不再继续射击,否则一直射击到3次为止.设甲每次击中的概率为p(p≠0),射击次数为Y,若Y的数学期望E(Y)>,则p的取值范围是________.
16.在是否接种疫苗的调查中调查了7人,7人中有4人未接种疫苗,3人接种了疫苗,从这7人中随机抽取3人进行身体检查,用X表示抽取的3人中未接种疫苗的人数,则随机变量X的数学期望为________,设A为事件“抽取的3人中,既有接种疫苗的人,也有未接种疫苗的人”,则事件A发生的概率为________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)某网站规定:一个邮箱在一天内出现3次密码尝试错误,该邮箱将被锁定24小时.小王发现自己忘记了邮箱密码,但是可以确定该邮箱的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该邮箱被锁定.
(1)求当天小王的该邮箱被锁定的概率;
(2)设当天小王尝试该邮箱的密码次数为X,求X的分布列及E(X),D(X)的值.
18.(12分)为迎接2022年8月8日至8月18日在六盘水市举行的贵州省第十一届运动会,运动员们正艰苦训练,积极备战.某运动员射击一次所得环数X的分布列如下:
X 8 9 10
P 0.4 0.4 0.2
现进行两次射击,且两次射击互不影响,以该运动员两次射击中最高环数作为他的成绩,记为ξ.
(1)求此人两次命中环数相同的概率;
(2)求ξ的分布列和数学期望E(ξ).
19.(12分)在“双减”政策背景之下,某校就推进学校、家庭、社会体育教育的“一体化”,实现“教会、勤练、常赛”的核心任务.学校组织人员对在校学生“是否喜爱运动”做了一次随机调查.共随机调查了18名男生和12名女生,调查发现,男、女生中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下2×2列联表:根据小概率值α=0.1的χ2独立性检验,能否据此推断性别与喜爱运动有关?
喜欢运动 不喜欢运动 总计
男
女
总计
(2)从被调查的女生中抽取3人,若其中喜爱运动的人数为ξ,求ξ的分布列.
附参考公式及参考数据:
α=P(χ2≥k) 0.40 0.25 0.10 0.010
k 0.708 1.323 2.706 6.635
χ2=,其中n=a+b+c+d.
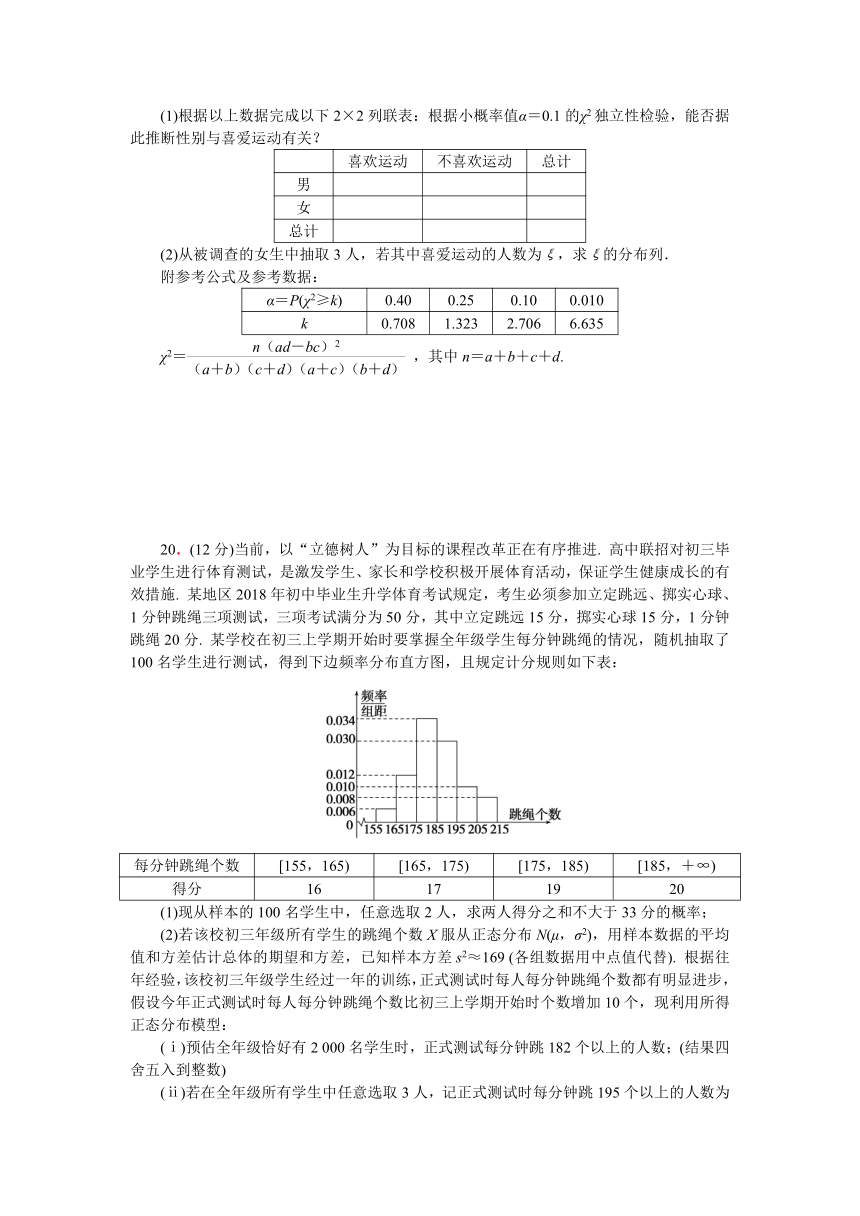
20.(12分)当前,以“立德树人”为目标的课程改革正在有序推进. 高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施. 某地区2018年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分为50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分. 某学校在初三上学期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数 [155,165) [165,175) [175,185) [185,+∞)
得分 16 17 19 20
(1)现从样本的100名学生中,任意选取2人,求两人得分之和不大于33分的概率;
(2)若该校初三年级所有学生的跳绳个数X服从正态分布N(μ,σ2),用样本数据的平均值和方差估计总体的期望和方差,已知样本方差s2≈169 (各组数据用中点值代替). 根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
(ⅰ)预估全年级恰好有2 000名学生时,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
(ⅱ)若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195个以上的人数为ξ,求随机变量ξ的分布列和期望.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ21.(12分)某商店欲购进某种食品(保质期为两天),且该商店每两天购进该食品一次(购进时,该食品是刚生产的).根据市场调查,该食品每份进价8元,售价12元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响.为了解市场的需求情况,现统计该食品在本地区100天的销售量,如下表:
销售量(份) 15 16 17 18
天数 20 30 40 10
(1)根据该食品在本地区100天的销售量统计表,记两天一共销售该食品的份数为ξ,求ξ的分布列与数学期望;(视样本频率为概率)
(2)以两天内该食品所获得的利润的数学期望为决策依据,若该商店计划一次性购进32份或33份该食品,试判断哪一种获得的利润更高.
22.(12分)新冠肺炎疫情发生以来,我国某科研机构开展应急科研攻关,研制了一种新型冠状病毒疫苗,并已进入二期临床试验.根据普遍规律,志愿者接种疫苗后体内会产生抗体,人体中检测到抗体,说明有抵御病毒的能力.通过检测,用x表示注射疫苗后的天数,y表示人体中抗体含量水平(单位:miu/mL,即:百万国际单位/毫升),现测得某志愿者的相关数据如下表所示.
天数x 1 2 3 4 5 6
抗体含量水平y 5 10 26 50 96 195
根据以上数据,绘制了散点图.
(1)根据散点图判断,y=c·edx与y=a+bx(a,b,c,d均为大于0的实数),哪一个更适宜作为描述y与x关系的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果求出y关于x的回归方程,并预测该志愿者在注射疫苗后的第10天的抗体含量水平值;
(3)从这位志愿者的前6天的检测数据中随机抽取3天的数据作进一步的分析,求其中的y值小于50的天数X的分布列及数学期望.
参考数据:其中w=ln y.
(xi-)2 (wi-)2 (wi-)(xi-) (xi-)(yi-) e8.3
3.50 63.67 3.49 17.50 9.49 12.95 519.01 4 023.87
参考公式:==,=-.
参考答案与解析
1.答案:C
解析:由表中的数据,得==30,
==75,
将,代入=x+54.9,得=0.67,
所以加工70个零件比加工60个零件大约多用70+54.9-(60+54.9)=10=6.7 min.故选C.
2.答案:B
解析:根据题意,P(105=
=
=0.135 9,
则1 000×0.135 9=135.9≈136,
故此次考试成绩在区间(105,120]内的学生大约有136人.
故选B.
3.答案:A
解析:在不超过4局的比赛中甲获得冠军包含两种情况,且两种情况互斥:
①甲前三局全胜,概率为P1=()3=;
②前三局甲两胜一负,第四局甲胜,概率为
P2=C()2()()=.
∴在不超过4局的比赛中甲获得冠军的概率为
P=P1+P2=+=.故选A.
4.答案:B
解析:(2+x)6展开式中x3的系数为C×23,(1+y)m展开式中y的系数为C,
所以x3y的系数为C×23×C,
所以C×23×C=800,即160m=800,解得m=5,
所以(2+x)6展开式中x的系数为C×25,(1+y)5展开式中y4的系数为C,
所以含xy4项的系数为C×25×C=6×32×5=960.故选B.
5.答案:A
解析:完成排戏曲节目演出顺序这件事,可以有两类办法:京剧排第一,越剧、粤剧排在一起作一个元素与余下三个作全排列有A,越剧、粤剧有前后A,共有:AA种;
京剧排二三之一有C,越剧、粤剧排在一起只有三个位置并且它们有先后,有CA,余下三个有A,共有:CCAA种;
由分类加法计数原理知,所有演出顺序有:AA+CCAA=120(种).故选A.
6.答案:C
解析:第一关闯关成功的选手有80人,则第一关闯关成功的频率为0.8,
第一关闯关成功且第二关闯关也成功的选手有72人,则两关都成功的频率为0.72.
设“第一关闯关成功”为事件A,“第二关闯关成功”为事件B,
P(A)=0.8,P(AB)=0.72,某个选手第一关闯关成功,
则该选手第二关闯关成功的概率为P(B|A)==0.9.故选C.
7.答案:D
解析:A,B,C,D,E用三种颜色涂色,则有CA=60种方式,
A,B,C,D,E用四种颜色涂色,则有2CA=240种方式,
A,B,C,D,E用五种颜色涂色,则有A=120种方式,
所以一共有60+240+120=420种方式.故选D.
8.答案:C
解析:令x=0得,a0=28,故A正确;
因为(x-2)8的通项为Tk+1=Cx8-k(-2)k,所以a8=C(-2)0=1,故B正确;
令x=1,则a0+a1+a2+…+a8=(1-2)8=1,
又a0=28,所以a1+a2+…+a8=1-28,故C错误;
令x=-1,则a0-a1+a2-…+a8=(-1-2)8=38,故D正确.故选C.
9.答案:ABD
解析:选项A:若对每名教师志愿者去哪道校门无要求,
则共有34=81种不同的安排方法.判断正确;
选项B:若恰有一道门没有教师志愿者去,
则可以先把4名教师分成2组,再分配给东门、西门、北门三道校门.
则共有(CC+)A=42(种)不同的安排方法.判断正确;
选项C:若甲、乙两人都不能去北门,且每道门都有教师志愿者去,
则北门可以安排1名教师或安排2名教师.
则共有CCCA+CA=14(种)不同的安排方法.判断错误;
选项D:若学校新购入20把同一型号的额温枪,准备全部分配给三道校门使用,
每道校门至少3把,则先分配给三道校门各2把,还剩14把,
将14把额温枪排成一排,在中间13个空位中置入2个挡板,
共有C=78(种)分配方法.判断正确.
故选ABD.
10.答案:AD
解析:至少有一枚骰子的点数是3,即只有一枚骰子的点数是3,或两枚骰子的点数都是3,概率为P==,A正确;
由独立事件同时发生的概率公式得题被解出的概率为P=1-(1-)×(1-)=,B错;
如果选出的两名学生是一男一女,则两个事件同时发生,它们不是互斥事件,C错;
两位男生和两位女生随机排成一列,总排法为A=24,两位女生不相邻的排法为AA=12,概率为P==,D正确.故选AD.
11.答案:AC
解析:由X~N(2,σ2),则μ=2,
对于A,由=2,则P(2对于B,P(1对于C,由μ=2,则P(X<2)=0.5,P(X<1)=P(X<2)-P(10.24=P(X<1)>P(0对于D,由C可知,P(X<1)=0.24<0.26=P(212.答案:ACD
解析:若事件A与B互相独立,且0随机变量X服从正态分布N(0,1).可得μ=0,σ2=1,则P(|x|<)=1-2P(X≥),故B错误;
在回归分析中,对一组给定的样本数据(x1,y1),(x2,y2),…,(xn,yn)而言,残差平方和越大,则模型的拟合效果越差;反之,则模型的拟合效果越好,故C正确;
若随机变量ξ服从二项分布B(4,),则E(ξ)=1,E(2ξ+3)=2E(ξ)+3=5,故D正确.故选ACD.
13.答案:160
解析:因为二项式系数之和为64,
故有2n=64,得n=6,
二项式(2x3+)6的通项为
Tk+1=C(2x3)6-k()k=C26-kx18-4k,
令18-4k=6,得k=3,所以T4=C23x6=160x6.
即x6的系数是160.
14.答案:9
解析:因为X~B(12,0.25),所以E(X)=12×0.25=3,D(X)=12×0.25×(1-0.25)=,
又E(aX-3)=aE(X)-3=3,
即3a-3=3,解得a=2,
所以D(aX-3)=D(2X-3)=22D(X)=4×=9.
15.答案:(0,)
解析:由已知得P(η=1)=p,P(η=2)=(1-p)p,P(η=3)=(1-p)2,
则E(η)=p+2(1-p)p+3(1-p)2=p2-3p+3>,
解得p>或p<,又p∈(0,1),所以p∈(0,).
16.答案:
解析:由题意可知,随机变量X的取值范围为{0,1,2,3},
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
所以E(X)=0×+1×+2×+3×=.
由已知条件可得P(A)=P(X=1)+P(X=2)=+=.
17.解析:(1)设“当天小王的该邮箱被锁定”为事件A,
则P(A)=××=.
(2)由题意,X可能取到1,2,3,
则P(X=1)=,
P(X=2)=×=,
P(X=3)=××1=,
所以X的分布列为
X 1 2 3
P
所以E(X)=1×+2×+3×=,
D(X)=(1-)2×+(2-)2×+(3-)2×=.
18.解析:(1)∵此人连续两次命中8环的概率为(0.4)2=0.16,连续两次命中9环的概率为(0.4)2=0.16,连续两次命中10环的概率为(0.2)2=0.04.
∴此人两次命中环数相同的概率为0.16+0.16+0.04=0.36.
(2)由题意可知:ξ所有可能的取值为8,9,10,
∵P(ξ=8)=0.4×0.4=0.16;P(ξ=9)=0.4×0.4+C×0.4×0.4=0.48,P(ξ=10)=0.2×0.2+C×0.2×(1-0.2)=0.36.
∴ξ的分布列为
ξ 8 9 10
P 0.16 0.48 0.36
19.解析:(1)由题得
喜爱运动 不喜爱运动 总计
男 12 6 18
女 6 6 12
总计 18 12 30
假设是否喜爱运动与性别无关,由已知数据可求得
χ2=≈0.833 3<2.706,
因此,根据小概率值α=0.1的χ2独立性检验,没有充分的把握判断喜爱运动与性别有关.
(2)ξ的可能取值为0,1,2,3,
则P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==,P(ξ=3)==.
所以ξ的分布列为
ξ 0 1 2 3
P
20.解析:(1)两人得分之和不大于33分,即两人得分均为16分,或两人中1人16分,1人17分,
P==.
(2)=160×0.06+170×0.12+180×0.34+190×0.30+200×0.1+210×0.08=185,
又σ2≈169,σ=13,所以正式测试时,μ=195,σ=13,∴μ-σ=182.
(ⅰ)∴P(ξ>182)=1-=0.841 3,
∴0.841 3×2 000=1682.6≈1 683(人).
(ⅱ)由正态分布模型,全年级所有学生中任取1人,每分钟跳绳个数195以上的概率为0.5,即ξ~B(3,0.5),
∴P(ξ=0)=C(1-0.5)3=0.125,P(ξ=1)=C0.5·(1-0.5)2=0.375,
P(ξ=2)=C0.52·(1-0.5)=0.375,P(ξ=3)=C0.53=0.125.
∴ξ的分布列为
ξ 0 1 2 3
P 0.125 0.375 0.375 0.125
E(ξ)=3×0.5=1.5.
21.解析:(1)根据题意,两天一共销售该食品的份数为ξ的取值依次为30,31,32,33,34,35,36,
P(ξ=30)=×=,
P(ξ=31)=××2=,
P(ξ=32)=××2+×=,
P(ξ=33)=××2+××2=,
P(ξ=34)=××2+×=,
P(ξ=35)=××2=,
P(ξ=36)=×=,
所以ξ的分布列为
ξ 30 31 32 33 34 35 36
P
所以E(ξ)=30×+31×+32×+33×+34×+35×+36×=32.8.
(2)当一次性购进32份时,利润的数学期望为32×4×+(31×4-8)×+(30×4-16)×=125.6,
当一次性购进33份时,利润的数学期望为
33×4×+(32×4-8)×+(31×4-16)×+(30×4-24)×=124.68,
由125.6>124.68可知,当一次性购进32份该食品时,获得的利润更高.
22.解析:(1)根据散点图判断,y=c·edx更适宜作为描述y与x关系的回归方程类型.
理由:方程y=a+bx表示的是直线,而方程y=c·edx表示的是曲线,散点图表示的是曲线.
(2)∵y=c·edx,∴ln y=ln (c·edx)=ln edx+ln c=dx+ln c,
设w=ln y,则有w=dx+ln c,
d===0.74,ln c=-d=3.49-0.74×3.5=0.9,
∴w=0.74x+0.9,所以y关于x的回归方程为y=e0.74x+0.9.
当x=10时,y=e0.74×10+0.9=e8.3≈4 023.87,
则该志愿者在注射疫苗后的第10天的抗体含量水平值约为4 023.87 miu/mL.
(3)由表中数据可知,前三天的y值小于50,故X的可能取值为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==.
故X的分布列为
X 0 1 2 3
P
所以数学期望E(X)=0×+1×+2×+3×=.
时间:120分钟 满分:150分
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某车间加工某种机器的零件数x(单位:个)与加工这些零件所花费的时间y(单位:min)之间的对应数据如下表所示:
x/个 10 20 30 40 50
y/min 62 68 75 81 89
由表中的数据可得回归直线方程=x+54.9,则加工70个零件比加工60个零件大约多用( )
A.5.8 min B.6 min C.6.7 min D.8 min
2.已知服从正态分布N(μ,σ2)的随机变量在区间(μ-σ,μ+σ],(μ-2σ,μ+2σ]和(μ-3σ,μ+3σ]内取值的概率分别为68.26%,95.44%和99.74%.若某校高二年级1 000名学生的某次考试成绩X服从正态分布N(90,152),则此次考试成绩在区间(105,120]内的学生大约有( )
A.477人 B.136人 C.341人 D.131人
3.围棋起源于中国,据先秦典籍《世本》记载“尧造围棋,丹朱善之”,围棋至今已有四千多年历史,蕴含着中华文化的丰富内涵.在某次国际围棋比赛中,甲、乙两人进入最后决赛.比赛采取五局三胜制,即先胜三局的一方获得比赛冠军(假设没有平局),比赛结束假设每局比赛乙胜甲的概率都为,且各局比赛的胜负互不影响,则在不超过4局的比赛中甲获得冠军的概率为( )
A. B. C. D.
4.在(2+x)6(1+y)m的展开式中,令x3y的系数为800,则含xy4项的系数为( )
A.30 B.960 C.300 D.360
5.2021年某地电视台春晚的戏曲节目,准备了经典京剧、豫剧、越剧、粤剧、黄梅戏、评剧6个剧种的各一个片段.对这6个剧种的演出顺序有如下要求:京剧必须排在前三,且越剧、粤剧必须排在一起,则该戏曲节目演出顺序共有( )
A.120种 B.156种 C.188种 D.240种
6.在某电视台有一闯关节目,该节目设置有两关,闯关规则是:当第一关闯关成功后,方可进入第二关.为了调查闯关的难度,该电视台调查了参加过此节目的100名选手的闯关情况,第一关闯关成功的有80人,第一关闯关成功且第二关闯关也成功的选手有72人,以闯关成功的频率近似作为闯关成功的概率,已知某个选手第一关闯关成功,则该选手第二关闯关成功的概率为( )
A.0.72 B.0.8 C.0.9 D.0.576
7.用5种不同颜色给图中5个车站的候车牌(E,A,B,C,D)染色,要求相邻的两个车站间的候车牌不同色,染色方法有( )
A.120种 B.180种 C.360种 D.420种
8.已知(x-2)8=a0+a1x+a2x2+…+a8x8,则下列结论不正确的是( )
A.a0=28 B.a8=1
C.a1+a2+…+a8=1 D.a0-a1+a2-…+a8=38
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.某校共有东门、西门、北门三道校门.由于疫情防控需要,学校安排甲、乙、丙、丁4名教师志愿者分别去三道校门协助保安值守,下列选项正确的是( )
A.若对每名教师志愿者去哪道校门无要求,则共有81种不同的安排方法
B.若恰有一道门没有教师志愿者去,则共有42种不同的安排方法
C.若甲、乙两人都不能去北门,且每道门都有教师志愿者去,则共有44种不同的安排方法
D.若学校新购入20把同一型号的额温枪,准备全部分配给三道校门使用,每道校门至少3把,则共有78种分配方法
10.下列说法正确的是( )
A.抛掷两枚质地均匀的骰子,至少有一枚骰子的点数是3的概率为
B.甲乙两人独立地解题,已知各人能解出的概率分别是,,则题被解出的概率是
C.某小组由5名学生组成,其中3名男生,2名女生,现从中任选两名学生参加演讲比赛,至少有一名男生与至少有一名女生是互斥事件
D.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是
11.已知随机变量X~N(2,σ2),且P(1
A.若事件A与B互相独立,且0
C.在回归分析中,对一组给定的样本数据(x1,y1),(x2,y2),…,(xn,yn)而言,若残差平方和越大,则模型的拟合效果越差;反之,则模型的拟合效果越好
D.若随机变量ξ服从二项分布B(4,),则E(2ξ+3)=5
三、填空题:本题共4小题,每小题5分,共20分.
13.在二项式(2x3+)n的展开式中,所有的二项式系数之和为64,则该展开式中的x6的系数是________.
14.已知随机变量X服从二项分布B(12,0.25),且E(aX-3)=3(a∈R),则D(aX-3)=________.
15.某商场在儿童节举行回馈顾客活动,凡在商场消费满100元者即可参加射击赢玩具活动,具体规则如下:每人最多可射击3次,一旦击中,则可获奖且不再继续射击,否则一直射击到3次为止.设甲每次击中的概率为p(p≠0),射击次数为Y,若Y的数学期望E(Y)>,则p的取值范围是________.
16.在是否接种疫苗的调查中调查了7人,7人中有4人未接种疫苗,3人接种了疫苗,从这7人中随机抽取3人进行身体检查,用X表示抽取的3人中未接种疫苗的人数,则随机变量X的数学期望为________,设A为事件“抽取的3人中,既有接种疫苗的人,也有未接种疫苗的人”,则事件A发生的概率为________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)某网站规定:一个邮箱在一天内出现3次密码尝试错误,该邮箱将被锁定24小时.小王发现自己忘记了邮箱密码,但是可以确定该邮箱的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该邮箱被锁定.
(1)求当天小王的该邮箱被锁定的概率;
(2)设当天小王尝试该邮箱的密码次数为X,求X的分布列及E(X),D(X)的值.
18.(12分)为迎接2022年8月8日至8月18日在六盘水市举行的贵州省第十一届运动会,运动员们正艰苦训练,积极备战.某运动员射击一次所得环数X的分布列如下:
X 8 9 10
P 0.4 0.4 0.2
现进行两次射击,且两次射击互不影响,以该运动员两次射击中最高环数作为他的成绩,记为ξ.
(1)求此人两次命中环数相同的概率;
(2)求ξ的分布列和数学期望E(ξ).
19.(12分)在“双减”政策背景之下,某校就推进学校、家庭、社会体育教育的“一体化”,实现“教会、勤练、常赛”的核心任务.学校组织人员对在校学生“是否喜爱运动”做了一次随机调查.共随机调查了18名男生和12名女生,调查发现,男、女生中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下2×2列联表:根据小概率值α=0.1的χ2独立性检验,能否据此推断性别与喜爱运动有关?
喜欢运动 不喜欢运动 总计
男
女
总计
(2)从被调查的女生中抽取3人,若其中喜爱运动的人数为ξ,求ξ的分布列.
附参考公式及参考数据:
α=P(χ2≥k) 0.40 0.25 0.10 0.010
k 0.708 1.323 2.706 6.635
χ2=,其中n=a+b+c+d.
20.(12分)当前,以“立德树人”为目标的课程改革正在有序推进. 高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施. 某地区2018年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分为50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分. 某学校在初三上学期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数 [155,165) [165,175) [175,185) [185,+∞)
得分 16 17 19 20
(1)现从样本的100名学生中,任意选取2人,求两人得分之和不大于33分的概率;
(2)若该校初三年级所有学生的跳绳个数X服从正态分布N(μ,σ2),用样本数据的平均值和方差估计总体的期望和方差,已知样本方差s2≈169 (各组数据用中点值代替). 根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
(ⅰ)预估全年级恰好有2 000名学生时,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
(ⅱ)若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195个以上的人数为ξ,求随机变量ξ的分布列和期望.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ-σ
销售量(份) 15 16 17 18
天数 20 30 40 10
(1)根据该食品在本地区100天的销售量统计表,记两天一共销售该食品的份数为ξ,求ξ的分布列与数学期望;(视样本频率为概率)
(2)以两天内该食品所获得的利润的数学期望为决策依据,若该商店计划一次性购进32份或33份该食品,试判断哪一种获得的利润更高.
22.(12分)新冠肺炎疫情发生以来,我国某科研机构开展应急科研攻关,研制了一种新型冠状病毒疫苗,并已进入二期临床试验.根据普遍规律,志愿者接种疫苗后体内会产生抗体,人体中检测到抗体,说明有抵御病毒的能力.通过检测,用x表示注射疫苗后的天数,y表示人体中抗体含量水平(单位:miu/mL,即:百万国际单位/毫升),现测得某志愿者的相关数据如下表所示.
天数x 1 2 3 4 5 6
抗体含量水平y 5 10 26 50 96 195
根据以上数据,绘制了散点图.
(1)根据散点图判断,y=c·edx与y=a+bx(a,b,c,d均为大于0的实数),哪一个更适宜作为描述y与x关系的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果求出y关于x的回归方程,并预测该志愿者在注射疫苗后的第10天的抗体含量水平值;
(3)从这位志愿者的前6天的检测数据中随机抽取3天的数据作进一步的分析,求其中的y值小于50的天数X的分布列及数学期望.
参考数据:其中w=ln y.
(xi-)2 (wi-)2 (wi-)(xi-) (xi-)(yi-) e8.3
3.50 63.67 3.49 17.50 9.49 12.95 519.01 4 023.87
参考公式:==,=-.
参考答案与解析
1.答案:C
解析:由表中的数据,得==30,
==75,
将,代入=x+54.9,得=0.67,
所以加工70个零件比加工60个零件大约多用70+54.9-(60+54.9)=10=6.7 min.故选C.
2.答案:B
解析:根据题意,P(105
=
=0.135 9,
则1 000×0.135 9=135.9≈136,
故此次考试成绩在区间(105,120]内的学生大约有136人.
故选B.
3.答案:A
解析:在不超过4局的比赛中甲获得冠军包含两种情况,且两种情况互斥:
①甲前三局全胜,概率为P1=()3=;
②前三局甲两胜一负,第四局甲胜,概率为
P2=C()2()()=.
∴在不超过4局的比赛中甲获得冠军的概率为
P=P1+P2=+=.故选A.
4.答案:B
解析:(2+x)6展开式中x3的系数为C×23,(1+y)m展开式中y的系数为C,
所以x3y的系数为C×23×C,
所以C×23×C=800,即160m=800,解得m=5,
所以(2+x)6展开式中x的系数为C×25,(1+y)5展开式中y4的系数为C,
所以含xy4项的系数为C×25×C=6×32×5=960.故选B.
5.答案:A
解析:完成排戏曲节目演出顺序这件事,可以有两类办法:京剧排第一,越剧、粤剧排在一起作一个元素与余下三个作全排列有A,越剧、粤剧有前后A,共有:AA种;
京剧排二三之一有C,越剧、粤剧排在一起只有三个位置并且它们有先后,有CA,余下三个有A,共有:CCAA种;
由分类加法计数原理知,所有演出顺序有:AA+CCAA=120(种).故选A.
6.答案:C
解析:第一关闯关成功的选手有80人,则第一关闯关成功的频率为0.8,
第一关闯关成功且第二关闯关也成功的选手有72人,则两关都成功的频率为0.72.
设“第一关闯关成功”为事件A,“第二关闯关成功”为事件B,
P(A)=0.8,P(AB)=0.72,某个选手第一关闯关成功,
则该选手第二关闯关成功的概率为P(B|A)==0.9.故选C.
7.答案:D
解析:A,B,C,D,E用三种颜色涂色,则有CA=60种方式,
A,B,C,D,E用四种颜色涂色,则有2CA=240种方式,
A,B,C,D,E用五种颜色涂色,则有A=120种方式,
所以一共有60+240+120=420种方式.故选D.
8.答案:C
解析:令x=0得,a0=28,故A正确;
因为(x-2)8的通项为Tk+1=Cx8-k(-2)k,所以a8=C(-2)0=1,故B正确;
令x=1,则a0+a1+a2+…+a8=(1-2)8=1,
又a0=28,所以a1+a2+…+a8=1-28,故C错误;
令x=-1,则a0-a1+a2-…+a8=(-1-2)8=38,故D正确.故选C.
9.答案:ABD
解析:选项A:若对每名教师志愿者去哪道校门无要求,
则共有34=81种不同的安排方法.判断正确;
选项B:若恰有一道门没有教师志愿者去,
则可以先把4名教师分成2组,再分配给东门、西门、北门三道校门.
则共有(CC+)A=42(种)不同的安排方法.判断正确;
选项C:若甲、乙两人都不能去北门,且每道门都有教师志愿者去,
则北门可以安排1名教师或安排2名教师.
则共有CCCA+CA=14(种)不同的安排方法.判断错误;
选项D:若学校新购入20把同一型号的额温枪,准备全部分配给三道校门使用,
每道校门至少3把,则先分配给三道校门各2把,还剩14把,
将14把额温枪排成一排,在中间13个空位中置入2个挡板,
共有C=78(种)分配方法.判断正确.
故选ABD.
10.答案:AD
解析:至少有一枚骰子的点数是3,即只有一枚骰子的点数是3,或两枚骰子的点数都是3,概率为P==,A正确;
由独立事件同时发生的概率公式得题被解出的概率为P=1-(1-)×(1-)=,B错;
如果选出的两名学生是一男一女,则两个事件同时发生,它们不是互斥事件,C错;
两位男生和两位女生随机排成一列,总排法为A=24,两位女生不相邻的排法为AA=12,概率为P==,D正确.故选AD.
11.答案:AC
解析:由X~N(2,σ2),则μ=2,
对于A,由=2,则P(2
解析:若事件A与B互相独立,且0
在回归分析中,对一组给定的样本数据(x1,y1),(x2,y2),…,(xn,yn)而言,残差平方和越大,则模型的拟合效果越差;反之,则模型的拟合效果越好,故C正确;
若随机变量ξ服从二项分布B(4,),则E(ξ)=1,E(2ξ+3)=2E(ξ)+3=5,故D正确.故选ACD.
13.答案:160
解析:因为二项式系数之和为64,
故有2n=64,得n=6,
二项式(2x3+)6的通项为
Tk+1=C(2x3)6-k()k=C26-kx18-4k,
令18-4k=6,得k=3,所以T4=C23x6=160x6.
即x6的系数是160.
14.答案:9
解析:因为X~B(12,0.25),所以E(X)=12×0.25=3,D(X)=12×0.25×(1-0.25)=,
又E(aX-3)=aE(X)-3=3,
即3a-3=3,解得a=2,
所以D(aX-3)=D(2X-3)=22D(X)=4×=9.
15.答案:(0,)
解析:由已知得P(η=1)=p,P(η=2)=(1-p)p,P(η=3)=(1-p)2,
则E(η)=p+2(1-p)p+3(1-p)2=p2-3p+3>,
解得p>或p<,又p∈(0,1),所以p∈(0,).
16.答案:
解析:由题意可知,随机变量X的取值范围为{0,1,2,3},
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
所以E(X)=0×+1×+2×+3×=.
由已知条件可得P(A)=P(X=1)+P(X=2)=+=.
17.解析:(1)设“当天小王的该邮箱被锁定”为事件A,
则P(A)=××=.
(2)由题意,X可能取到1,2,3,
则P(X=1)=,
P(X=2)=×=,
P(X=3)=××1=,
所以X的分布列为
X 1 2 3
P
所以E(X)=1×+2×+3×=,
D(X)=(1-)2×+(2-)2×+(3-)2×=.
18.解析:(1)∵此人连续两次命中8环的概率为(0.4)2=0.16,连续两次命中9环的概率为(0.4)2=0.16,连续两次命中10环的概率为(0.2)2=0.04.
∴此人两次命中环数相同的概率为0.16+0.16+0.04=0.36.
(2)由题意可知:ξ所有可能的取值为8,9,10,
∵P(ξ=8)=0.4×0.4=0.16;P(ξ=9)=0.4×0.4+C×0.4×0.4=0.48,P(ξ=10)=0.2×0.2+C×0.2×(1-0.2)=0.36.
∴ξ的分布列为
ξ 8 9 10
P 0.16 0.48 0.36
19.解析:(1)由题得
喜爱运动 不喜爱运动 总计
男 12 6 18
女 6 6 12
总计 18 12 30
假设是否喜爱运动与性别无关,由已知数据可求得
χ2=≈0.833 3<2.706,
因此,根据小概率值α=0.1的χ2独立性检验,没有充分的把握判断喜爱运动与性别有关.
(2)ξ的可能取值为0,1,2,3,
则P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==,P(ξ=3)==.
所以ξ的分布列为
ξ 0 1 2 3
P
20.解析:(1)两人得分之和不大于33分,即两人得分均为16分,或两人中1人16分,1人17分,
P==.
(2)=160×0.06+170×0.12+180×0.34+190×0.30+200×0.1+210×0.08=185,
又σ2≈169,σ=13,所以正式测试时,μ=195,σ=13,∴μ-σ=182.
(ⅰ)∴P(ξ>182)=1-=0.841 3,
∴0.841 3×2 000=1682.6≈1 683(人).
(ⅱ)由正态分布模型,全年级所有学生中任取1人,每分钟跳绳个数195以上的概率为0.5,即ξ~B(3,0.5),
∴P(ξ=0)=C(1-0.5)3=0.125,P(ξ=1)=C0.5·(1-0.5)2=0.375,
P(ξ=2)=C0.52·(1-0.5)=0.375,P(ξ=3)=C0.53=0.125.
∴ξ的分布列为
ξ 0 1 2 3
P 0.125 0.375 0.375 0.125
E(ξ)=3×0.5=1.5.
21.解析:(1)根据题意,两天一共销售该食品的份数为ξ的取值依次为30,31,32,33,34,35,36,
P(ξ=30)=×=,
P(ξ=31)=××2=,
P(ξ=32)=××2+×=,
P(ξ=33)=××2+××2=,
P(ξ=34)=××2+×=,
P(ξ=35)=××2=,
P(ξ=36)=×=,
所以ξ的分布列为
ξ 30 31 32 33 34 35 36
P
所以E(ξ)=30×+31×+32×+33×+34×+35×+36×=32.8.
(2)当一次性购进32份时,利润的数学期望为32×4×+(31×4-8)×+(30×4-16)×=125.6,
当一次性购进33份时,利润的数学期望为
33×4×+(32×4-8)×+(31×4-16)×+(30×4-24)×=124.68,
由125.6>124.68可知,当一次性购进32份该食品时,获得的利润更高.
22.解析:(1)根据散点图判断,y=c·edx更适宜作为描述y与x关系的回归方程类型.
理由:方程y=a+bx表示的是直线,而方程y=c·edx表示的是曲线,散点图表示的是曲线.
(2)∵y=c·edx,∴ln y=ln (c·edx)=ln edx+ln c=dx+ln c,
设w=ln y,则有w=dx+ln c,
d===0.74,ln c=-d=3.49-0.74×3.5=0.9,
∴w=0.74x+0.9,所以y关于x的回归方程为y=e0.74x+0.9.
当x=10时,y=e0.74×10+0.9=e8.3≈4 023.87,
则该志愿者在注射疫苗后的第10天的抗体含量水平值约为4 023.87 miu/mL.
(3)由表中数据可知,前三天的y值小于50,故X的可能取值为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==.
故X的分布列为
X 0 1 2 3
P
所以数学期望E(X)=0×+1×+2×+3×=.
