人教版高中数学必修第一册4.2实际问题的函数建模 课件(共27张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册4.2实际问题的函数建模 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 494.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 10:40:45 | ||
图片预览








文档简介
(共27张PPT)
第四章 函数应用
§2 实际问题的函数建模
1.了解什么是函数模型,知道函数的一些基本模型,知道数学建模的意义;
2.通过对函数模型应用实例的学习,学会对收集到的相关数据进行拟合,并建立适当的数学模型;
3.掌握建立函数模型的一般方法,学会运用常见的函数模型来解一些简单的实际问题.
问题导学
题型探究
达标检测
学习目标
知识点一 实际问题的函数刻画
思考 世界上很多事物间的联系可以用函数刻画,在试图用函数刻画两个变量的联系时,需要关注哪些要点?
答案 先确定两个变量是谁;
再看两个变量之间的对应关系是否满足函数定义;
如果满足,就要考虑建立函数关系式.
一般地,设自变量为x,函数为y,并用x表示各相关量,然后根据问题的已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系式,将实际问题转化为数学问题,实现问题的数学化,即所谓建立数学模型.
答案
问题导学 新知探究 点点落实
答案
知识点二 用函数模型解决实际问题
思考 函数模型是应用最广泛的数学模型之一,一旦确定是函数模型,怎样研究它?
答案 先确定函数关系式,再根据解决实际问题的需要针对性研究函数性质,如定义域、最值、单调性等,使实际问题得到解决.
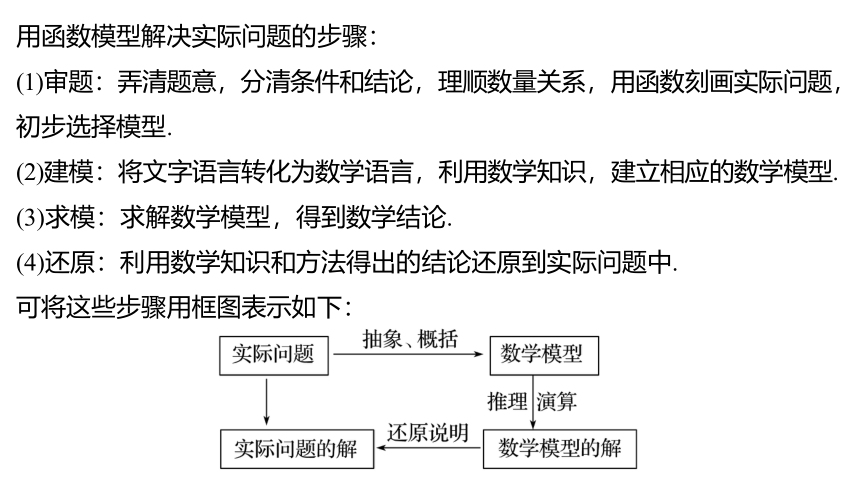
用函数模型解决实际问题的步骤:
(1)审题:弄清题意,分清条件和结论,理顺数量关系,用函数刻画实际问题,初步选择模型.
(2)建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型.
(3)求模:求解数学模型,得到数学结论.
(4)还原:利用数学知识和方法得出的结论还原到实际问题中.
可将这些步骤用框图表示如下:
答案
知识点三 数据拟合
思考 自由落体速度公式v=gt是一种函数模型.类比这个公式的发现过程,简述什么是数据拟合?
答案 函数模型来源于现实(伽利略斜塔抛球),通过收集数据(打点计时器测量),画散点图分析数据(增长速度、单位时间内的增长量等),寻找或选择函数(假说)来作为函数模型,再检验这个函数模型是否符合实际,这就是数据拟合.
数据拟合:
(1)定义:通过一些数据寻求事物规律,往往是通过绘出这些数据在直角坐标系中的点,观察这些点的整体特征,看它们接近我们熟悉的哪一种函数图像,选定函数形式后,将一些数据代入这个函数的一般表达式,求出具体的函数表达式,再做必要的检验,基本符合实际,就可以确定这个函数基本反映了事物规律.这种方法称为数据拟合.
(2)数据拟合的步骤:
①以所给数据作为点的坐标,在平面直角坐标系中绘出各点;
②依据点的整体特征,猜测这些点所满足的函数形式,设其一般形式;
③取特殊数据代入,求出函数的具体解析式;
④做必要的检验.
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 利用已知函数模型求解实际问题
例1 某列火车从北京西站开往石家庄,全程277 km.火车出发10 min开出13 km后,以120 km/h的速度匀速行驶.试写出火车行驶的总路程S与匀速行驶的时间t之间的关系,并求火车离开北京2 h内行驶的路程.
因为火车匀速行驶时间t h所行驶路程为120t,
所以,火车运行总路程S与匀速行驶时间t之间的关系是S=13+120t(0≤t≤ ).
反思与感悟
(1)审题是解决问题的起点,需弄清楚题中有几层意思,每层意思是什么,要解决什么问题及其相关的因素有哪些等.即从中收集有用信息,捕捉关键词语,从文字语言叙述中理解题意,不能漏掉任何一个条件.
(2)建模需设出有关符号、字母等来表示题目中的有关量,根据题目中所给出的等量关系或结合实际生产、生活中的等量关系,建立函数关系.
(3)对于实际问题,所有的取值都是有实际意义的,即要注重函数的定义域,这往往是解决问题时容易遗漏的.
(4)实际问题中出现不同的度量单位时,要将其化成统一的度量单位.
解析答案
跟踪训练1 商店出售茶壶与茶杯,茶壶每个定价20元,茶杯每个5元,该商店推出两种优惠办法:①买一个茶壶送一个茶杯,②按购买总价的92%付款.某顾客购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款为y(元),试分别建立两种优惠办法中y与x的函数关系式,并指出如果该顾客需要购买茶杯40个,应选择哪种优惠办法?
解 由优惠办法①得函数关系式为y1=20×4+5(x-4)=5x+60(x≥4,x∈N+).
由优惠办法②得函数关系式为y2=(20×4+5x)×92%=4.6x+73.6(x≥4,x∈N+).
当该顾客购买茶杯40个时,采用优惠办法①应付款y1=5×40+60=260元;
采用优惠办法②应付款y2=4.6×40+73.6=257.6元,
由于y2解析答案
类型二 自建确定性函数模型解决实际问题
例2 某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y= -48x+8 000,已知此生产线年产量最大为210吨.若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
解 设可获得总利润为R(x)万元,
∵R(x)在[0,210]上是增函数,
∴年产量为210吨时,可获得最大利润1 660万元.
反思与感悟
反思与感悟
自建模型时主要抓住四个关键:“求什么,设什么,列什么,限制什么”.
求什么就是弄清楚要解决什么问题,完成什么任务.
设什么就是弄清楚这个问题有哪些因素,谁是核心因素,通常设核心因素为自变量.
列什么就是把问题已知条件用所设变量表示出来,可以是方程、函数、不等式等.
限制什么主要是指自变量所应满足的限制条件,在实际问题中,除了要使函数式有意义外,还要考虑变量的实际含义,如人不能是半个等.
解析答案
跟踪训练2 有甲、乙两种商品,经营销售这两种商品所获得的利润依次为Q1万元和Q2万元,它们与投入的资金x万元的关系是Q1= x,Q2= .
现有3万元资金投入使用,则对甲、乙两种商品如何投资才能获得最大利润?
解 设对甲种商品投资x万元,
则对乙种商品投资(3-x)万元,总利润为y万元.
所以3-x=2.25(万元).
由此可知,为获得最大利润,对甲、乙两种商品的资金投入分别为0.75万元和2.25万元,总共获得利润为1.05万元.
类型三 拟合函数模型
例3 人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:y=y0ert,其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率.下表是1950~1959年我国的人口数据资料:
年份 1950 1951 1952 1953 1954
人数/万人 55 196 56 300 57 482 58 796 60 266
年份 1955 1956 1957 1958 1959
人数/万人 61 456 62 828 64 563 65 994 67 207
解析答案
(1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.000 1),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
解 设1951~1959年的人口增长率分别为r1,r2,…,r9.
由55 196(1+r1) = 56 300,可得1951年的人口增长率r1≈0.020 0.
同理可得,r2≈0.021 0,r3≈0.022 9,r4≈0.025 0,r5≈0.019 7,r6≈0.022 3,r7≈0.027 6,r8≈0.022 2,r9≈0.018 4.于是,1951~1959年期间,我国人口的年均增长率为r=(r1+r2+…+r9)÷9≈0.022 1.
令y0=55 196,则我国在1950~1959年期间
的人口增长模型为y=55 196e0.022 1t,t∈N.
根据表中的数据作出散点图,
并作出函数y=55 196e0.022 1t(t∈N)的图像.
由图可以看出,所得模型与1950~1959年的实际人口数据基本吻合.
解析答案
反思与感悟
(2)如果按表中的增长趋势,大约在哪一年我国的人口达到13亿?
解 将y=130 000代入y=55 196e0.022 1t,
由计算器可得t≈38.76.
所以,如果按表的增长趋势,那么大约在1950年后的第39年(即1989年)我国的人口就已达到13亿.
反思与感悟
(1)已给出函数模型的实际应用题,关键是考虑该题考查的是何种函数,并要注意定义域,然后结合所给模型,列出函数关系式,最后结合其实际意义作出解答.
(2)判断所得到的数学模型是否拟合,必须使所有数据基本接近数学模型,对于一般的应用问题,不会让数学模型完全符合,只是基本符合,对此,无最优解,只有满意解.
(3)由于函数模型的局限性、函数模型往往只在某个范围内拟合效果较好.
跟踪训练3 已知1650年世界人口为5亿,当时人口的年增长率为0.3%;1970年世界人口为36亿,当时人口的年增长率为2.1%.
(1)用马尔萨斯人口模型计算,什么时候世界人口是1650年的2倍?什么时候世界人口是1970年的2倍?
解 已知人口模型为y=y0ert,其中y0表示t=0时的人口数,r表示人口的年增长率.
若按1650年世界人口5亿,年增长率为0.3%估计,有y=5e0.003t.
当y=10时,解得t≈231.
同理可知,2003年世界人口数约为1970年的2倍.
(2)实际上,1850年以前世界人口就超过了10亿;而2003年世界人口还没有达到72亿.你对同样的模型得出的两个结果有何看法?
解 由此看出,此模型不太适宜估计时间跨度非常大的人口增长情况.
所以,1881年世界人口约为1650年的2倍.
解析答案
返回
1
2
3
达标检测
4
1.从2013年起,在20年内某海滨城市力争使全市工农业生产总产值翻两番,如果每年的增长率是8%,则达到翻两番目标的最少年数为( )
A.17 B.18
C.19 D.20
5
C
答案
2.一辆汽车在某段路程中的行驶路程s关于时间t变化的图像如图所示,那么图像所对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
1
2
3
4
5
A
答案
3.若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是( )
A. B.y=(0.957 6)100x
C.y=( )x D.
1
2
3
4
5
A
答案
4.某种植物生长发育的数量y与时间x的关系如下表:
下面的函数关系式中,拟合效果最好的是( )
A.y=2x-1
B.y=x2-1
C.y=2x-1
D.y=1.5x2-2.5x+2
1
2
3
4
5
x 1 2 3 …
y 1 3 8 …
D
答案
5.某同学最近5年内的学习费用y千元与时间x年的关系如图所示,可选择的模拟函数模型是( )
A.y=ax+b
B.y=ax2+bx+c
C.y=aex+b
D.y=aln x+b
1
2
3
4
5
B
答案
返回
规律与方法
解函数应用问题的步骤(四步八字)
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型;
(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;
(3)求模:求解数学模型,得出数学结论;
(4)还原:将数学问题还原为实际问题的意义.
本课结束
第四章 函数应用
§2 实际问题的函数建模
1.了解什么是函数模型,知道函数的一些基本模型,知道数学建模的意义;
2.通过对函数模型应用实例的学习,学会对收集到的相关数据进行拟合,并建立适当的数学模型;
3.掌握建立函数模型的一般方法,学会运用常见的函数模型来解一些简单的实际问题.
问题导学
题型探究
达标检测
学习目标
知识点一 实际问题的函数刻画
思考 世界上很多事物间的联系可以用函数刻画,在试图用函数刻画两个变量的联系时,需要关注哪些要点?
答案 先确定两个变量是谁;
再看两个变量之间的对应关系是否满足函数定义;
如果满足,就要考虑建立函数关系式.
一般地,设自变量为x,函数为y,并用x表示各相关量,然后根据问题的已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系式,将实际问题转化为数学问题,实现问题的数学化,即所谓建立数学模型.
答案
问题导学 新知探究 点点落实
答案
知识点二 用函数模型解决实际问题
思考 函数模型是应用最广泛的数学模型之一,一旦确定是函数模型,怎样研究它?
答案 先确定函数关系式,再根据解决实际问题的需要针对性研究函数性质,如定义域、最值、单调性等,使实际问题得到解决.
用函数模型解决实际问题的步骤:
(1)审题:弄清题意,分清条件和结论,理顺数量关系,用函数刻画实际问题,初步选择模型.
(2)建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型.
(3)求模:求解数学模型,得到数学结论.
(4)还原:利用数学知识和方法得出的结论还原到实际问题中.
可将这些步骤用框图表示如下:
答案
知识点三 数据拟合
思考 自由落体速度公式v=gt是一种函数模型.类比这个公式的发现过程,简述什么是数据拟合?
答案 函数模型来源于现实(伽利略斜塔抛球),通过收集数据(打点计时器测量),画散点图分析数据(增长速度、单位时间内的增长量等),寻找或选择函数(假说)来作为函数模型,再检验这个函数模型是否符合实际,这就是数据拟合.
数据拟合:
(1)定义:通过一些数据寻求事物规律,往往是通过绘出这些数据在直角坐标系中的点,观察这些点的整体特征,看它们接近我们熟悉的哪一种函数图像,选定函数形式后,将一些数据代入这个函数的一般表达式,求出具体的函数表达式,再做必要的检验,基本符合实际,就可以确定这个函数基本反映了事物规律.这种方法称为数据拟合.
(2)数据拟合的步骤:
①以所给数据作为点的坐标,在平面直角坐标系中绘出各点;
②依据点的整体特征,猜测这些点所满足的函数形式,设其一般形式;
③取特殊数据代入,求出函数的具体解析式;
④做必要的检验.
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 利用已知函数模型求解实际问题
例1 某列火车从北京西站开往石家庄,全程277 km.火车出发10 min开出13 km后,以120 km/h的速度匀速行驶.试写出火车行驶的总路程S与匀速行驶的时间t之间的关系,并求火车离开北京2 h内行驶的路程.
因为火车匀速行驶时间t h所行驶路程为120t,
所以,火车运行总路程S与匀速行驶时间t之间的关系是S=13+120t(0≤t≤ ).
反思与感悟
(1)审题是解决问题的起点,需弄清楚题中有几层意思,每层意思是什么,要解决什么问题及其相关的因素有哪些等.即从中收集有用信息,捕捉关键词语,从文字语言叙述中理解题意,不能漏掉任何一个条件.
(2)建模需设出有关符号、字母等来表示题目中的有关量,根据题目中所给出的等量关系或结合实际生产、生活中的等量关系,建立函数关系.
(3)对于实际问题,所有的取值都是有实际意义的,即要注重函数的定义域,这往往是解决问题时容易遗漏的.
(4)实际问题中出现不同的度量单位时,要将其化成统一的度量单位.
解析答案
跟踪训练1 商店出售茶壶与茶杯,茶壶每个定价20元,茶杯每个5元,该商店推出两种优惠办法:①买一个茶壶送一个茶杯,②按购买总价的92%付款.某顾客购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款为y(元),试分别建立两种优惠办法中y与x的函数关系式,并指出如果该顾客需要购买茶杯40个,应选择哪种优惠办法?
解 由优惠办法①得函数关系式为y1=20×4+5(x-4)=5x+60(x≥4,x∈N+).
由优惠办法②得函数关系式为y2=(20×4+5x)×92%=4.6x+73.6(x≥4,x∈N+).
当该顾客购买茶杯40个时,采用优惠办法①应付款y1=5×40+60=260元;
采用优惠办法②应付款y2=4.6×40+73.6=257.6元,
由于y2
类型二 自建确定性函数模型解决实际问题
例2 某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y= -48x+8 000,已知此生产线年产量最大为210吨.若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
解 设可获得总利润为R(x)万元,
∵R(x)在[0,210]上是增函数,
∴年产量为210吨时,可获得最大利润1 660万元.
反思与感悟
反思与感悟
自建模型时主要抓住四个关键:“求什么,设什么,列什么,限制什么”.
求什么就是弄清楚要解决什么问题,完成什么任务.
设什么就是弄清楚这个问题有哪些因素,谁是核心因素,通常设核心因素为自变量.
列什么就是把问题已知条件用所设变量表示出来,可以是方程、函数、不等式等.
限制什么主要是指自变量所应满足的限制条件,在实际问题中,除了要使函数式有意义外,还要考虑变量的实际含义,如人不能是半个等.
解析答案
跟踪训练2 有甲、乙两种商品,经营销售这两种商品所获得的利润依次为Q1万元和Q2万元,它们与投入的资金x万元的关系是Q1= x,Q2= .
现有3万元资金投入使用,则对甲、乙两种商品如何投资才能获得最大利润?
解 设对甲种商品投资x万元,
则对乙种商品投资(3-x)万元,总利润为y万元.
所以3-x=2.25(万元).
由此可知,为获得最大利润,对甲、乙两种商品的资金投入分别为0.75万元和2.25万元,总共获得利润为1.05万元.
类型三 拟合函数模型
例3 人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为有效控制人口增长提供依据.早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:y=y0ert,其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率.下表是1950~1959年我国的人口数据资料:
年份 1950 1951 1952 1953 1954
人数/万人 55 196 56 300 57 482 58 796 60 266
年份 1955 1956 1957 1958 1959
人数/万人 61 456 62 828 64 563 65 994 67 207
解析答案
(1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.000 1),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
解 设1951~1959年的人口增长率分别为r1,r2,…,r9.
由55 196(1+r1) = 56 300,可得1951年的人口增长率r1≈0.020 0.
同理可得,r2≈0.021 0,r3≈0.022 9,r4≈0.025 0,r5≈0.019 7,r6≈0.022 3,r7≈0.027 6,r8≈0.022 2,r9≈0.018 4.于是,1951~1959年期间,我国人口的年均增长率为r=(r1+r2+…+r9)÷9≈0.022 1.
令y0=55 196,则我国在1950~1959年期间
的人口增长模型为y=55 196e0.022 1t,t∈N.
根据表中的数据作出散点图,
并作出函数y=55 196e0.022 1t(t∈N)的图像.
由图可以看出,所得模型与1950~1959年的实际人口数据基本吻合.
解析答案
反思与感悟
(2)如果按表中的增长趋势,大约在哪一年我国的人口达到13亿?
解 将y=130 000代入y=55 196e0.022 1t,
由计算器可得t≈38.76.
所以,如果按表的增长趋势,那么大约在1950年后的第39年(即1989年)我国的人口就已达到13亿.
反思与感悟
(1)已给出函数模型的实际应用题,关键是考虑该题考查的是何种函数,并要注意定义域,然后结合所给模型,列出函数关系式,最后结合其实际意义作出解答.
(2)判断所得到的数学模型是否拟合,必须使所有数据基本接近数学模型,对于一般的应用问题,不会让数学模型完全符合,只是基本符合,对此,无最优解,只有满意解.
(3)由于函数模型的局限性、函数模型往往只在某个范围内拟合效果较好.
跟踪训练3 已知1650年世界人口为5亿,当时人口的年增长率为0.3%;1970年世界人口为36亿,当时人口的年增长率为2.1%.
(1)用马尔萨斯人口模型计算,什么时候世界人口是1650年的2倍?什么时候世界人口是1970年的2倍?
解 已知人口模型为y=y0ert,其中y0表示t=0时的人口数,r表示人口的年增长率.
若按1650年世界人口5亿,年增长率为0.3%估计,有y=5e0.003t.
当y=10时,解得t≈231.
同理可知,2003年世界人口数约为1970年的2倍.
(2)实际上,1850年以前世界人口就超过了10亿;而2003年世界人口还没有达到72亿.你对同样的模型得出的两个结果有何看法?
解 由此看出,此模型不太适宜估计时间跨度非常大的人口增长情况.
所以,1881年世界人口约为1650年的2倍.
解析答案
返回
1
2
3
达标检测
4
1.从2013年起,在20年内某海滨城市力争使全市工农业生产总产值翻两番,如果每年的增长率是8%,则达到翻两番目标的最少年数为( )
A.17 B.18
C.19 D.20
5
C
答案
2.一辆汽车在某段路程中的行驶路程s关于时间t变化的图像如图所示,那么图像所对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
1
2
3
4
5
A
答案
3.若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是( )
A. B.y=(0.957 6)100x
C.y=( )x D.
1
2
3
4
5
A
答案
4.某种植物生长发育的数量y与时间x的关系如下表:
下面的函数关系式中,拟合效果最好的是( )
A.y=2x-1
B.y=x2-1
C.y=2x-1
D.y=1.5x2-2.5x+2
1
2
3
4
5
x 1 2 3 …
y 1 3 8 …
D
答案
5.某同学最近5年内的学习费用y千元与时间x年的关系如图所示,可选择的模拟函数模型是( )
A.y=ax+b
B.y=ax2+bx+c
C.y=aex+b
D.y=aln x+b
1
2
3
4
5
B
答案
返回
规律与方法
解函数应用问题的步骤(四步八字)
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型;
(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;
(3)求模:求解数学模型,得出数学结论;
(4)还原:将数学问题还原为实际问题的意义.
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
