等式的性质(1)[上学期]
文档属性
| 名称 | 等式的性质(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 443.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-08 19:17:00 | ||
图片预览



文档简介
课件9张PPT。2.1.2 等式的性质复习题:
(1)x = 3 是下列哪个方程的解? ( )
A、3x + 9 = 0 B、x = 10 – 4x
C、x(x – 2)= 3 D、2x – 7 = 12
(2)方程 的解是 ( )
A、- 3 B、 C、12 D、- 12
(3)已知x – 5 与2x – 4 的值互为相反数,列出关于x 的方程。
(4)某班开展为贫困山区学校捐书活动,捐的书比平均每人捐 3 本多 21 本,比平均每人捐4本少 27 本,求这个班有多少名学生?如果设这个班有x 名学生,请列出关于x 的方程。问题:你能用估算的方法求下列方程的解吗?
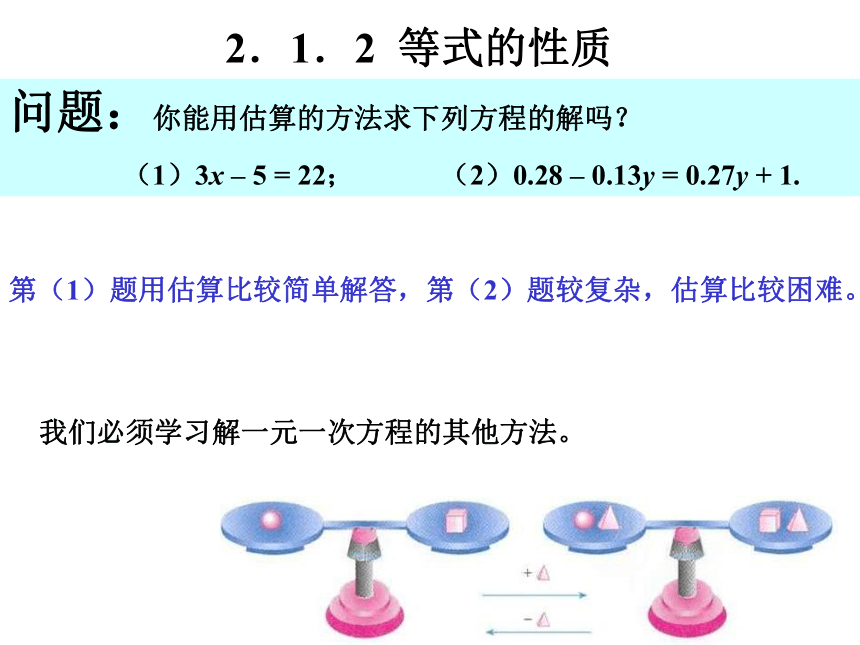
(1)3x – 5 = 22; (2)0.28 – 0.13y = 0.27y + 1.第(1)题用估算比较简单解答,第(2)题较复杂,估算比较困难。我们必须学习解一元一次方程的其他方法。2.1.2 等式的性质探求新知请同学们仔细观察课本第71页图2.1--2归纳:等式就像平衡的天平,它具有与上面的事实同样的性质。比如“8 = 8”,我们在两边都加上6,就有“8 + 6 = 8 + 6”;两边都减去11,就有“8 – 11 = 8 – 11”。问题1:你能用文字来叙述等式的这个性质吗?等式性质1、等式的两边加上(或减去)同一个数(或式子),结果仍相等。字母a、b、c可以是表示具体的数,也可以表示一个式子。如果a = b,那么a ±c = 2.1.2 等式的性质探求新知请同学们再仔细观察课本第71页图2.1--3问题2:你能用文字来叙述等式的这个性质吗?等式性质2、等式的两边乘同一个数,或除以同一个不为0的数。, 结果仍相等。如果a = b,那么ac = ;
如果a = b(C≠0),那么 =bc问题3:你能再举几个运用等式性质的例子吗?2.1.2 等式的性质应用举例方程是含有未知数的等式,我们可以运用等式的性质来解方程例1、利用等式的性质解下列方程:
(1)x + 7 = 26 ; (2)- 5 x = 20.解:(1)两边减 7 ,得x + 7 – 7 = 26 – 7 于是 x = 19(2)两边同除以 – 5,得 于是 x = - 4 .问题1:怎样才能把方程x + 7 = 26转化为x = a 的形式?变形的依据是什么?问题2:式子“ – 5x”表示什么?我们把其中的 – 5 叫做这个式子的系数,你能运用等式的性质把方程 – 5 x = 20转化为x = a 的形式吗?小结:请你归纳一下解一元一次方程的依据和结果形式。例2(补充)小涵的妈妈从商店买回一条裤子,小涵问妈妈:“这条裤子需要多少钱?”妈妈说:“按标价的八折是36元。”你知道标价是多少元吗?巩固练习:
(1)分别说出下列各式子的系数:
3x, - 7m , , a, - x,
(2)利用等式的性质解下列方程:
(1)x – 5 = 6; (2)0.3x = 45; (3) - y = 0.6;
(4)小结提高(1)等式的性质有哪几条?用字母怎样表示?字母代表什么?
(2)解方程的依据是什么?最终必须化为什么形式?
(3)在字母与数字的乘积中,数字因数又叫做这个式子的系数。作业:
(1)x = 3 是下列哪个方程的解? ( )
A、3x + 9 = 0 B、x = 10 – 4x
C、x(x – 2)= 3 D、2x – 7 = 12
(2)方程 的解是 ( )
A、- 3 B、 C、12 D、- 12
(3)已知x – 5 与2x – 4 的值互为相反数,列出关于x 的方程。
(4)某班开展为贫困山区学校捐书活动,捐的书比平均每人捐 3 本多 21 本,比平均每人捐4本少 27 本,求这个班有多少名学生?如果设这个班有x 名学生,请列出关于x 的方程。问题:你能用估算的方法求下列方程的解吗?
(1)3x – 5 = 22; (2)0.28 – 0.13y = 0.27y + 1.第(1)题用估算比较简单解答,第(2)题较复杂,估算比较困难。我们必须学习解一元一次方程的其他方法。2.1.2 等式的性质探求新知请同学们仔细观察课本第71页图2.1--2归纳:等式就像平衡的天平,它具有与上面的事实同样的性质。比如“8 = 8”,我们在两边都加上6,就有“8 + 6 = 8 + 6”;两边都减去11,就有“8 – 11 = 8 – 11”。问题1:你能用文字来叙述等式的这个性质吗?等式性质1、等式的两边加上(或减去)同一个数(或式子),结果仍相等。字母a、b、c可以是表示具体的数,也可以表示一个式子。如果a = b,那么a ±c = 2.1.2 等式的性质探求新知请同学们再仔细观察课本第71页图2.1--3问题2:你能用文字来叙述等式的这个性质吗?等式性质2、等式的两边乘同一个数,或除以同一个不为0的数。, 结果仍相等。如果a = b,那么ac = ;
如果a = b(C≠0),那么 =bc问题3:你能再举几个运用等式性质的例子吗?2.1.2 等式的性质应用举例方程是含有未知数的等式,我们可以运用等式的性质来解方程例1、利用等式的性质解下列方程:
(1)x + 7 = 26 ; (2)- 5 x = 20.解:(1)两边减 7 ,得x + 7 – 7 = 26 – 7 于是 x = 19(2)两边同除以 – 5,得 于是 x = - 4 .问题1:怎样才能把方程x + 7 = 26转化为x = a 的形式?变形的依据是什么?问题2:式子“ – 5x”表示什么?我们把其中的 – 5 叫做这个式子的系数,你能运用等式的性质把方程 – 5 x = 20转化为x = a 的形式吗?小结:请你归纳一下解一元一次方程的依据和结果形式。例2(补充)小涵的妈妈从商店买回一条裤子,小涵问妈妈:“这条裤子需要多少钱?”妈妈说:“按标价的八折是36元。”你知道标价是多少元吗?巩固练习:
(1)分别说出下列各式子的系数:
3x, - 7m , , a, - x,
(2)利用等式的性质解下列方程:
(1)x – 5 = 6; (2)0.3x = 45; (3) - y = 0.6;
(4)小结提高(1)等式的性质有哪几条?用字母怎样表示?字母代表什么?
(2)解方程的依据是什么?最终必须化为什么形式?
(3)在字母与数字的乘积中,数字因数又叫做这个式子的系数。作业:
