八年级数学上册试题 第7章 平行线的证明 单元测试 北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 第7章 平行线的证明 单元测试 北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 11:54:00 | ||
图片预览



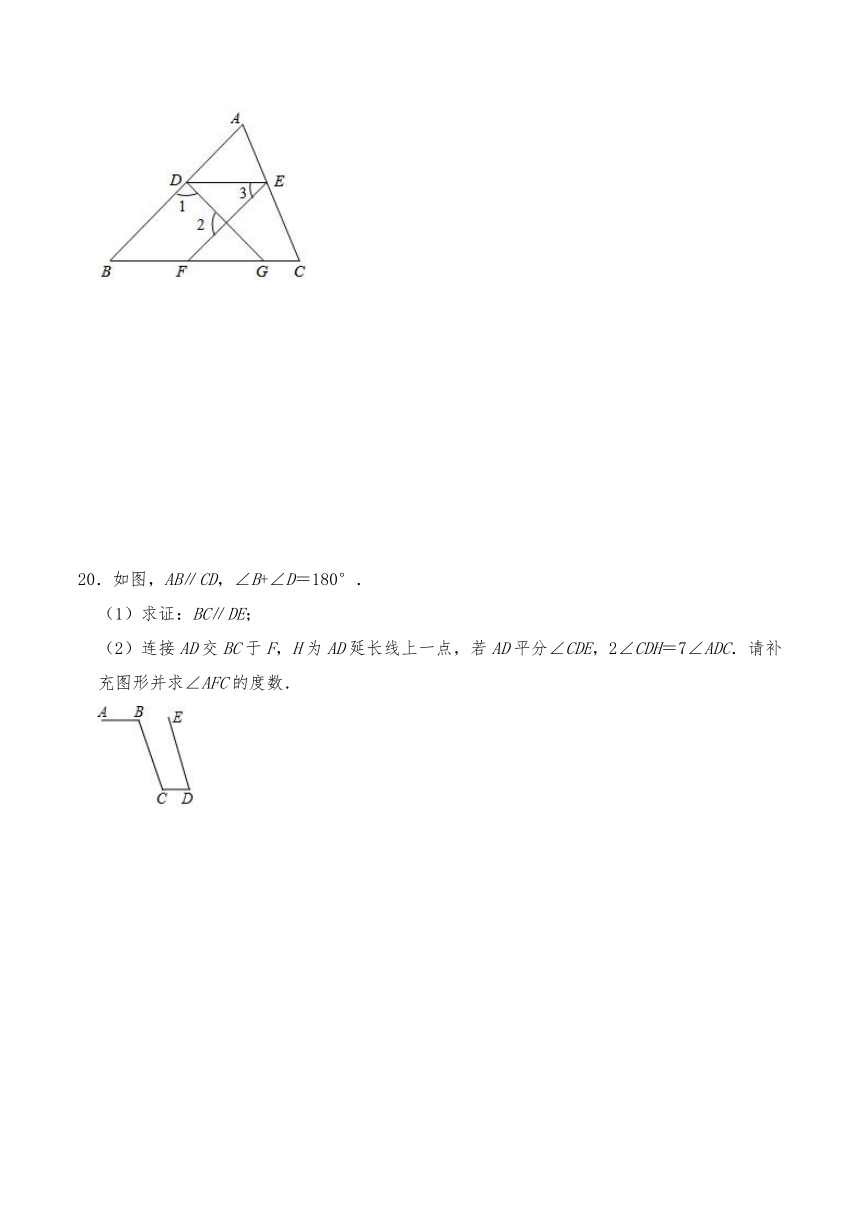
文档简介
第7章平行线的证明单元测试
一、选择题(本大题共10小题,每小题3分,共30分)
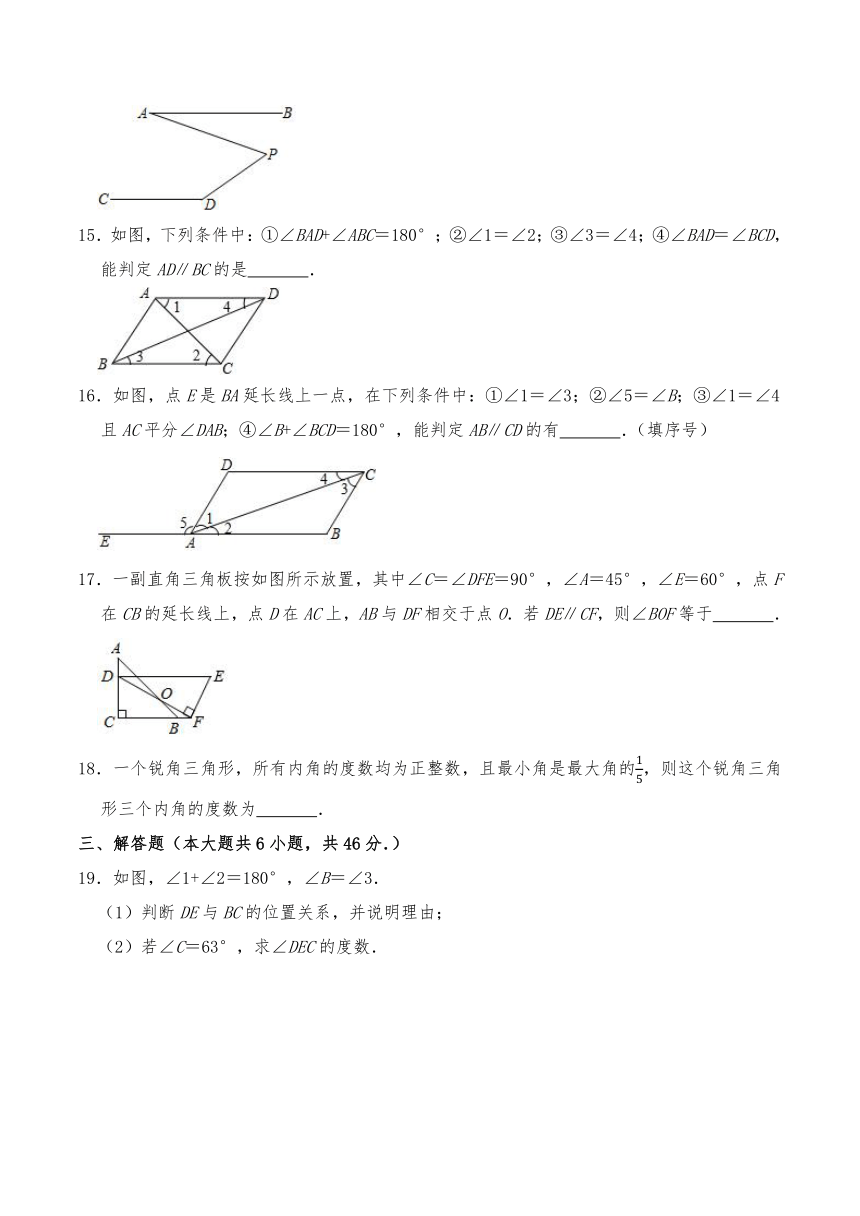
1.如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=43°,那么∠2的度数是( )
A.48° B.107° C.92° D.73°
2.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=120°,∠AOF的度数是( )
A.20° B.30° C.40° D.60°
3.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE∠EDC B.∠ABE+∠EDC=180°
C.∠EDC∠ABE=90° D.∠ABE∠EDC=90°
4.下列说法正确的有( )
①平面内,不相交的两条直线是平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平面内,过一点有且只有一条直线与已知直线平行;
④相等的角是对顶角;
⑤两角之和为180°,这两个角一定邻补角;
⑥P是直线a外一点,A、B、C分别是a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1.
A.1个 B.2个 C.3个 D.4个
5.下列命题是真命题的是( )
A.若a>b,则ac2>bc2
B.立方根等于本身的数是0和1
C.调查公民保护环境的意识,适合普查
D.一个角的补角比它的余角大90°
6.下列命题是真命题的是( )
A.如果两角是同位角,那么这两角一定相等
B.如果a2=b2,那么a=b
C.立方根是本身的数是0和1
D.等角或同角的余角相等
7.如图,点E在AB的延长线上,下列条件中可以判断AB∥CD的是( )
A.∠A=∠CBE B.∠A+∠CBA=180°
C.∠A=∠C D.∠C=∠CBE
8.如图下列条件中,不能判定直线AB∥CD的是(∠1=∠ACD)( )
A.∠1+∠A=180° B.∠2=∠B C.∠3=∠A D.∠3=∠B
9.如图,CD、BD分别平分∠ACE、∠ABC,∠A=70°,则∠BDC=( )
A.35° B.25° C.70° D.60°
10.如图,已知点E,D分别在△ABC边BA和CA的延长线上,CF和EF分别平分∠ACB和∠AED.如果∠B=70°,∠D=50°,则∠F的度数是( )
A.50° B.55° C.60° D.65°
二、填空题(本大题共8小题,每小题3分,共24分)
11.命题:①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短.其中真命题是 (填序号).
12.有下列命题:
①无理数是无限不循环小数;
②平方根与立方根相等的数有1和0;
③若a⊥b,b⊥c,则a⊥c;
④邻补角是互补的角;
⑤无理数包括正无理数、零、负无理数.
其中正确的有 个.
13.如图,已知直线a⊥c,b⊥c,若∠1=110°,则∠2的度数是 .
14.如图,AB∥CD,∠A=20°,∠CDP=145°,则∠P= °.
15.如图,下列条件中:①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠BCD,能判定AD∥BC的是 .
16.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
17.一副直角三角板按如图所示放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上,点D在AC上,AB与DF相交于点O.若DE∥CF,则∠BOF等于 .
18.一个锐角三角形,所有内角的度数均为正整数,且最小角是最大角的,则这个锐角三角形三个内角的度数为 .
三、解答题(本大题共6小题,共46分.)
19.如图,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并说明理由;
(2)若∠C=63°,求∠DEC的度数.
20.如图,AB∥CD,∠B+∠D=180°.
(1)求证:BC∥DE;
(2)连接AD交BC于F,H为AD延长线上一点,若AD平分∠CDE,2∠CDH=7∠ADC.请补充图形并求∠AFC的度数.
21.如图,△ABC中,点E和F分别在AB和AC上,点D和H都在BC上,EH和DF交于点G,∠1+∠2=180°,∠3=∠B.请说明EF和BC的位置关系,并说明理由.
22.如图,在△ABC中,∠B=40°,∠C=60°,点D,E分别在边BC,AC上,且DE∥AB.若∠CAD=40°.求∠ADE的度数.
23.如图,△ABC中,∠B=2∠C,AE平分∠BAC.
(1)若AD⊥BC于D,∠C=35°,求∠DAE的大小;
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC.
24.△ABC中,∠C=70°,点D、E分别是△ABC边AC、BC上的两个定点,点P是平面内一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
初探:
(1)如图1,若点P在线段AB上运动,
①当∠α=60°时,则∠1+∠2= °;
②∠α、∠1、∠2之间的关系为: .
再探:
(2)若点P运动到边AB的延长线上,如图2,则∠α、∠1、∠2之间有何关系?并说明理由.
拓展:
(3)请你试着给出一个点P的其他位置,在图3中补全图形,并写出此时∠α、∠1、∠2之间的关系: .
答案
一、选择题
B.B.C.B.D.D.D.D.A.C.
二、填空题
11.①②④.
12.1.
13.100°.
14.55.
15.①②③.
16.③④.
17.15°.
18.17°,78°,85°.
三、解答题
19.(1)DE∥BC.
理由:∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC;
(2)∵DE∥BC,
∴∠C+∠DEC=180°,
∵∠C=63°,
∴∠DEC=117°.
20.(1)∵AB∥CD,
∴∠B=∠C,
又∵∠B+∠D=180°,
∴∠C+∠D=180°,
∴BC∥DE;
(2)如图,
∵2∠CDH=7∠ADC,
∴∠CDH∠ADC,
∵BC∥DE,
∴∠ADC+∠CDH=180°,
∴180°,
∴,
∴∠ADC=40°,
∵AD平分∠CDE,
∴∠CDE=2∠ADC=2×40°=80°,
∵BC∥DE,
∴∠BCD+∠CDE=180°,
∴∠BCD=100°,
∴∠AFC=∠BCD+∠CDA=100°+40°=140°.
21.EF∥BC.
理由:∵∠1+∠2=180°,∠2=∠DGE,
∴∠DGE+∠1=180°,
∴AB∥DF,
∴∠FDC=∠B,
又∵∠3=∠B,
∴∠3=∠FDC,
∴EF∥BC.
22.在△ABC中,∠BAC+∠B+∠C=180°.
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵∠BAD=∠BAC﹣∠CAD,∠CAD=40°,
∴∠BAD=80°﹣40°=40°,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠ADE=40°.
23.(1)解:∵∠C=35°,∠B=2∠C,
∴∠B=70°,
∴∠BAC=75°,
∵AE平分∠BAC,
∴∠EAC=37.5°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=55°,
∴∠DAE=55°﹣37.5°=17.5°;
(2)证明:∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC∠BAC(180°﹣∠B﹣∠C)(180°﹣3∠C)=90°∠C,
∵∠DAE=∠DAC﹣∠EAC,
∴∠DAE=∠DAC﹣(90°∠C)=90°﹣∠C﹣90°∠C∠C,
∴∠FECC,
∴∠C=2∠FEC.
24.(1)①如图1中,连接PC.
∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DCP+∠ECP+∠EPC=∠ACB+∠DPE=∠ACB+∠α,
∵∠ACB=70°,∠α=60°,
∴∠1+∠2=60°+70°=130°.
②由①可知,∠1+∠2=∠ACB+∠α=70°+∠α,
故答案为130,70°+∠α.
(2)结论:∠1=70°+∠2+∠α.
理由:如图2中,
∵∠1=∠C+∠CFD,∠CFD=∠2+∠α,
∴∠1=70°+∠2+∠α.
(3)结论:∠1+∠2=430°﹣∠α.
理由:如图3中,
∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DCP+∠ECP+∠EPC=∠ACB+360°﹣∠DPE=70°+360°﹣∠α,
∴∠1+∠2=430°﹣∠α.
故答案为∠1+∠2=430°﹣∠α.
一、选择题(本大题共10小题,每小题3分,共30分)
1.如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=43°,那么∠2的度数是( )
A.48° B.107° C.92° D.73°
2.如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=120°,∠AOF的度数是( )
A.20° B.30° C.40° D.60°
3.如图,AB∥CD,BF平分∠ABE,且BF⊥DE垂足为F,则∠ABE与∠EDC的数量关系是( )
A.∠ABE∠EDC B.∠ABE+∠EDC=180°
C.∠EDC∠ABE=90° D.∠ABE∠EDC=90°
4.下列说法正确的有( )
①平面内,不相交的两条直线是平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平面内,过一点有且只有一条直线与已知直线平行;
④相等的角是对顶角;
⑤两角之和为180°,这两个角一定邻补角;
⑥P是直线a外一点,A、B、C分别是a上的三点,PA=1,PB=2,PC=3,则点P到直线a的距离一定是1.
A.1个 B.2个 C.3个 D.4个
5.下列命题是真命题的是( )
A.若a>b,则ac2>bc2
B.立方根等于本身的数是0和1
C.调查公民保护环境的意识,适合普查
D.一个角的补角比它的余角大90°
6.下列命题是真命题的是( )
A.如果两角是同位角,那么这两角一定相等
B.如果a2=b2,那么a=b
C.立方根是本身的数是0和1
D.等角或同角的余角相等
7.如图,点E在AB的延长线上,下列条件中可以判断AB∥CD的是( )
A.∠A=∠CBE B.∠A+∠CBA=180°
C.∠A=∠C D.∠C=∠CBE
8.如图下列条件中,不能判定直线AB∥CD的是(∠1=∠ACD)( )
A.∠1+∠A=180° B.∠2=∠B C.∠3=∠A D.∠3=∠B
9.如图,CD、BD分别平分∠ACE、∠ABC,∠A=70°,则∠BDC=( )
A.35° B.25° C.70° D.60°
10.如图,已知点E,D分别在△ABC边BA和CA的延长线上,CF和EF分别平分∠ACB和∠AED.如果∠B=70°,∠D=50°,则∠F的度数是( )
A.50° B.55° C.60° D.65°
二、填空题(本大题共8小题,每小题3分,共24分)
11.命题:①邻补角互补;②对顶角相等;③同旁内角互补;④两点之间线段最短.其中真命题是 (填序号).
12.有下列命题:
①无理数是无限不循环小数;
②平方根与立方根相等的数有1和0;
③若a⊥b,b⊥c,则a⊥c;
④邻补角是互补的角;
⑤无理数包括正无理数、零、负无理数.
其中正确的有 个.
13.如图,已知直线a⊥c,b⊥c,若∠1=110°,则∠2的度数是 .
14.如图,AB∥CD,∠A=20°,∠CDP=145°,则∠P= °.
15.如图,下列条件中:①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠BCD,能判定AD∥BC的是 .
16.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
17.一副直角三角板按如图所示放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上,点D在AC上,AB与DF相交于点O.若DE∥CF,则∠BOF等于 .
18.一个锐角三角形,所有内角的度数均为正整数,且最小角是最大角的,则这个锐角三角形三个内角的度数为 .
三、解答题(本大题共6小题,共46分.)
19.如图,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并说明理由;
(2)若∠C=63°,求∠DEC的度数.
20.如图,AB∥CD,∠B+∠D=180°.
(1)求证:BC∥DE;
(2)连接AD交BC于F,H为AD延长线上一点,若AD平分∠CDE,2∠CDH=7∠ADC.请补充图形并求∠AFC的度数.
21.如图,△ABC中,点E和F分别在AB和AC上,点D和H都在BC上,EH和DF交于点G,∠1+∠2=180°,∠3=∠B.请说明EF和BC的位置关系,并说明理由.
22.如图,在△ABC中,∠B=40°,∠C=60°,点D,E分别在边BC,AC上,且DE∥AB.若∠CAD=40°.求∠ADE的度数.
23.如图,△ABC中,∠B=2∠C,AE平分∠BAC.
(1)若AD⊥BC于D,∠C=35°,求∠DAE的大小;
(2)若EF⊥AE交AC于F,求证:∠C=2∠FEC.
24.△ABC中,∠C=70°,点D、E分别是△ABC边AC、BC上的两个定点,点P是平面内一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
初探:
(1)如图1,若点P在线段AB上运动,
①当∠α=60°时,则∠1+∠2= °;
②∠α、∠1、∠2之间的关系为: .
再探:
(2)若点P运动到边AB的延长线上,如图2,则∠α、∠1、∠2之间有何关系?并说明理由.
拓展:
(3)请你试着给出一个点P的其他位置,在图3中补全图形,并写出此时∠α、∠1、∠2之间的关系: .
答案
一、选择题
B.B.C.B.D.D.D.D.A.C.
二、填空题
11.①②④.
12.1.
13.100°.
14.55.
15.①②③.
16.③④.
17.15°.
18.17°,78°,85°.
三、解答题
19.(1)DE∥BC.
理由:∵∠1+∠2=180°,
∴AB∥EF,
∴∠ADE=∠3,
∵∠B=∠3,
∴∠ADE=∠B,
∴DE∥BC;
(2)∵DE∥BC,
∴∠C+∠DEC=180°,
∵∠C=63°,
∴∠DEC=117°.
20.(1)∵AB∥CD,
∴∠B=∠C,
又∵∠B+∠D=180°,
∴∠C+∠D=180°,
∴BC∥DE;
(2)如图,
∵2∠CDH=7∠ADC,
∴∠CDH∠ADC,
∵BC∥DE,
∴∠ADC+∠CDH=180°,
∴180°,
∴,
∴∠ADC=40°,
∵AD平分∠CDE,
∴∠CDE=2∠ADC=2×40°=80°,
∵BC∥DE,
∴∠BCD+∠CDE=180°,
∴∠BCD=100°,
∴∠AFC=∠BCD+∠CDA=100°+40°=140°.
21.EF∥BC.
理由:∵∠1+∠2=180°,∠2=∠DGE,
∴∠DGE+∠1=180°,
∴AB∥DF,
∴∠FDC=∠B,
又∵∠3=∠B,
∴∠3=∠FDC,
∴EF∥BC.
22.在△ABC中,∠BAC+∠B+∠C=180°.
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵∠BAD=∠BAC﹣∠CAD,∠CAD=40°,
∴∠BAD=80°﹣40°=40°,
∵DE∥AB,
∴∠ADE=∠BAD,
∴∠ADE=40°.
23.(1)解:∵∠C=35°,∠B=2∠C,
∴∠B=70°,
∴∠BAC=75°,
∵AE平分∠BAC,
∴∠EAC=37.5°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=55°,
∴∠DAE=55°﹣37.5°=17.5°;
(2)证明:∵EF⊥AE,
∴∠AEF=90°,
∴∠AED+∠FEC=90°,
∵∠DAE+∠AED=90°,
∴∠DAE=∠FEC,
∵AE平分∠BAC,
∴∠EAC∠BAC(180°﹣∠B﹣∠C)(180°﹣3∠C)=90°∠C,
∵∠DAE=∠DAC﹣∠EAC,
∴∠DAE=∠DAC﹣(90°∠C)=90°﹣∠C﹣90°∠C∠C,
∴∠FECC,
∴∠C=2∠FEC.
24.(1)①如图1中,连接PC.
∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DCP+∠ECP+∠EPC=∠ACB+∠DPE=∠ACB+∠α,
∵∠ACB=70°,∠α=60°,
∴∠1+∠2=60°+70°=130°.
②由①可知,∠1+∠2=∠ACB+∠α=70°+∠α,
故答案为130,70°+∠α.
(2)结论:∠1=70°+∠2+∠α.
理由:如图2中,
∵∠1=∠C+∠CFD,∠CFD=∠2+∠α,
∴∠1=70°+∠2+∠α.
(3)结论:∠1+∠2=430°﹣∠α.
理由:如图3中,
∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DCP+∠ECP+∠EPC=∠ACB+360°﹣∠DPE=70°+360°﹣∠α,
∴∠1+∠2=430°﹣∠α.
故答案为∠1+∠2=430°﹣∠α.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
