八年级数学上册试题 第7章 平行线的证明 单元测试卷 北师大版(含答案)
文档属性
| 名称 | 八年级数学上册试题 第7章 平行线的证明 单元测试卷 北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 109.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 11:54:50 | ||
图片预览



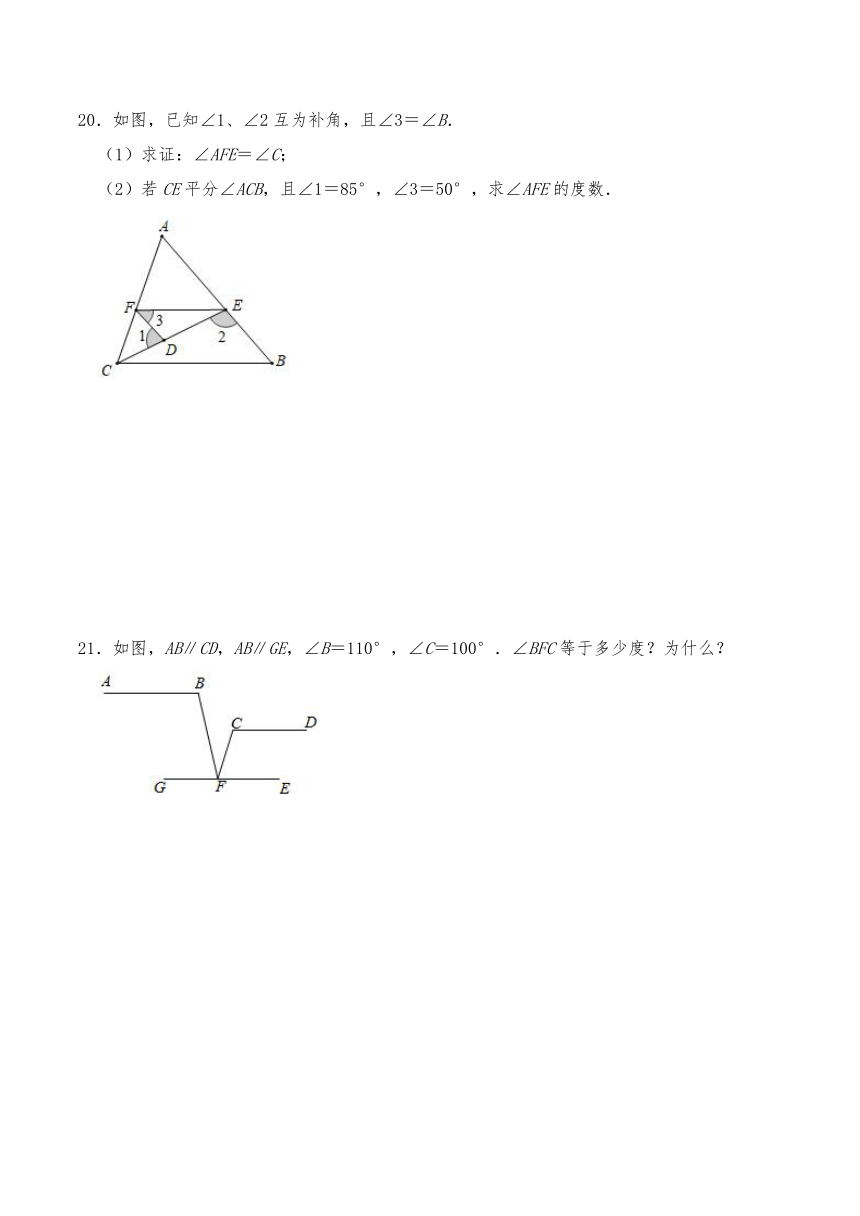
文档简介
第7章平行线的证明单元测试卷
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列命题中,正确的是( )
A.相等的两个角是对顶角
B.一条直线有只有一条垂线
C.一个角一定不等于它的余角
D.从直线外一点到这条直线上的各点所连结的线段中,垂线段最短
2.下列命题:①如果a>b,那么|a|>|b|:②如果ac2>bc2,那么a>b;③同旁内角互补;④若∠α与∠β互余,∠β与∠γ互余,则∠α与∠γ互余.真命题的个数为( )
A.0 B.1 C.2 D.3
3.下列语句中,不是命题的是( )
A.如果a+b=0,那么a、b互为相反数
B.内错角相等
C.已知a2=4,a的值是多少?
D.负数大于正数
4.如图,l1∥l2,则∠1、∠2、∠3关系是( )
A.∠2>∠1+∠3 B.无法确定 C.∠3=∠1﹣∠2 D.∠2=∠1+∠3
5.如图,已知AB∥CD,∠A=60°,∠ECD=120°,∠ECA的度数是( )
A.90° B.120° C.135° D.150°
6.如图,下列判断正确的是( )
A.若∠1=∠2,则AD∥BC
B.若∠3=∠4,则AD∥BC
C.若∠A+∠ABC=180°,则AB∥CD
D.若∠A+∠ADC=180°,则AD∥BC
7.如图,O是直线AB上一点,OE平分∠BOD,OF⊥OE,∠D=110°,添加一个条件,仍不能判定AB∥CD,添加的条件可能是( )
A.∠BOE=55° B.∠DOF=35°
C.∠BOE+∠AOF=90° D.∠AOF=35°
8.如图,在三角形ABC中,∠ABC=50°,∠ACB=24°,BD平分∠ABC,CD平分∠ACB,其角平分线相交于D,则∠BDC=( )
A.141° B.142° C.143° D.145°
9.如图,在△ABC中,∠ACB=90°,点D在AB上,将△BDC沿CD折叠,点B落在AC边上的点B′处,若∠ADB′=20°,则∠A的度数为( )
A.20° B.25° C.35° D.40°
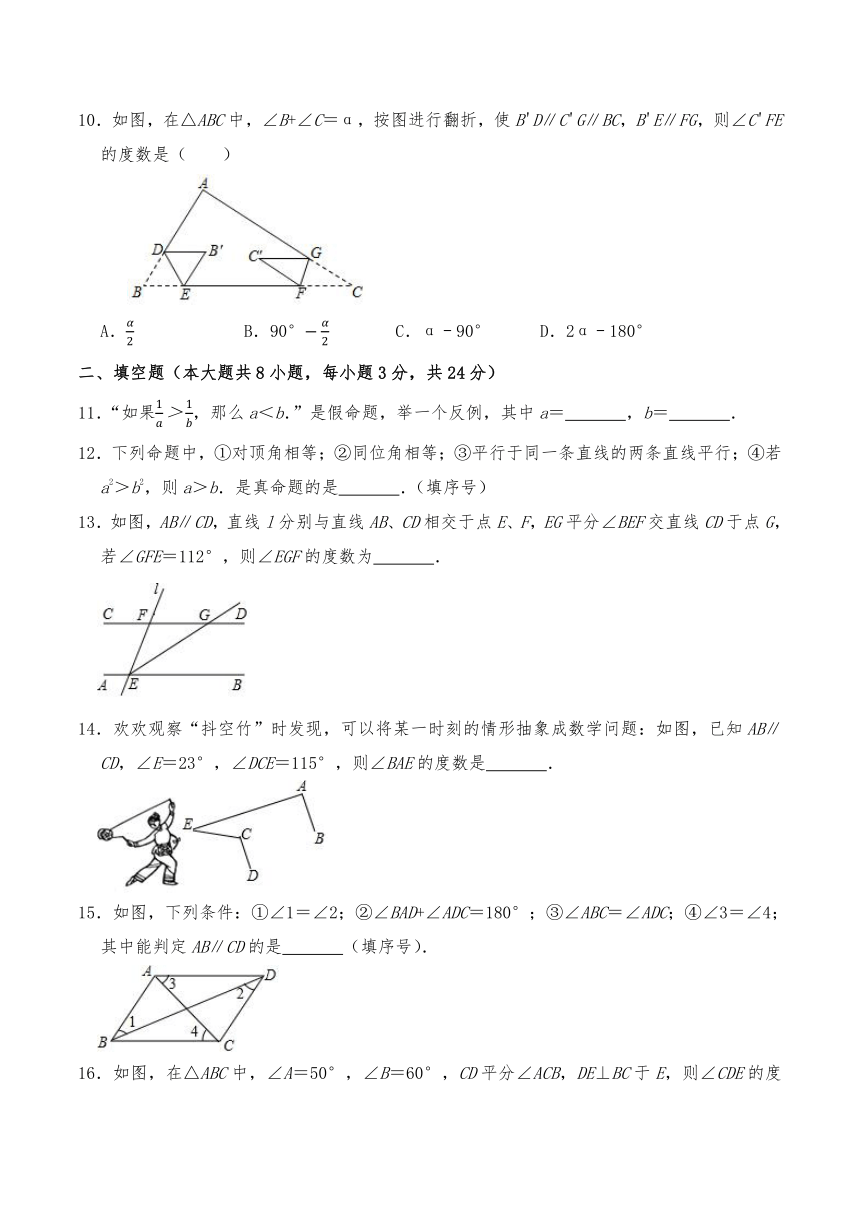
10.如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G∥BC,B'E∥FG,则∠C'FE的度数是( )
A. B.90° C.α﹣90° D.2α﹣180°
二、填空题(本大题共8小题,每小题3分,共24分)
11.“如果,那么a<b.”是假命题,举一个反例,其中a= ,b= .
12.下列命题中,①对顶角相等;②同位角相等;③平行于同一条直线的两条直线平行;④若a2>b2,则a>b.是真命题的是 .(填序号)
13.如图,AB∥CD,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠GFE=112°,则∠EGF的度数为 .
14.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠E=23°,∠DCE=115°,则∠BAE的度数是 .
15.如图,下列条件:①∠1=∠2;②∠BAD+∠ADC=180°;③∠ABC=∠ADC;④∠3=∠4;其中能判定AB∥CD的是 (填序号).
16.如图,在△ABC中,∠A=50°,∠B=60°,CD平分∠ACB,DE⊥BC于E,则∠CDE的度数为 .
17.如图所示,在△ABC中,∠A=50°,点D在△ABC的内部,并且∠DBA∠ABC,∠DCA∠ACB,则∠D的度数是 .
18.如图,在△ABC中,AD是BC边上的高,且∠ACB=∠BAD,AE平分∠CAD,交BC于点E,过点E作EF∥AC,分别交AB、AD于点F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF;③∠BAE=∠BEA;④∠B=2∠AEF,其中正确的有 .
三、解答题(本大题共6小题,共46分.)
19.如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠E=∠F,CE∥DF,求证:∠A=∠1.
20.如图,已知∠1、∠2互为补角,且∠3=∠B.
(1)求证:∠AFE=∠C;
(2)若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE的度数.
21.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
22.如图,在△ABC中,BD是∠ABC的角平分线,作DE∥BC交AB于点E,∠A=62°,∠BDC=100°,求∠BED的度数.
23.现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是 .
研究(2):如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是 ;
研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.
24.直线MN与PQ相互垂直,垂足为点O,点A在射线OQ上运动,点B在射线OM上运动,点A、点B均不与点O重合.
(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,求∠AIB的度数;
(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.
①若∠BAO=40°,则∠ADB= 度(直接写出结果,不需说理);
②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.
(3)如图3,已知点E在BA的延长线上,∠BAO的角平分线AI、∠OAE的角平分线AF与∠BOP的角平分线所在的直线分别相交于点D、F,在△ADF中,如果有一个角的度数是另一个角的4倍,请直接写出∠ABO的度数.
答案
一、选择题
D.B.C.D.B.B.C.C.C.D.
二、填空题
11.1,﹣2.
12.①③.
13.34°.
14.92°.
15.①②.
16.55°.
17.76°.
18.①③④.
三、解答题(本大题共6小题,共46分.)
19.证明:∵CE∥DF,
∴∠F=∠2,
∵∠E=∠F,
∴∠E=∠2,
∴AE∥BF,
∴∠A=∠1.
20.证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=85°,∠3=50°,
∴∠FED=85°﹣50°=35°,
∵EF∥BC,
∴∠BCE=∠FED=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∴∠AFE=∠ACB=70°.
21.∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
22.∵∠A+∠ABD=∠BDC,∠A=62°,∠BDC=100°,
∴∠ABD=38°,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
又∵DE∥BC,
∴∠CBD=∠BDE,
∴∠BDE=∠ABD=38°,
∴∠BED=180°﹣∠ABD﹣∠BDE=104°.
23.(1)如图1,∠1=2∠A,理由是:
由折叠得:∠A=∠DA′A,
∵∠1=∠A+∠DA′A,
∴∠1=2∠A;
故答案为:∠1=2∠A;
(2)如图2,猜想:∠1+∠2=2∠A,理由是:
由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,
∵∠ADB+∠AEC=360°,
∴∠1+∠2=360°﹣∠ADE﹣∠A′DE﹣∠AED﹣∠A′ED=360°﹣2∠ADE﹣2∠AED,
∴∠1+∠2=2(180°﹣∠ADE﹣∠AED)=2∠A;
故答案为:∠1+∠2=2∠A;
(3)如图3,∠2﹣∠1=2∠DAE,理由是:
∵∠2=∠AFE+∠DAE,∠AFE=∠A′+∠1,
∴∠2=∠A′+∠DAE+∠1,
∵∠DAE=∠A′,
∴∠2=2∠DAE+∠1,
∴∠2﹣∠1=2∠DAE.
故答案为:(1)∠1=2∠A;
(2)∠1+∠2=2∠A.
24.(1)如图1中,
∵MN⊥PQ,
∴∠AOB=90°,∵∠OAB=40°,
∴∠ABO=90°﹣∠OAB=50°,
∵AI平分∠BAO,BI平分∠ABO,
∴∠IBAABO=25°,∠IAB∠OAB=20°,
∴∠AIB=180°﹣(∠IBA+∠IAB)=135°.
(2)如图2中,
①∵∠MBA=∠AOB+∠BAO=90°+40°=130°,
∵AI平分∠BAO,BC平分∠ABM,
∴∠CBA∠MBA=65°,∠BAI∠BAO=20°,
∵∠CBA=∠D+∠BAD,
∴∠D=45°,
故答案为:45.
②不变,
理由:∵∠D=∠CBA﹣∠BAD∠MBA∠BAO(∠MBA﹣∠BAO)∠AOB90°=45°,
∴点A、B在运动的过程中,∠ADB=45°.
(3)如图3中,
∵∠BAO的角平分线AI、∠OAE的角平分线AF与∠BOP的角平分线所在的直线分别相交于点D、F,
∴∠DAO∠BAO,∠FAO∠EAP,
∴∠DAF∠BAOEAP180°=90°,
∴∠D=∠POD﹣∠DAO∠POB∠BAO(∠POB﹣∠BAO)∠ABO,
①当∠DAF=4∠D时,∠D=22.5°,
∴∠ABO=2∠D=45°.
②当∠DAF=4∠F时,∠F=22.5°,∠D=67.5°,
∴∠ABO=2∠D=135°(不合题意舍弃).
③当∠F=4∠D时,∠D=18°,
∴∠ABO=2∠D=36°.
④当∠D=4∠F时,∠D=72°,
∴∠ABO=2∠D=144°(不合题意舍弃).
综上所述,当∠ABO=45°或36°时,在△ADF中,有一个角的度数是另一个角的4倍.
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列命题中,正确的是( )
A.相等的两个角是对顶角
B.一条直线有只有一条垂线
C.一个角一定不等于它的余角
D.从直线外一点到这条直线上的各点所连结的线段中,垂线段最短
2.下列命题:①如果a>b,那么|a|>|b|:②如果ac2>bc2,那么a>b;③同旁内角互补;④若∠α与∠β互余,∠β与∠γ互余,则∠α与∠γ互余.真命题的个数为( )
A.0 B.1 C.2 D.3
3.下列语句中,不是命题的是( )
A.如果a+b=0,那么a、b互为相反数
B.内错角相等
C.已知a2=4,a的值是多少?
D.负数大于正数
4.如图,l1∥l2,则∠1、∠2、∠3关系是( )
A.∠2>∠1+∠3 B.无法确定 C.∠3=∠1﹣∠2 D.∠2=∠1+∠3
5.如图,已知AB∥CD,∠A=60°,∠ECD=120°,∠ECA的度数是( )
A.90° B.120° C.135° D.150°
6.如图,下列判断正确的是( )
A.若∠1=∠2,则AD∥BC
B.若∠3=∠4,则AD∥BC
C.若∠A+∠ABC=180°,则AB∥CD
D.若∠A+∠ADC=180°,则AD∥BC
7.如图,O是直线AB上一点,OE平分∠BOD,OF⊥OE,∠D=110°,添加一个条件,仍不能判定AB∥CD,添加的条件可能是( )
A.∠BOE=55° B.∠DOF=35°
C.∠BOE+∠AOF=90° D.∠AOF=35°
8.如图,在三角形ABC中,∠ABC=50°,∠ACB=24°,BD平分∠ABC,CD平分∠ACB,其角平分线相交于D,则∠BDC=( )
A.141° B.142° C.143° D.145°
9.如图,在△ABC中,∠ACB=90°,点D在AB上,将△BDC沿CD折叠,点B落在AC边上的点B′处,若∠ADB′=20°,则∠A的度数为( )
A.20° B.25° C.35° D.40°
10.如图,在△ABC中,∠B+∠C=α,按图进行翻折,使B'D∥C'G∥BC,B'E∥FG,则∠C'FE的度数是( )
A. B.90° C.α﹣90° D.2α﹣180°
二、填空题(本大题共8小题,每小题3分,共24分)
11.“如果,那么a<b.”是假命题,举一个反例,其中a= ,b= .
12.下列命题中,①对顶角相等;②同位角相等;③平行于同一条直线的两条直线平行;④若a2>b2,则a>b.是真命题的是 .(填序号)
13.如图,AB∥CD,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠GFE=112°,则∠EGF的度数为 .
14.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠E=23°,∠DCE=115°,则∠BAE的度数是 .
15.如图,下列条件:①∠1=∠2;②∠BAD+∠ADC=180°;③∠ABC=∠ADC;④∠3=∠4;其中能判定AB∥CD的是 (填序号).
16.如图,在△ABC中,∠A=50°,∠B=60°,CD平分∠ACB,DE⊥BC于E,则∠CDE的度数为 .
17.如图所示,在△ABC中,∠A=50°,点D在△ABC的内部,并且∠DBA∠ABC,∠DCA∠ACB,则∠D的度数是 .
18.如图,在△ABC中,AD是BC边上的高,且∠ACB=∠BAD,AE平分∠CAD,交BC于点E,过点E作EF∥AC,分别交AB、AD于点F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF;③∠BAE=∠BEA;④∠B=2∠AEF,其中正确的有 .
三、解答题(本大题共6小题,共46分.)
19.如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠E=∠F,CE∥DF,求证:∠A=∠1.
20.如图,已知∠1、∠2互为补角,且∠3=∠B.
(1)求证:∠AFE=∠C;
(2)若CE平分∠ACB,且∠1=85°,∠3=50°,求∠AFE的度数.
21.如图,AB∥CD,AB∥GE,∠B=110°,∠C=100°.∠BFC等于多少度?为什么?
22.如图,在△ABC中,BD是∠ABC的角平分线,作DE∥BC交AB于点E,∠A=62°,∠BDC=100°,求∠BED的度数.
23.现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
研究(1):如果折成图①的形状,使点A落在CE上,则∠1与∠A的数量关系是 .
研究(2):如果折成图②的形状,猜想∠1+∠2与∠A的数量关系是 ;
研究(3):如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.
24.直线MN与PQ相互垂直,垂足为点O,点A在射线OQ上运动,点B在射线OM上运动,点A、点B均不与点O重合.
(1)如图1,AI平分∠BAO,BI平分∠ABO,若∠BAO=40°,求∠AIB的度数;
(2)如图2,AI平分∠BAO,BC平分∠ABM,BC的反向延长线交AI于点D.
①若∠BAO=40°,则∠ADB= 度(直接写出结果,不需说理);
②点A、B在运动的过程中,∠ADB是否发生变化,若不变,试求∠ADB的度数;若变化,请说明变化规律.
(3)如图3,已知点E在BA的延长线上,∠BAO的角平分线AI、∠OAE的角平分线AF与∠BOP的角平分线所在的直线分别相交于点D、F,在△ADF中,如果有一个角的度数是另一个角的4倍,请直接写出∠ABO的度数.
答案
一、选择题
D.B.C.D.B.B.C.C.C.D.
二、填空题
11.1,﹣2.
12.①③.
13.34°.
14.92°.
15.①②.
16.55°.
17.76°.
18.①③④.
三、解答题(本大题共6小题,共46分.)
19.证明:∵CE∥DF,
∴∠F=∠2,
∵∠E=∠F,
∴∠E=∠2,
∴AE∥BF,
∴∠A=∠1.
20.证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=85°,∠3=50°,
∴∠FED=85°﹣50°=35°,
∵EF∥BC,
∴∠BCE=∠FED=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∴∠AFE=∠ACB=70°.
21.∠BFC等于30度,理由如下:
∵AB∥GE,
∴∠B+∠BFG=180°,
∵∠B=110°,
∴∠BFG=180°﹣110°=70°,
∵AB∥CD,AB∥GE,
∴CD∥GE,
∴∠C+∠CFE=180°,
∵∠C=100°.
∴∠CFE=180°﹣100°=80°,
∴∠BFC=180°﹣∠BFG﹣∠CFE=180°﹣70°﹣80°=30°.
22.∵∠A+∠ABD=∠BDC,∠A=62°,∠BDC=100°,
∴∠ABD=38°,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
又∵DE∥BC,
∴∠CBD=∠BDE,
∴∠BDE=∠ABD=38°,
∴∠BED=180°﹣∠ABD﹣∠BDE=104°.
23.(1)如图1,∠1=2∠A,理由是:
由折叠得:∠A=∠DA′A,
∵∠1=∠A+∠DA′A,
∴∠1=2∠A;
故答案为:∠1=2∠A;
(2)如图2,猜想:∠1+∠2=2∠A,理由是:
由折叠得:∠ADE=∠A′DE,∠AED=∠A′ED,
∵∠ADB+∠AEC=360°,
∴∠1+∠2=360°﹣∠ADE﹣∠A′DE﹣∠AED﹣∠A′ED=360°﹣2∠ADE﹣2∠AED,
∴∠1+∠2=2(180°﹣∠ADE﹣∠AED)=2∠A;
故答案为:∠1+∠2=2∠A;
(3)如图3,∠2﹣∠1=2∠DAE,理由是:
∵∠2=∠AFE+∠DAE,∠AFE=∠A′+∠1,
∴∠2=∠A′+∠DAE+∠1,
∵∠DAE=∠A′,
∴∠2=2∠DAE+∠1,
∴∠2﹣∠1=2∠DAE.
故答案为:(1)∠1=2∠A;
(2)∠1+∠2=2∠A.
24.(1)如图1中,
∵MN⊥PQ,
∴∠AOB=90°,∵∠OAB=40°,
∴∠ABO=90°﹣∠OAB=50°,
∵AI平分∠BAO,BI平分∠ABO,
∴∠IBAABO=25°,∠IAB∠OAB=20°,
∴∠AIB=180°﹣(∠IBA+∠IAB)=135°.
(2)如图2中,
①∵∠MBA=∠AOB+∠BAO=90°+40°=130°,
∵AI平分∠BAO,BC平分∠ABM,
∴∠CBA∠MBA=65°,∠BAI∠BAO=20°,
∵∠CBA=∠D+∠BAD,
∴∠D=45°,
故答案为:45.
②不变,
理由:∵∠D=∠CBA﹣∠BAD∠MBA∠BAO(∠MBA﹣∠BAO)∠AOB90°=45°,
∴点A、B在运动的过程中,∠ADB=45°.
(3)如图3中,
∵∠BAO的角平分线AI、∠OAE的角平分线AF与∠BOP的角平分线所在的直线分别相交于点D、F,
∴∠DAO∠BAO,∠FAO∠EAP,
∴∠DAF∠BAOEAP180°=90°,
∴∠D=∠POD﹣∠DAO∠POB∠BAO(∠POB﹣∠BAO)∠ABO,
①当∠DAF=4∠D时,∠D=22.5°,
∴∠ABO=2∠D=45°.
②当∠DAF=4∠F时,∠F=22.5°,∠D=67.5°,
∴∠ABO=2∠D=135°(不合题意舍弃).
③当∠F=4∠D时,∠D=18°,
∴∠ABO=2∠D=36°.
④当∠D=4∠F时,∠D=72°,
∴∠ABO=2∠D=144°(不合题意舍弃).
综上所述,当∠ABO=45°或36°时,在△ADF中,有一个角的度数是另一个角的4倍.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
