七年级数学上册试题 第4章《基本平面图形》单元测试卷 北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 第4章《基本平面图形》单元测试卷 北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 00:00:00 | ||
图片预览




文档简介
第4章《基本平面图形》测试卷
一、选择题(本大题共12小题,每小题3分,共36分。)
1.当分针指向12,时针这时恰好与分针成30°的角,此时是( )
A.9点钟 B.10点钟 C.11点钟或1点钟 D.2点钟或10点钟
2.下列说法正确的是( )
A.角的大小和开口的大小无关 B.互余、互补是指两个角之间的数量关系
C.单独的一个角也可以叫余角或补角 D.若三个角的和是直角,则他们互余
3.根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )
A. B.
C. D.
4.下列各图中直线的表示法正确的是( ).
A. B.
C. D.
5.下列说法正确的是( ).
A.两点之间的距离是两点间的直线长度
B.两点之间,射线最短
C.经过三点,只有一条直线
D.同角的余角相等
6.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
7.如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
A.商船在海岛的北偏西50°方向 B.海岛在商船的北偏西40°方向
C.海岛在商船的东偏南50°方向 D.商船在海岛的东偏南40°方向
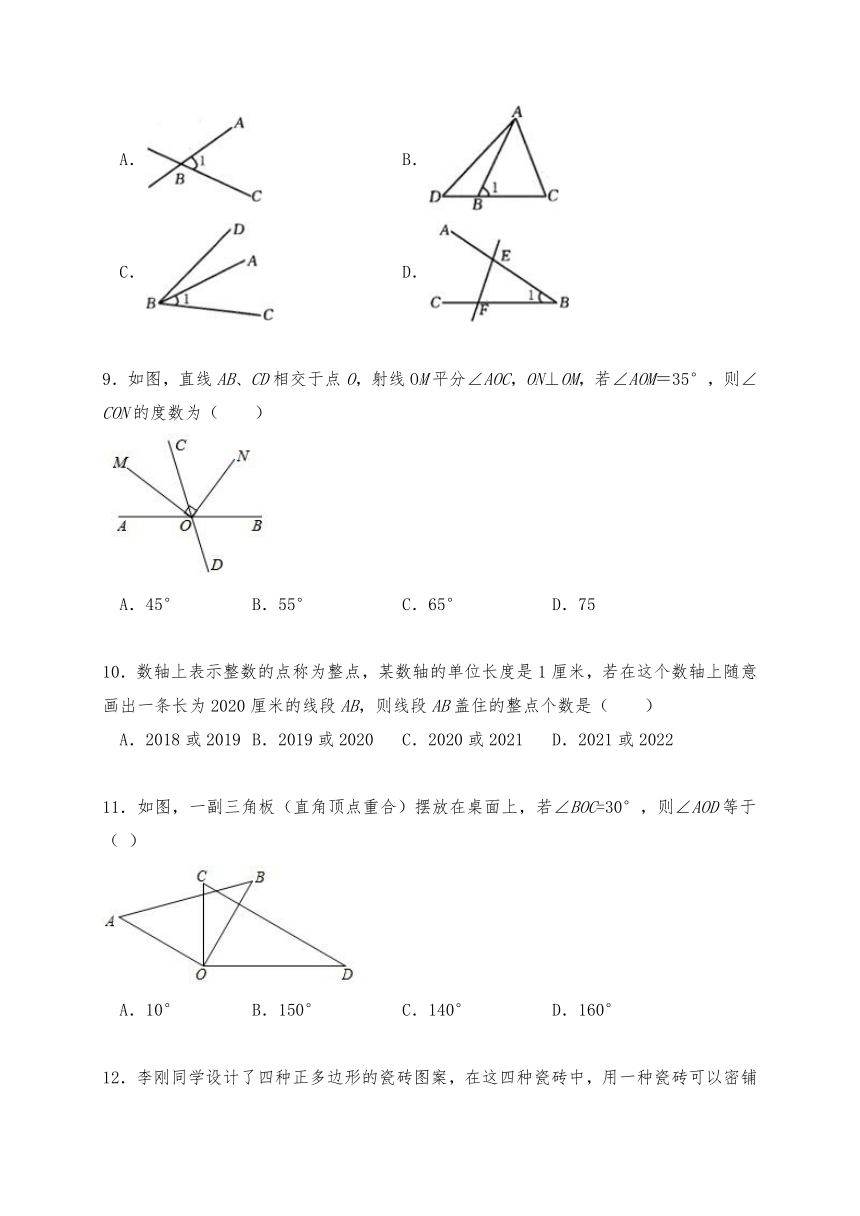
8.下图中,能用∠ABC,∠B,∠1三种方法表示同一个角的图形是( )
A. B.
C. D.
9.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.45° B.55° C.65° D.75
10.数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB,则线段AB盖住的整点个数是( )
A.2018或2019 B.2019或2020 C.2020或2021 D.2021或2022
11.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠BOC=30°,则∠AOD等于( )
A.10° B.150° C.140° D.160°
12.李刚同学设计了四种正多边形的瓷砖图案,在这四种瓷砖中,用一种瓷砖可以密铺平面的是( )
A.(1)(2)(4) B.(2)(3)(4)
C.(1)(3)(4) D.(1)(2)(3)
二、填空题(本大题共6小题,每小题3分,共18分)
13.如图,AB=6,BC=4,D、E分别是AB、BC的中点,则BD+BE=_____,根据公理:_______________,可知BD+BE_____DE.
14.在直线l上顺次取A、B、C三点,使得AB=3cm,BC=5cm,若点D是线段AC的中点,则线段DB的长度等于__cm.
15.如图所示,OD、OE是两条射线,A在射线OD上,B、C在射线OE上,则图有共有线段________条,分别是________;共有________条射线,分别是________.
16.已知线段AB=7cm,在直线AB上画线段BC,使它等于3cm,则线段AC=____cm.
17.书店、学校、食堂在同一个平面上,分别用点A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC应该是______________.
18.如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB=_______.
三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程)
19.已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若线段AC=6,BC=4,求线段MN的长度;
(2)若AB=a,求线段MN的长度;
(3)若将(1)小题中“点C在线段AB上”改为“点C在直线AB上”,(1)小题的结果会有变化吗 求出MN的长度.
20.小明发现这样一个问题:“在一次聚会中,共有6人参加,如果每两人都握一次手,共握几次手 ”通过思考,小明得出了答案, 那请问同学们:如果有n个人参加聚会,每两人都握一次手,一共要握多少次手呢
21.如图,M是线段AB的中点,点C在线段AB上,且AC=8cm,N是AC的中点,MN=6cm,求线段AB的长.
22.如图所示一只蚂蚁在A处,想到C处的最短路线,请画出简图,并说明理由.
23.已知线段AB上有三个定点C、D、E.
(1)图中共有几条线段?
(2)如果在线段CD上增加一点,则增加了几条线段?你能从中发现什么规律吗?
24.读下列语句,并分别画出图形:
(1)直线l经过A、B、C三点,点C在点A与点B之间;
(2)两条直线m与n相交于点P;
(3)线段a、b相交于点O,与线段c分别交于点P、Q.
答案
一、选择题
C.B.C.C.D.D.B.D.B.C.B.A.
二、填空题
13.5 两点之间线段最短 >
14.1
15.6 线段OA、OB、OC、BC、AC、AB 5 射线OD、OE、BE、AD、CE
16.10或4或4
17.165°
18.20°
三、解答题
19.
解:(1)∵ AC=6,BC=4,
∴ AB=6+4=10,
又∵ 点M是AC的中点,点N是BC的中点,
∴ MC=AM=AC,CN=BN=BC,
∴ MN=MC+CN=AC+BC=(AC+BC)=AB=5(cm).
(2)由(1)中已知AB=10cm求出MN=5cm,分析(1)的推算过程可知MN=AB,
故当AB=a时,MN=,
从而得到规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
(3)分类讨论:
当点C在点B的右侧时,如图可得:
;
当点C在线段AB上时,如(1);
当点C在点A的左侧时,不满足题意.
综上可得:点C在直线AB上时,MN的长为1或5.
20.
解:∵若有6个人参加聚会,则每个人都要与另外5个人握手一次,
∴一共要握手次,
又∵两个人之间握手的次数只能算作一次,
∴最后握手的总次数次;
∵若有n个人参加聚会,则每个人都要与另外n-1个人握手一次,
∴一共要握手次,
又∵两个人之间握手的次数只能算作一次,
∴最后握手的总次数次;
∴若有个人,一共要握次手.
21.
解:由AC=8cm,N是AC的中点,得
AN= AC=4cm.
由线段的和差,得
AM=AN+MN=4+6=10cm.
由M是线段AB的中点,得
AB=2AM=20cm,
线段AB的长是20cm.
22.
解:将圆柱体展开为平面图形如图所示:
∴蚂蚁在A处,想到C处的最短路线如图所示,
理由是:两点之间,线段最短.
23.
解:(1)图如所示:
线段有:AC、AD、AE、AB、CD、CE、CB、DE、DB、EB,
线段的条数:4+3+2+1=10(条);
(2)如图,如果在线段CD上增加一点P,则P与其它五个点各组成一条线段,
分别是:PA、PC、PD、PE、PB,
∴增加了5条线段.
规律:若在线段AB上增加一点,则增加2条线段,此时线段总条数为1+2;
若再增加一点,则又增加了3条线段,此时线段总条数为1+2+3;…;
当线段AB上增加到n个点(即增加n-2个点)时,线段的总条数为:
1+2+……+(n-1)=n(n-1) .
24.
解:(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
一、选择题(本大题共12小题,每小题3分,共36分。)
1.当分针指向12,时针这时恰好与分针成30°的角,此时是( )
A.9点钟 B.10点钟 C.11点钟或1点钟 D.2点钟或10点钟
2.下列说法正确的是( )
A.角的大小和开口的大小无关 B.互余、互补是指两个角之间的数量关系
C.单独的一个角也可以叫余角或补角 D.若三个角的和是直角,则他们互余
3.根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )
A. B.
C. D.
4.下列各图中直线的表示法正确的是( ).
A. B.
C. D.
5.下列说法正确的是( ).
A.两点之间的距离是两点间的直线长度
B.两点之间,射线最短
C.经过三点,只有一条直线
D.同角的余角相等
6.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
7.如图,O为我国南海某人造海岛,某国商船在A的位置,∠1=40°,下列说法正确的是( )
A.商船在海岛的北偏西50°方向 B.海岛在商船的北偏西40°方向
C.海岛在商船的东偏南50°方向 D.商船在海岛的东偏南40°方向
8.下图中,能用∠ABC,∠B,∠1三种方法表示同一个角的图形是( )
A. B.
C. D.
9.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
A.45° B.55° C.65° D.75
10.数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2020厘米的线段AB,则线段AB盖住的整点个数是( )
A.2018或2019 B.2019或2020 C.2020或2021 D.2021或2022
11.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠BOC=30°,则∠AOD等于( )
A.10° B.150° C.140° D.160°
12.李刚同学设计了四种正多边形的瓷砖图案,在这四种瓷砖中,用一种瓷砖可以密铺平面的是( )
A.(1)(2)(4) B.(2)(3)(4)
C.(1)(3)(4) D.(1)(2)(3)
二、填空题(本大题共6小题,每小题3分,共18分)
13.如图,AB=6,BC=4,D、E分别是AB、BC的中点,则BD+BE=_____,根据公理:_______________,可知BD+BE_____DE.
14.在直线l上顺次取A、B、C三点,使得AB=3cm,BC=5cm,若点D是线段AC的中点,则线段DB的长度等于__cm.
15.如图所示,OD、OE是两条射线,A在射线OD上,B、C在射线OE上,则图有共有线段________条,分别是________;共有________条射线,分别是________.
16.已知线段AB=7cm,在直线AB上画线段BC,使它等于3cm,则线段AC=____cm.
17.书店、学校、食堂在同一个平面上,分别用点A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC应该是______________.
18.如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB=_______.
三、解答题(本大题共6小题,共66分,解答应写出文字说明、演算步骤或推理过程)
19.已知:如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若线段AC=6,BC=4,求线段MN的长度;
(2)若AB=a,求线段MN的长度;
(3)若将(1)小题中“点C在线段AB上”改为“点C在直线AB上”,(1)小题的结果会有变化吗 求出MN的长度.
20.小明发现这样一个问题:“在一次聚会中,共有6人参加,如果每两人都握一次手,共握几次手 ”通过思考,小明得出了答案, 那请问同学们:如果有n个人参加聚会,每两人都握一次手,一共要握多少次手呢
21.如图,M是线段AB的中点,点C在线段AB上,且AC=8cm,N是AC的中点,MN=6cm,求线段AB的长.
22.如图所示一只蚂蚁在A处,想到C处的最短路线,请画出简图,并说明理由.
23.已知线段AB上有三个定点C、D、E.
(1)图中共有几条线段?
(2)如果在线段CD上增加一点,则增加了几条线段?你能从中发现什么规律吗?
24.读下列语句,并分别画出图形:
(1)直线l经过A、B、C三点,点C在点A与点B之间;
(2)两条直线m与n相交于点P;
(3)线段a、b相交于点O,与线段c分别交于点P、Q.
答案
一、选择题
C.B.C.C.D.D.B.D.B.C.B.A.
二、填空题
13.5 两点之间线段最短 >
14.1
15.6 线段OA、OB、OC、BC、AC、AB 5 射线OD、OE、BE、AD、CE
16.10或4或4
17.165°
18.20°
三、解答题
19.
解:(1)∵ AC=6,BC=4,
∴ AB=6+4=10,
又∵ 点M是AC的中点,点N是BC的中点,
∴ MC=AM=AC,CN=BN=BC,
∴ MN=MC+CN=AC+BC=(AC+BC)=AB=5(cm).
(2)由(1)中已知AB=10cm求出MN=5cm,分析(1)的推算过程可知MN=AB,
故当AB=a时,MN=,
从而得到规律:线段上任一点把线段分成的两部分的中点间的距离等于原线段长度的一半.
(3)分类讨论:
当点C在点B的右侧时,如图可得:
;
当点C在线段AB上时,如(1);
当点C在点A的左侧时,不满足题意.
综上可得:点C在直线AB上时,MN的长为1或5.
20.
解:∵若有6个人参加聚会,则每个人都要与另外5个人握手一次,
∴一共要握手次,
又∵两个人之间握手的次数只能算作一次,
∴最后握手的总次数次;
∵若有n个人参加聚会,则每个人都要与另外n-1个人握手一次,
∴一共要握手次,
又∵两个人之间握手的次数只能算作一次,
∴最后握手的总次数次;
∴若有个人,一共要握次手.
21.
解:由AC=8cm,N是AC的中点,得
AN= AC=4cm.
由线段的和差,得
AM=AN+MN=4+6=10cm.
由M是线段AB的中点,得
AB=2AM=20cm,
线段AB的长是20cm.
22.
解:将圆柱体展开为平面图形如图所示:
∴蚂蚁在A处,想到C处的最短路线如图所示,
理由是:两点之间,线段最短.
23.
解:(1)图如所示:
线段有:AC、AD、AE、AB、CD、CE、CB、DE、DB、EB,
线段的条数:4+3+2+1=10(条);
(2)如图,如果在线段CD上增加一点P,则P与其它五个点各组成一条线段,
分别是:PA、PC、PD、PE、PB,
∴增加了5条线段.
规律:若在线段AB上增加一点,则增加2条线段,此时线段总条数为1+2;
若再增加一点,则又增加了3条线段,此时线段总条数为1+2+3;…;
当线段AB上增加到n个点(即增加n-2个点)时,线段的总条数为:
1+2+……+(n-1)=n(n-1) .
24.
解:(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
