七年级数学上册试题 第6章 《数据的收集与整理》单元测试卷-北师大版(含答案)
文档属性
| 名称 | 七年级数学上册试题 第6章 《数据的收集与整理》单元测试卷-北师大版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 888.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 00:00:00 | ||
图片预览


文档简介
第6章 《数据的收集与整理》单元测试卷
一、单选题(每题3分,共30分)
1.调查下面的问题,应该进行全面调查的是( )
A.市场上某种食品的色素是否符合国家标准 B.某单位所有人员的住房情况
C.一个城市某一天的空气质量 D.某款品牌手机的触摸屏寿命
2.下列调查中适合用查阅资料的方法收集数据的是( )
A.2018足球世界杯中,进球最多的队员 B.本校学生的到校时间
C.班级推选班长 D.本班同学最喜欢的明星
3.某次考试有3000名学生参加,为了了解3000名学生的数学成绩,从中抽取了1000名学生的数学成绩进行调查统计分析,在这个问题中,有下述3种说法:①1000名考生是总体的一个样本;②3000名考生是总体;③1000名考生数学平均成绩可估计总体数学平均成绩;④每个考生的数学成绩是个体.其中正确的说法有( )
A.0种 B.1种 C.2种 D.3种
4.如图,是某家庭第一季度用电量的扇形统计图,则三月份用电量占第一季度用电量的百分比是( )
A.65% B.75% C.85% D.95%
5.要反映2010年至2019年华容县学生人数的变化情况,应绘制( )
A.复式统计图 B.条形统计图 C.扇形统计图 D.折线统计图
6.在“5 18世界无烟日”来临之际,小明和他的同学为了解某街道大约有多少成年人吸烟,于是随机调查了该街道1000个成年人,结果有180个成年人吸烟.对于这个数据的收集与处理过程,下列说法正确的是( )
A.调查的方式是普查
B.该街道约有18%的成年人吸烟
C.该街道只有820个成年人不吸烟
D.样本是180个吸烟的成年人
7.已知数据35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34,在列频数分布表时,如果取组距为2,那么应分成组数为( )
A.4 B.5 C.6 D.7
8.浣江初中创办于1991年8月,坐落在西施故里浣江之滨,现有58个班级,3000余名师生,是全市规模最大的直属初中,“深耕志远”是学校的核心文化,其中58个班级中的58属于( )
A.计数 B.测量 C.标号 D.排序
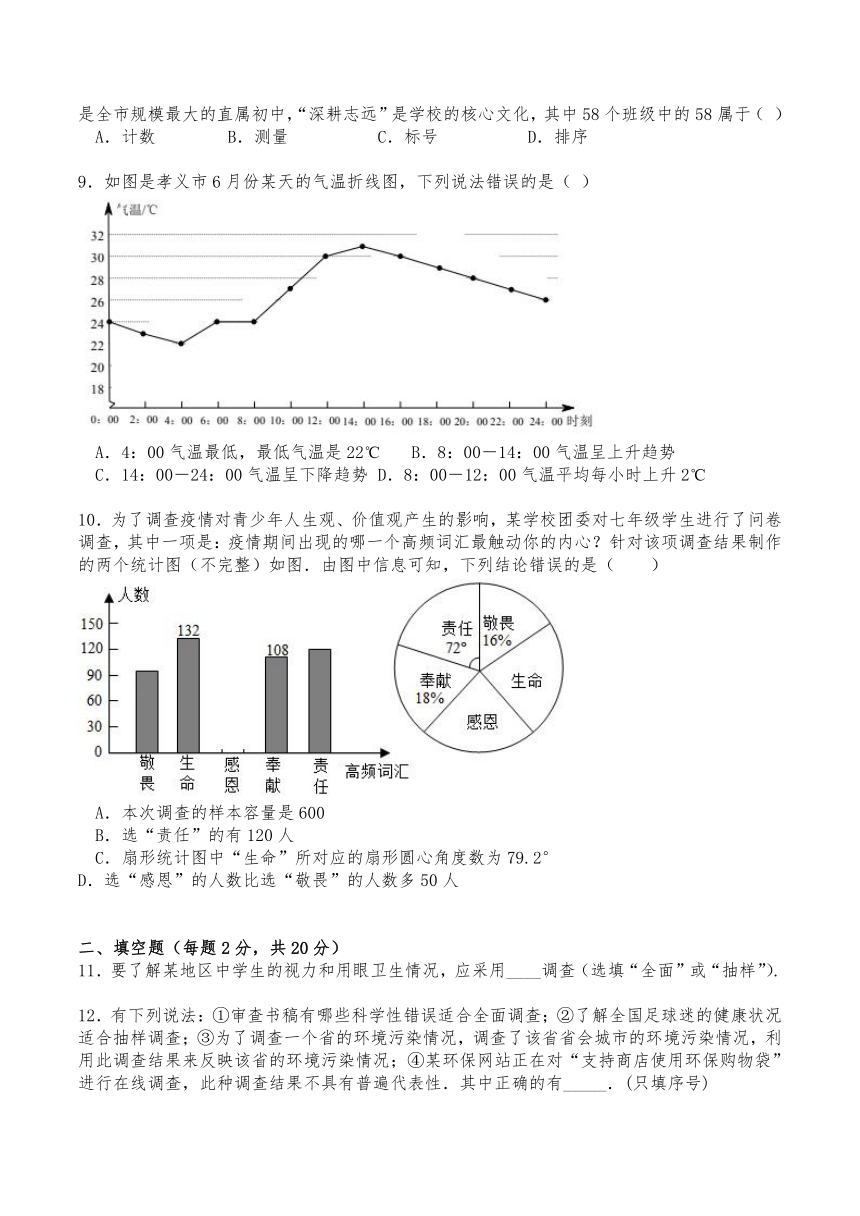
9.如图是孝义市6月份某天的气温折线图,下列说法错误的是( )
A.4:00气温最低,最低气温是22℃ B.8:00-14:00气温呈上升趋势
C.14:00-24:00气温呈下降趋势 D.8:00-12:00气温平均每小时上升2℃
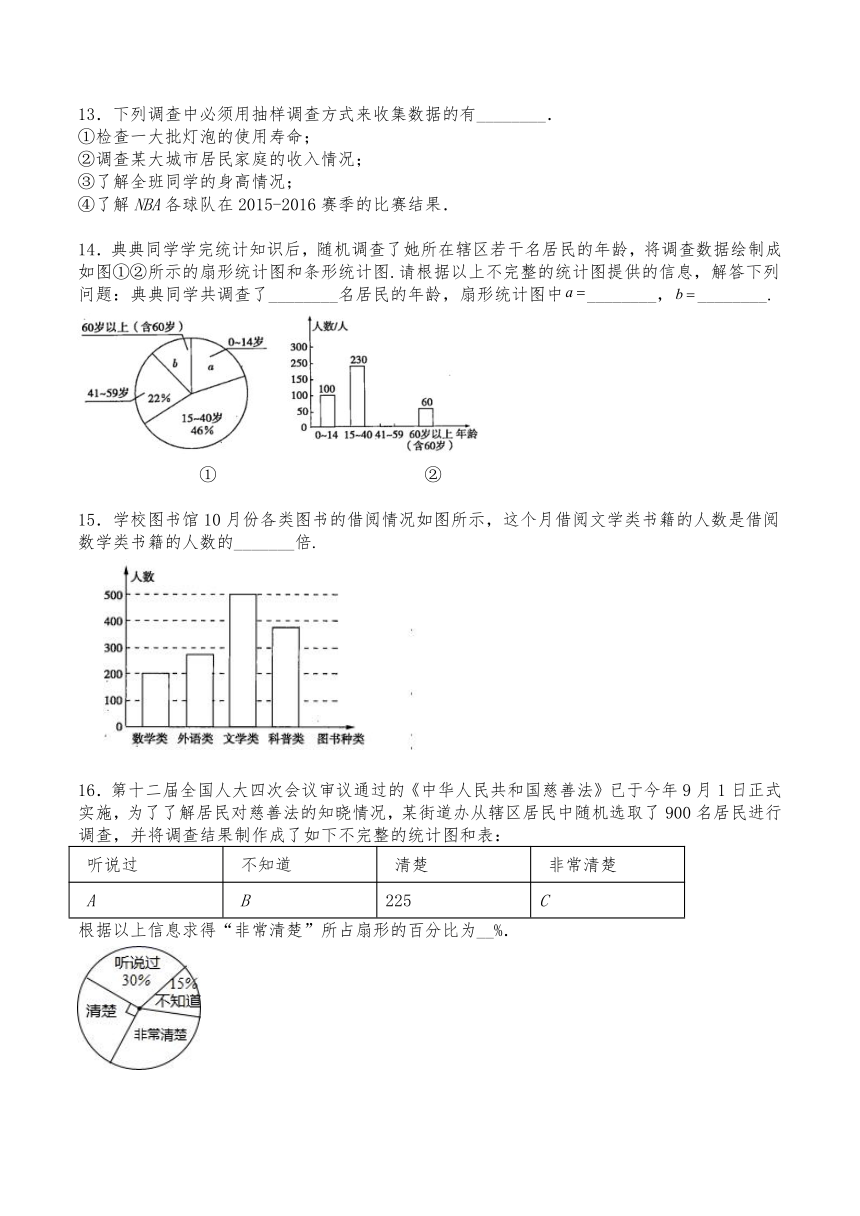
10.为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对七年级学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图.由图中信息可知,下列结论错误的是( )
A.本次调查的样本容量是600
B.选“责任”的有120人
C.扇形统计图中“生命”所对应的扇形圆心角度数为79.2°
D.选“感恩”的人数比选“敬畏”的人数多50人
二、填空题(每题2分,共20分)
11.要了解某地区中学生的视力和用眼卫生情况,应采用____调查(选填“全面”或“抽样”).
12.有下列说法:①审查书稿有哪些科学性错误适合全面调查;②了解全国足球迷的健康状况适合抽样调查;③为了调查一个省的环境污染情况,调查了该省省会城市的环境污染情况,利用此调查结果来反映该省的环境污染情况;④某环保网站正在对“支持商店使用环保购物袋”进行在线调查,此种调查结果不具有普遍代表性.其中正确的有_____.(只填序号)
13.下列调查中必须用抽样调查方式来收集数据的有________.
①检查一大批灯泡的使用寿命;
②调查某大城市居民家庭的收入情况;
③了解全班同学的身高情况;
④了解NBA各球队在2015-2016赛季的比赛结果.
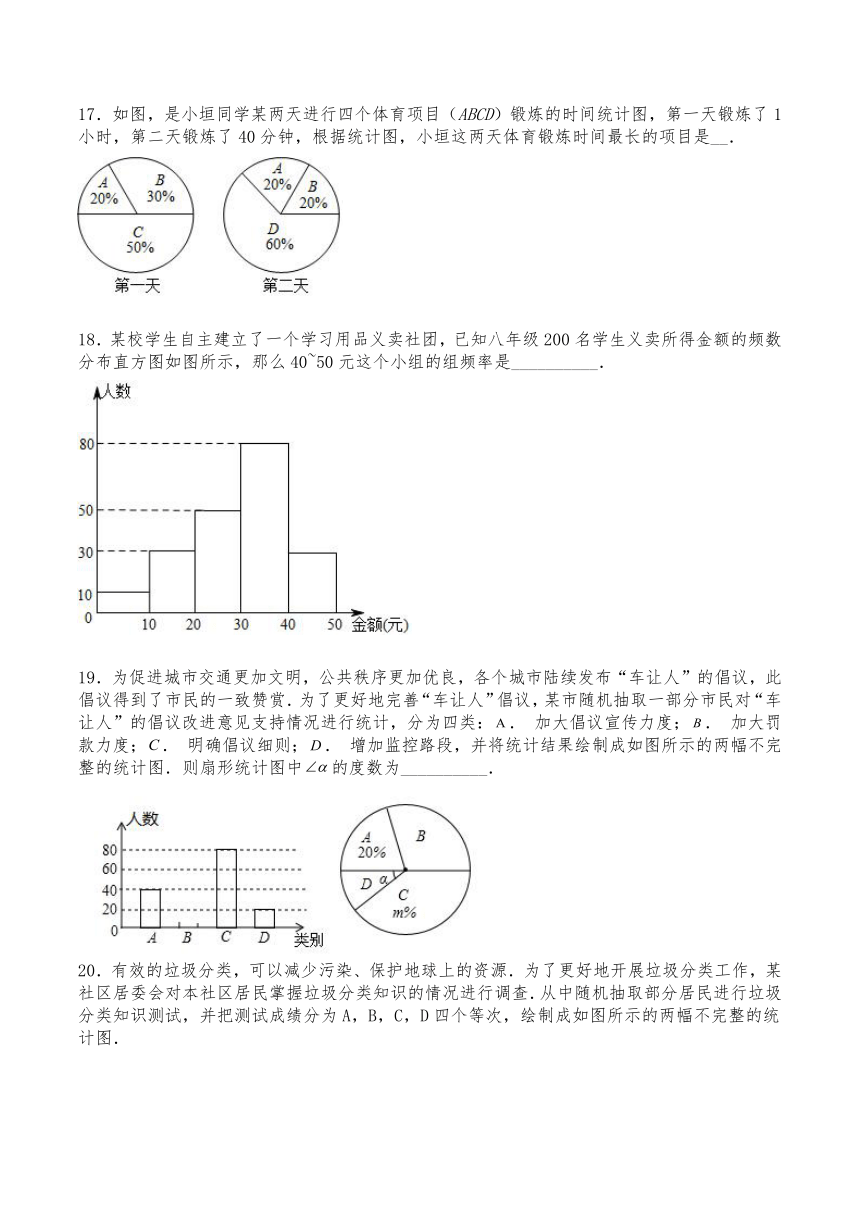
14.典典同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如图①②所示的扇形统计图和条形统计图.请根据以上不完整的统计图提供的信息,解答下列问题:典典同学共调查了________名居民的年龄,扇形统计图中________,________.
① ②
15.学校图书馆10月份各类图书的借阅情况如图所示,这个月借阅文学类书籍的人数是借阅数学类书籍的人数的_______倍.
16.第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了900名居民进行调查,并将调查结果制作成了如下不完整的统计图和表:
听说过 不知道 清楚 非常清楚
A B 225 C
根据以上信息求得“非常清楚”所占扇形的百分比为__%.
17.如图,是小垣同学某两天进行四个体育项目(ABCD)锻炼的时间统计图,第一天锻炼了1小时,第二天锻炼了40分钟,根据统计图,小垣这两天体育锻炼时间最长的项目是__.
18.某校学生自主建立了一个学习用品义卖社团,已知八年级200名学生义卖所得金额的频数分布直方图如图所示,那么40~50元这个小组的组频率是__________.
19.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取一部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:. 加大倡议宣传力度;. 加大罚款力度;. 明确倡议细则;. 增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中的度数为__________.
20.有效的垃圾分类,可以减少污染、保护地球上的资源.为了更好地开展垃圾分类工作,某社区居委会对本社区居民掌握垃圾分类知识的情况进行调查.从中随机抽取部分居民进行垃圾分类知识测试,并把测试成绩分为A,B,C,D四个等次,绘制成如图所示的两幅不完整的统计图.
下面有四个推断:
①本次的调查方式是抽样调查,样本容量是40;
②扇形统计图中,表示C等次的扇形的圆心角的度数为72°;
③测试成绩为D等次的居民人数占参测总人数的10%;
④测试成绩为A或B等次的居民人数共30人.
所有合理推断的序号是______.
三、解答题(50分)
(6分)21.为了完成下列任务,你认为可采用什么调查方式?
(1)了解全国八年级学生的体重,掌握学生的身体发育情况;
(2)考察一批炮弹的杀伤半径;
(3)了解本班同学每周的睡眠时间;
(4)为了体现公平的体育精神,关爱运动员的身心健康,国际奥委会明令禁止运动员服用违禁药物.为了了解奥运会上运动员的执行情况,对运动员进行的尿样检查.
(6分)22.为了了解你们学校的学生是否吃早饭,下列这些抽取样本的方式是否合适?
(1)早上7:00至7:30在校门口随机选择50名同学进行调查;
(2)选择全校每个班级中学号是5和15的同学进行调查;
(3)选择七(1)班全体学生进行调查.
(6分)23.甲、乙两公司近年的赢利情况如图所示.
(1)哪家公司近年利润的增长速度较快?
(2)统计图给你的感觉和上述结果一样吗?如果不一样,你知道其中的原因吗?
(6分)24.为了调查居民的生活水平,有关部门对某个地区5个街道的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.6 3.5 2.3 6.5 2.2 1.9 6.8 4.8 5.0 4.7 2.3
1.5 3.1 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8 3.0
5.1 7.0 3.1 2.9 4.4 5.8 3.8 3.7 3.3 5.2 4.1
4.2 4.8 3.0 4.0 4.6 6.0 2.4 3.3 6.1 5.0 4.9
3.0 3.1 7.2 1.8 5.0 1.9
将数据适当分组,并绘制相应的频数直方图.
(6分)25.某市发布了一份空气质量抽样调查报告,在该市1~5月随机调查的30天中,各空气质量级别的天数如下图:
(1)请在所给条形图右侧绘制扇形图,描述这30天中不同空气质量级别的天数所占的百分比情况.
(2)通过分析扇形图,请你评价一下1~5月份该市的空气质量情况._______________.
(3)如果这30天的数据是从一年中随机抽取的,请你预测该市一年(365天)空气质量级别为优和良的天数共约有多少天?(结果保留整数)
(4)请你根据调查报告,对有关部门提几条建设“绿色环境城市”的建议.
(6分)26.小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).
分组 频数 频率
600~799 2 0.050
800~999 6 0.150
1000~1199 0.450
1200~1399 9 0.225
1400~1599
1600~1800 2 0.050
合计 40 1.000
根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图.
(2)观察已绘制的部分频数分布直方图,你能看出绘制选择的组距是多少吗?这个组距选择得好不好?请判断并说明理由._____________________.
(3)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户.
(7分)27.下面数据是截至2010年费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35
31 31 37 32 38 36 31 39
32 38 37 34 29 34 38 32
35 36 33 29 32 35 3.6 37
39 38 40 38 37 39 38 34
33 40 36 36 37 40 31 38
38 40 40 37
请根据下面不同的分组方法列出频数分布表,画出频数分布直方图,比较哪一种分组能更好地说明费尔兹奖得主获奖时的年龄分布:
(1)组距是2,各组是,,…;
(2)组距是5,各组是,,…;
(3)组距是10,各组是,,….
(7分)28.为了增强学生的疫情防控意识,响应“停课不停学”号召,某学校组织了一次疫情防控知识专题网上学习,并进行了一次全校名学生都参加的网上测试,阅卷后,教务处随机抽取收了份答卷进行分析统计,发现考试成绩(分)的最低分为分,最高分为满分分,并绘制了尚不完整的统计图表,请根据图表提供的信息,解答下列问题:
分数段(分) 频数(人) 频率
合计
(1)填空:______,______,______;
(2)将频数分布直方图补充完整;
(3)在绘制扇形统计图中,这一分数段所占的圆心角度数为______°;
(4)该校对成绩为的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为,请你估算全校获得二等奖的学生人数.
答案
一、单选题
B.A.C.A.D.B.B.A.D.D.
二、填空题
11.抽样
12.①②④
13.①②
14.500, 20%, 12%
15.2.5
16.30
17.C
18.0.15
19.
20.①②④
三、解答题
21.
(1)采用抽样调查;因为总体的数量太多,无法一一调查.
(2)采用抽样调查;因为这种调查具有破坏性.
(3)采用普查.个体数量不是太多,这样更能得到准确的数据.
(4)采用普查.因为这里要求准确了解每一位运动员的执行情况.
22.
(1)符合样本抽取的代表性,广泛性,全面性的特点,
故可以;
(2)符合样本抽取的代表性,广泛性,全面性的特点,
故可以;
(3)不符合样本抽取的代表性,广泛性,全面性的特点,
故不可以.
23.
解:(1)从2004-2010年甲公司利润由40万元增长到130万元,
乙公司利润由40万元增长到90万元,
所以甲公司近年利润的增长速度较快;
(2)统计图给人的感觉和上述结果不一样,
这是因为两幅图中坐标轴上同一单位长度表示的意义不一致,
图(甲)中140万元的利润看起来与图(乙)中100万元相当,
而图(甲)中表示一年的间隔长度要大于图(乙)中表示一年的间隔长度.
也就是说,图(甲)与图(乙)相比,纵轴(利润)被“压缩”了,
横轴(年份)被“拉长”了,
结果使得图(甲)的折线看起来更“缓”了.
24.
解:第一步,计算最大值与最小值的差:
在所给的数据中,最大值是7.2,最小值是1.5,
它们的差是7.2-1.5=5.7,
第二步,决定组距与组数:
由于最大值与最小值的差是5.7,
如果取组距为1,那么由于,可分成6组,
组数合适,于是取组距为1,组数为6,
第三步,列频数分布表:
分组 频数
10
10
11
10
5
4
合计 50
第四步,画频数直方图:
25.
(1)由条形统计图可得,
空气质量为优,所占百分比为:,所在的扇形的圆心角为:
空气质量为良,所占百分比为:,所在的扇形的圆心角为
空气质量为轻微污染,所占百分比为:,所在的扇形的圆心角为:
空气质量为轻度污染,所占百分比为:,所在的扇形的圆心角为:
空气质量为中度污染,所占百分比为:,所在的扇形的圆心角为:
绘制扇形统计图如图所示,
(2)该市1~5月的空气质量级别主要是良及以上,
故答案为:空气质量级别主要是良及以上.
(3),该市1年空气质量为优和良级别的天数共约为243.
(4)建议:加大空气污染治理力度,提高空气质量等级为“优”的天数,努力减少轻度污染、中度污染的天数.(只要提出改善该市空气质量状况的合理建议即可).
26.
解:(1)∵在1000~1199组中,调查了40户居民家庭,频率为0.450,
∴频数为0.450×40=18,
在1400~1599组中,
频数=40-2-6-18-9-2=40-37=3,
频率=1-0.050-0.150-0.450-0.225-0.050=0.075,
完成表格如下,
分组 频数 频率
600~799 2 0.050
800~999 6 0.150
1000~1199 18 0.450
1200~1399 9 0.225
1400~1599 3 0.075
1600~1800 2 0.050
合计 40 1.000
补全频率直方图如下
(2)组距为200.
∵极差为1800-600=1200元,分6组,每组的组距为1200÷6=200元,
∴这个组距选择比较合理,确保了数据的不重不漏,把右分点的收入整百的户数分在下一组,且没有数据为空白的组比较好地展示了数据的分布情况.
(3)∵家庭人均月收入“大于等于1000不足1600元”的为中等收入家庭有18+9+3=30,
占样本的百分比为30÷40×100%=75%,
440户居民的家庭总体中的中等收入家庭大约有440×75%=330户.
27.
(1)根据所给数据整理得出,
范围 28≤x<30 30≤x<32 32≤x<34 34≤x<36 36≤x<38 38≤x<40 40≤x<42
人数 4 4 8 7 11 13 5
(2)根据所给数据整理得出,
范围 25≤x<30 30≤x<35 35≤x<40 40≤x<45
人数 4 15 28 5
根据所给数据整理得出,
(3)根据所给数据整理得出,
范围 20≤x<30 30≤x<40 40≤x<50
人数 4 43 5
以上为三组图表和分布图,(1)组组距为2过于小,将数据分为7个组,组数过多,比较起来比较繁琐;(3)组组距为10过于大,将数据分为3个组,组数过少比较起来参考性小;所以(2)组更能说明诺贝尔奖者年龄分布情况.
28.
解:(1)a=100×0.1=10,
b=100-10-18-35-12=25,
n=25÷100=0.25.
故答案为:10,25,0.25;
(2)如图,即为补充完整的频数分布直方图;
(3)81≤x<91这一分数段所占的圆心角度数为360×0.35=126°;
故答案为:126;
(4)∵2500××=90(人)
∴估算全校获得二等奖的学生人数为90人.
一、单选题(每题3分,共30分)
1.调查下面的问题,应该进行全面调查的是( )
A.市场上某种食品的色素是否符合国家标准 B.某单位所有人员的住房情况
C.一个城市某一天的空气质量 D.某款品牌手机的触摸屏寿命
2.下列调查中适合用查阅资料的方法收集数据的是( )
A.2018足球世界杯中,进球最多的队员 B.本校学生的到校时间
C.班级推选班长 D.本班同学最喜欢的明星
3.某次考试有3000名学生参加,为了了解3000名学生的数学成绩,从中抽取了1000名学生的数学成绩进行调查统计分析,在这个问题中,有下述3种说法:①1000名考生是总体的一个样本;②3000名考生是总体;③1000名考生数学平均成绩可估计总体数学平均成绩;④每个考生的数学成绩是个体.其中正确的说法有( )
A.0种 B.1种 C.2种 D.3种
4.如图,是某家庭第一季度用电量的扇形统计图,则三月份用电量占第一季度用电量的百分比是( )
A.65% B.75% C.85% D.95%
5.要反映2010年至2019年华容县学生人数的变化情况,应绘制( )
A.复式统计图 B.条形统计图 C.扇形统计图 D.折线统计图
6.在“5 18世界无烟日”来临之际,小明和他的同学为了解某街道大约有多少成年人吸烟,于是随机调查了该街道1000个成年人,结果有180个成年人吸烟.对于这个数据的收集与处理过程,下列说法正确的是( )
A.调查的方式是普查
B.该街道约有18%的成年人吸烟
C.该街道只有820个成年人不吸烟
D.样本是180个吸烟的成年人
7.已知数据35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34,在列频数分布表时,如果取组距为2,那么应分成组数为( )
A.4 B.5 C.6 D.7
8.浣江初中创办于1991年8月,坐落在西施故里浣江之滨,现有58个班级,3000余名师生,是全市规模最大的直属初中,“深耕志远”是学校的核心文化,其中58个班级中的58属于( )
A.计数 B.测量 C.标号 D.排序
9.如图是孝义市6月份某天的气温折线图,下列说法错误的是( )
A.4:00气温最低,最低气温是22℃ B.8:00-14:00气温呈上升趋势
C.14:00-24:00气温呈下降趋势 D.8:00-12:00气温平均每小时上升2℃
10.为了调查疫情对青少年人生观、价值观产生的影响,某学校团委对七年级学生进行了问卷调查,其中一项是:疫情期间出现的哪一个高频词汇最触动你的内心?针对该项调查结果制作的两个统计图(不完整)如图.由图中信息可知,下列结论错误的是( )
A.本次调查的样本容量是600
B.选“责任”的有120人
C.扇形统计图中“生命”所对应的扇形圆心角度数为79.2°
D.选“感恩”的人数比选“敬畏”的人数多50人
二、填空题(每题2分,共20分)
11.要了解某地区中学生的视力和用眼卫生情况,应采用____调查(选填“全面”或“抽样”).
12.有下列说法:①审查书稿有哪些科学性错误适合全面调查;②了解全国足球迷的健康状况适合抽样调查;③为了调查一个省的环境污染情况,调查了该省省会城市的环境污染情况,利用此调查结果来反映该省的环境污染情况;④某环保网站正在对“支持商店使用环保购物袋”进行在线调查,此种调查结果不具有普遍代表性.其中正确的有_____.(只填序号)
13.下列调查中必须用抽样调查方式来收集数据的有________.
①检查一大批灯泡的使用寿命;
②调查某大城市居民家庭的收入情况;
③了解全班同学的身高情况;
④了解NBA各球队在2015-2016赛季的比赛结果.
14.典典同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如图①②所示的扇形统计图和条形统计图.请根据以上不完整的统计图提供的信息,解答下列问题:典典同学共调查了________名居民的年龄,扇形统计图中________,________.
① ②
15.学校图书馆10月份各类图书的借阅情况如图所示,这个月借阅文学类书籍的人数是借阅数学类书籍的人数的_______倍.
16.第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了900名居民进行调查,并将调查结果制作成了如下不完整的统计图和表:
听说过 不知道 清楚 非常清楚
A B 225 C
根据以上信息求得“非常清楚”所占扇形的百分比为__%.
17.如图,是小垣同学某两天进行四个体育项目(ABCD)锻炼的时间统计图,第一天锻炼了1小时,第二天锻炼了40分钟,根据统计图,小垣这两天体育锻炼时间最长的项目是__.
18.某校学生自主建立了一个学习用品义卖社团,已知八年级200名学生义卖所得金额的频数分布直方图如图所示,那么40~50元这个小组的组频率是__________.
19.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取一部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:. 加大倡议宣传力度;. 加大罚款力度;. 明确倡议细则;. 增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中的度数为__________.
20.有效的垃圾分类,可以减少污染、保护地球上的资源.为了更好地开展垃圾分类工作,某社区居委会对本社区居民掌握垃圾分类知识的情况进行调查.从中随机抽取部分居民进行垃圾分类知识测试,并把测试成绩分为A,B,C,D四个等次,绘制成如图所示的两幅不完整的统计图.
下面有四个推断:
①本次的调查方式是抽样调查,样本容量是40;
②扇形统计图中,表示C等次的扇形的圆心角的度数为72°;
③测试成绩为D等次的居民人数占参测总人数的10%;
④测试成绩为A或B等次的居民人数共30人.
所有合理推断的序号是______.
三、解答题(50分)
(6分)21.为了完成下列任务,你认为可采用什么调查方式?
(1)了解全国八年级学生的体重,掌握学生的身体发育情况;
(2)考察一批炮弹的杀伤半径;
(3)了解本班同学每周的睡眠时间;
(4)为了体现公平的体育精神,关爱运动员的身心健康,国际奥委会明令禁止运动员服用违禁药物.为了了解奥运会上运动员的执行情况,对运动员进行的尿样检查.
(6分)22.为了了解你们学校的学生是否吃早饭,下列这些抽取样本的方式是否合适?
(1)早上7:00至7:30在校门口随机选择50名同学进行调查;
(2)选择全校每个班级中学号是5和15的同学进行调查;
(3)选择七(1)班全体学生进行调查.
(6分)23.甲、乙两公司近年的赢利情况如图所示.
(1)哪家公司近年利润的增长速度较快?
(2)统计图给你的感觉和上述结果一样吗?如果不一样,你知道其中的原因吗?
(6分)24.为了调查居民的生活水平,有关部门对某个地区5个街道的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.6 3.5 2.3 6.5 2.2 1.9 6.8 4.8 5.0 4.7 2.3
1.5 3.1 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8 3.0
5.1 7.0 3.1 2.9 4.4 5.8 3.8 3.7 3.3 5.2 4.1
4.2 4.8 3.0 4.0 4.6 6.0 2.4 3.3 6.1 5.0 4.9
3.0 3.1 7.2 1.8 5.0 1.9
将数据适当分组,并绘制相应的频数直方图.
(6分)25.某市发布了一份空气质量抽样调查报告,在该市1~5月随机调查的30天中,各空气质量级别的天数如下图:
(1)请在所给条形图右侧绘制扇形图,描述这30天中不同空气质量级别的天数所占的百分比情况.
(2)通过分析扇形图,请你评价一下1~5月份该市的空气质量情况._______________.
(3)如果这30天的数据是从一年中随机抽取的,请你预测该市一年(365天)空气质量级别为优和良的天数共约有多少天?(结果保留整数)
(4)请你根据调查报告,对有关部门提几条建设“绿色环境城市”的建议.
(6分)26.小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).
分组 频数 频率
600~799 2 0.050
800~999 6 0.150
1000~1199 0.450
1200~1399 9 0.225
1400~1599
1600~1800 2 0.050
合计 40 1.000
根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图.
(2)观察已绘制的部分频数分布直方图,你能看出绘制选择的组距是多少吗?这个组距选择得好不好?请判断并说明理由._____________________.
(3)如果家庭人均月收入“大于1000不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户.
(7分)27.下面数据是截至2010年费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35
31 31 37 32 38 36 31 39
32 38 37 34 29 34 38 32
35 36 33 29 32 35 3.6 37
39 38 40 38 37 39 38 34
33 40 36 36 37 40 31 38
38 40 40 37
请根据下面不同的分组方法列出频数分布表,画出频数分布直方图,比较哪一种分组能更好地说明费尔兹奖得主获奖时的年龄分布:
(1)组距是2,各组是,,…;
(2)组距是5,各组是,,…;
(3)组距是10,各组是,,….
(7分)28.为了增强学生的疫情防控意识,响应“停课不停学”号召,某学校组织了一次疫情防控知识专题网上学习,并进行了一次全校名学生都参加的网上测试,阅卷后,教务处随机抽取收了份答卷进行分析统计,发现考试成绩(分)的最低分为分,最高分为满分分,并绘制了尚不完整的统计图表,请根据图表提供的信息,解答下列问题:
分数段(分) 频数(人) 频率
合计
(1)填空:______,______,______;
(2)将频数分布直方图补充完整;
(3)在绘制扇形统计图中,这一分数段所占的圆心角度数为______°;
(4)该校对成绩为的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为,请你估算全校获得二等奖的学生人数.
答案
一、单选题
B.A.C.A.D.B.B.A.D.D.
二、填空题
11.抽样
12.①②④
13.①②
14.500, 20%, 12%
15.2.5
16.30
17.C
18.0.15
19.
20.①②④
三、解答题
21.
(1)采用抽样调查;因为总体的数量太多,无法一一调查.
(2)采用抽样调查;因为这种调查具有破坏性.
(3)采用普查.个体数量不是太多,这样更能得到准确的数据.
(4)采用普查.因为这里要求准确了解每一位运动员的执行情况.
22.
(1)符合样本抽取的代表性,广泛性,全面性的特点,
故可以;
(2)符合样本抽取的代表性,广泛性,全面性的特点,
故可以;
(3)不符合样本抽取的代表性,广泛性,全面性的特点,
故不可以.
23.
解:(1)从2004-2010年甲公司利润由40万元增长到130万元,
乙公司利润由40万元增长到90万元,
所以甲公司近年利润的增长速度较快;
(2)统计图给人的感觉和上述结果不一样,
这是因为两幅图中坐标轴上同一单位长度表示的意义不一致,
图(甲)中140万元的利润看起来与图(乙)中100万元相当,
而图(甲)中表示一年的间隔长度要大于图(乙)中表示一年的间隔长度.
也就是说,图(甲)与图(乙)相比,纵轴(利润)被“压缩”了,
横轴(年份)被“拉长”了,
结果使得图(甲)的折线看起来更“缓”了.
24.
解:第一步,计算最大值与最小值的差:
在所给的数据中,最大值是7.2,最小值是1.5,
它们的差是7.2-1.5=5.7,
第二步,决定组距与组数:
由于最大值与最小值的差是5.7,
如果取组距为1,那么由于,可分成6组,
组数合适,于是取组距为1,组数为6,
第三步,列频数分布表:
分组 频数
10
10
11
10
5
4
合计 50
第四步,画频数直方图:
25.
(1)由条形统计图可得,
空气质量为优,所占百分比为:,所在的扇形的圆心角为:
空气质量为良,所占百分比为:,所在的扇形的圆心角为
空气质量为轻微污染,所占百分比为:,所在的扇形的圆心角为:
空气质量为轻度污染,所占百分比为:,所在的扇形的圆心角为:
空气质量为中度污染,所占百分比为:,所在的扇形的圆心角为:
绘制扇形统计图如图所示,
(2)该市1~5月的空气质量级别主要是良及以上,
故答案为:空气质量级别主要是良及以上.
(3),该市1年空气质量为优和良级别的天数共约为243.
(4)建议:加大空气污染治理力度,提高空气质量等级为“优”的天数,努力减少轻度污染、中度污染的天数.(只要提出改善该市空气质量状况的合理建议即可).
26.
解:(1)∵在1000~1199组中,调查了40户居民家庭,频率为0.450,
∴频数为0.450×40=18,
在1400~1599组中,
频数=40-2-6-18-9-2=40-37=3,
频率=1-0.050-0.150-0.450-0.225-0.050=0.075,
完成表格如下,
分组 频数 频率
600~799 2 0.050
800~999 6 0.150
1000~1199 18 0.450
1200~1399 9 0.225
1400~1599 3 0.075
1600~1800 2 0.050
合计 40 1.000
补全频率直方图如下
(2)组距为200.
∵极差为1800-600=1200元,分6组,每组的组距为1200÷6=200元,
∴这个组距选择比较合理,确保了数据的不重不漏,把右分点的收入整百的户数分在下一组,且没有数据为空白的组比较好地展示了数据的分布情况.
(3)∵家庭人均月收入“大于等于1000不足1600元”的为中等收入家庭有18+9+3=30,
占样本的百分比为30÷40×100%=75%,
440户居民的家庭总体中的中等收入家庭大约有440×75%=330户.
27.
(1)根据所给数据整理得出,
范围 28≤x<30 30≤x<32 32≤x<34 34≤x<36 36≤x<38 38≤x<40 40≤x<42
人数 4 4 8 7 11 13 5
(2)根据所给数据整理得出,
范围 25≤x<30 30≤x<35 35≤x<40 40≤x<45
人数 4 15 28 5
根据所给数据整理得出,
(3)根据所给数据整理得出,
范围 20≤x<30 30≤x<40 40≤x<50
人数 4 43 5
以上为三组图表和分布图,(1)组组距为2过于小,将数据分为7个组,组数过多,比较起来比较繁琐;(3)组组距为10过于大,将数据分为3个组,组数过少比较起来参考性小;所以(2)组更能说明诺贝尔奖者年龄分布情况.
28.
解:(1)a=100×0.1=10,
b=100-10-18-35-12=25,
n=25÷100=0.25.
故答案为:10,25,0.25;
(2)如图,即为补充完整的频数分布直方图;
(3)81≤x<91这一分数段所占的圆心角度数为360×0.35=126°;
故答案为:126;
(4)∵2500××=90(人)
∴估算全校获得二等奖的学生人数为90人.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
