人教版九年级上册数学22.3实际问题与二次函数课时练习(含答案)
文档属性
| 名称 | 人教版九年级上册数学22.3实际问题与二次函数课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 353.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 13:45:01 | ||
图片预览

文档简介
人教版九年级上册数学22.3实际问题与二次函数课时练习
一、单选题
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.一个球从地面坚直向上弹起时的速度为10米/秒,经过(秒)时球距离地面的高度(米)适用公式,那么球弹起后又回到地面所花的时间(秒)是( )
A.5 B.10 C.1 D.2
3.如图,将边长为4cm的正方形沿其对角线剪开,再把沿方向平移,得到,若两个三角形重叠部分的面积是,则它移动的距离等于( )
A.1cm B.2cm C.3cm D.1cm或3cm
4.如图,在菱形中,,,矩形的四个顶点分别在菱形的四边上,则矩形的最大面积为( )
A. B. C. D.
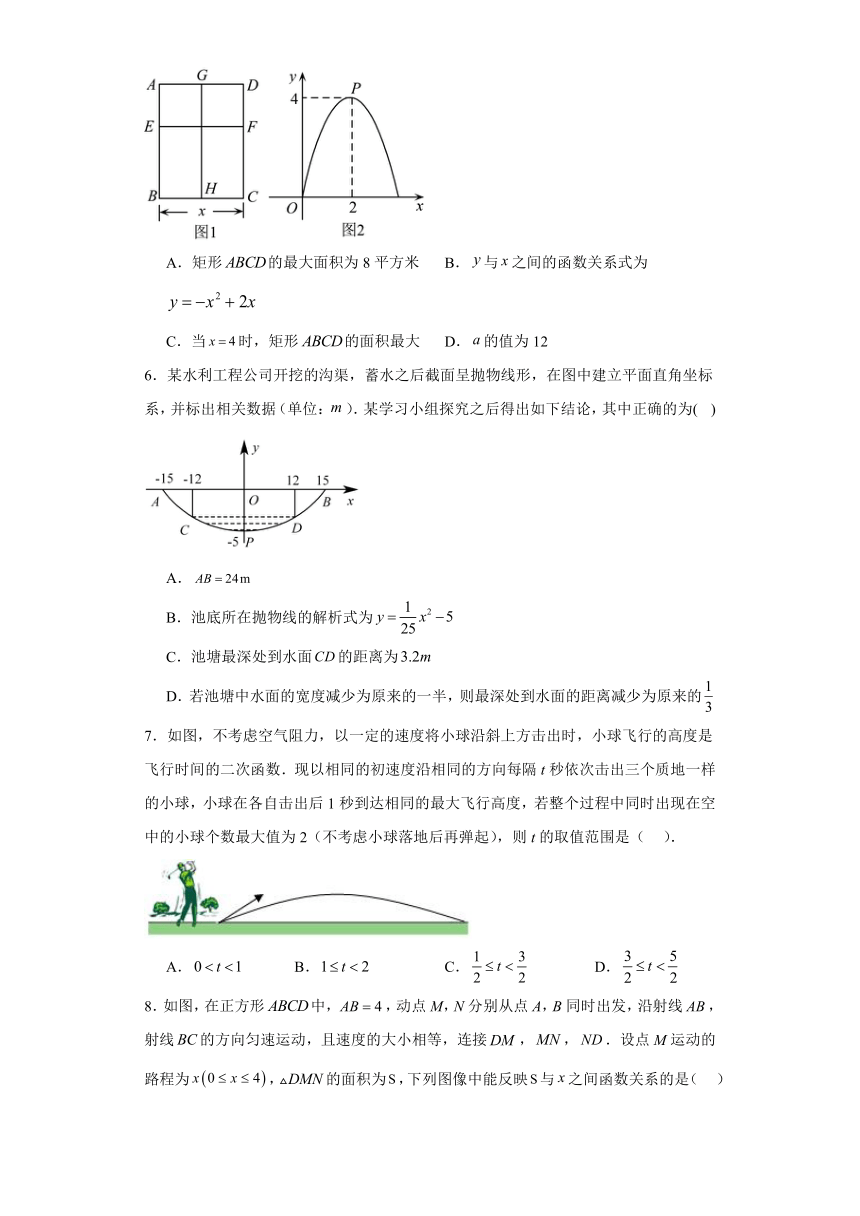
5.如图1所示的矩形窗框的周长及其两条隔断、的总长为米,且隔断、分别与矩形的两条邻边平行,设的长为米,矩形的面积为平方米,关于的函数图像如图2,则下列说法正确的是( )
A.矩形的最大面积为8平方米 B.与之间的函数关系式为
C.当时,矩形的面积最大 D.的值为12
6.某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:).某学习小组探究之后得出如下结论,其中正确的为( )
A.
B.池底所在抛物线的解析式为
C.池塘最深处到水面的距离为
D.若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
7.如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球飞行的高度是飞行时间的二次函数.现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球,小球在各自击出后1秒到达相同的最大飞行高度,若整个过程中同时出现在空中的小球个数最大值为2(不考虑小球落地后再弹起),则t的取值范围是( ).
A. B. C. D.
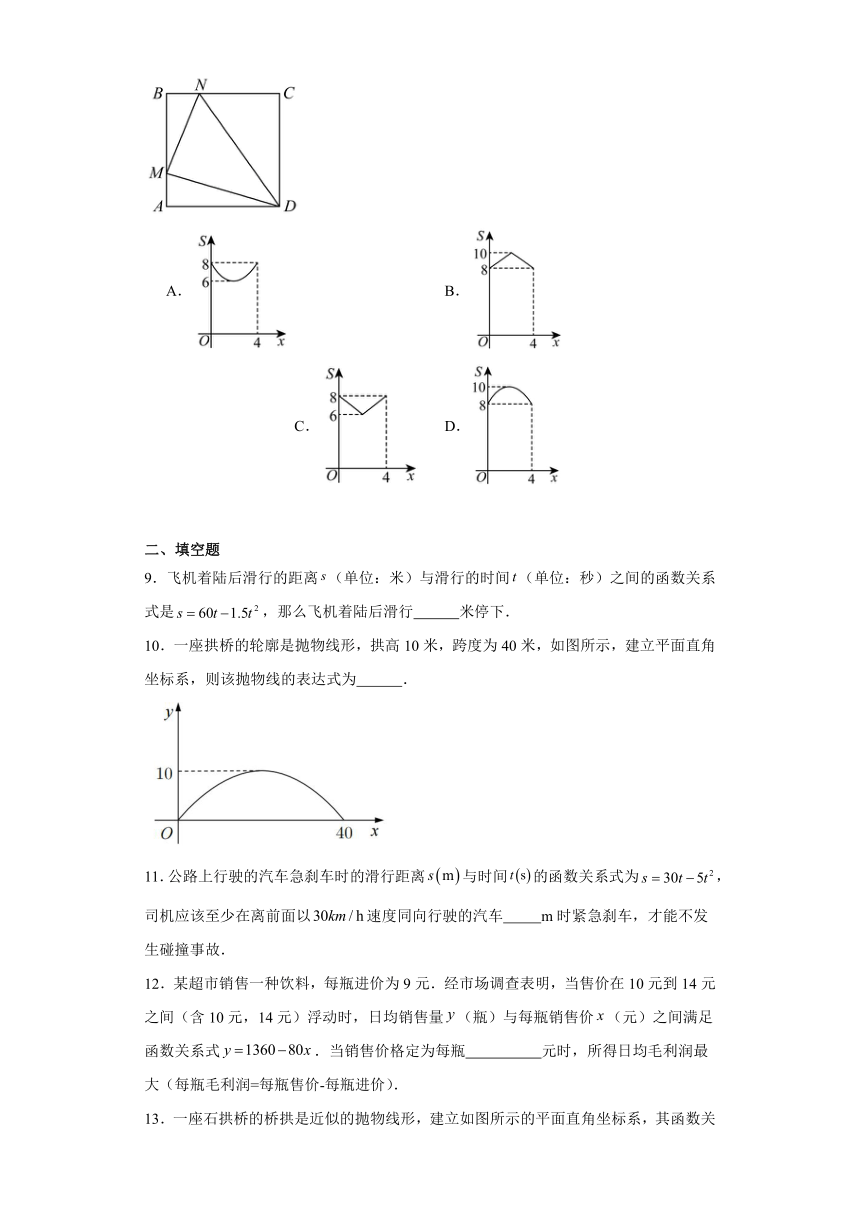
8.如图,在正方形中,,动点M,N分别从点A,B同时出发,沿射线,射线的方向匀速运动,且速度的大小相等,连接,,.设点M运动的路程为,的面积为,下列图像中能反映与之间函数关系的是( )
A. B. C. D.
二、填空题
9.飞机着陆后滑行的距离(单位:米)与滑行的时间(单位:秒)之间的函数关系式是,那么飞机着陆后滑行 米停下.
10.一座拱桥的轮廓是抛物线形,拱高10米,跨度为40米,如图所示,建立平面直角坐标系,则该抛物线的表达式为 .
11.公路上行驶的汽车急刹车时的滑行距离与时间的函数关系式为,司机应该至少在离前面以速度同向行驶的汽车 m时紧急刹车,才能不发生碰撞事故.
12.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数关系式.当销售价格定为每瓶 元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).
13.一座石拱桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数关系为,当水面的宽度为16米时,水面离桥拱顶的高度为 m.
14.体育老师将小华实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为,由此可知小华此次实心球训练的成绩为 米.
15.用总长为a米的铝合金材料做成如图1所示的“日”字形窗框(材料厚度忽略不计),窗户的透光面积y(米2)与窗框的宽x(米)之间的函数图象如图2所示,则a的值是 .
16.某初三学生对自己某次实心球训练时不慎脱手,发现实心球飞行高度(米)与水平距离(米)之间的关系为,由此可知该考生此次实心球训练的成绩为 米.
三、解答题
17.某商店购进一批单价为元的日用商品,如果以单价元销售,那么每月可售出件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高元,销售量相应减少件.销售单价为多少元时,每月获得的利润最大?最大利润是多少?
18.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,经市场调查发现,该产品每天的销量y(单位:千克)与售价x(单位:元/千克)有如下关系:.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)该产品售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的售价不高于每千克28元,该农户想要每天获得150元的销售利润,售价应定为每千克多少元?
19.商场某种商品销售成本为元/千克,若按元/千克,一个月可销售.经调查发现,每件商品每涨价元,月销售量就减少.设每件商品售价元、每月销售利润元,据此规律,请回答:
(1)求出与之间的函数关系式.
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
20.一位运动员投掷铅球的成绩是,当铅球运行的水平距离是时达到最大高度,若铅球运行的路线是抛物线,如图建立平面直角坐标系,
(1)求此抛物线的解析式;
(2)求铅球出手时距地面的高度.
参考答案:
1.C
2.D
3.D
4.D
5.D
6.C
7.B
8.A
9.600
10.
11.20
12.13
13.4
14.10
15.6
16.2
17.销售单价为元时,每月获得的销售利润最大,最大利润为元
18.(1)
(2)该产品售价定为每千克30元时,每天的销售利润最大,最大利润是200元;
(3)25
19.(1)与之间的函数关系式
(2)每件商品的售价定为元时,每个月可获得最大利润,最大的月利润是元
20.(1)
(2)
答案第1页,共2页
一、单选题
1.向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为、若此炮弹在第8秒与第16秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第10秒 C.第12秒 D.第15秒
2.一个球从地面坚直向上弹起时的速度为10米/秒,经过(秒)时球距离地面的高度(米)适用公式,那么球弹起后又回到地面所花的时间(秒)是( )
A.5 B.10 C.1 D.2
3.如图,将边长为4cm的正方形沿其对角线剪开,再把沿方向平移,得到,若两个三角形重叠部分的面积是,则它移动的距离等于( )
A.1cm B.2cm C.3cm D.1cm或3cm
4.如图,在菱形中,,,矩形的四个顶点分别在菱形的四边上,则矩形的最大面积为( )
A. B. C. D.
5.如图1所示的矩形窗框的周长及其两条隔断、的总长为米,且隔断、分别与矩形的两条邻边平行,设的长为米,矩形的面积为平方米,关于的函数图像如图2,则下列说法正确的是( )
A.矩形的最大面积为8平方米 B.与之间的函数关系式为
C.当时,矩形的面积最大 D.的值为12
6.某水利工程公司开挖的沟渠,蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:).某学习小组探究之后得出如下结论,其中正确的为( )
A.
B.池底所在抛物线的解析式为
C.池塘最深处到水面的距离为
D.若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的
7.如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球飞行的高度是飞行时间的二次函数.现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球,小球在各自击出后1秒到达相同的最大飞行高度,若整个过程中同时出现在空中的小球个数最大值为2(不考虑小球落地后再弹起),则t的取值范围是( ).
A. B. C. D.
8.如图,在正方形中,,动点M,N分别从点A,B同时出发,沿射线,射线的方向匀速运动,且速度的大小相等,连接,,.设点M运动的路程为,的面积为,下列图像中能反映与之间函数关系的是( )
A. B. C. D.
二、填空题
9.飞机着陆后滑行的距离(单位:米)与滑行的时间(单位:秒)之间的函数关系式是,那么飞机着陆后滑行 米停下.
10.一座拱桥的轮廓是抛物线形,拱高10米,跨度为40米,如图所示,建立平面直角坐标系,则该抛物线的表达式为 .
11.公路上行驶的汽车急刹车时的滑行距离与时间的函数关系式为,司机应该至少在离前面以速度同向行驶的汽车 m时紧急刹车,才能不发生碰撞事故.
12.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,日均销售量(瓶)与每瓶销售价(元)之间满足函数关系式.当销售价格定为每瓶 元时,所得日均毛利润最大(每瓶毛利润=每瓶售价-每瓶进价).
13.一座石拱桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数关系为,当水面的宽度为16米时,水面离桥拱顶的高度为 m.
14.体育老师将小华实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为,由此可知小华此次实心球训练的成绩为 米.
15.用总长为a米的铝合金材料做成如图1所示的“日”字形窗框(材料厚度忽略不计),窗户的透光面积y(米2)与窗框的宽x(米)之间的函数图象如图2所示,则a的值是 .
16.某初三学生对自己某次实心球训练时不慎脱手,发现实心球飞行高度(米)与水平距离(米)之间的关系为,由此可知该考生此次实心球训练的成绩为 米.
三、解答题
17.某商店购进一批单价为元的日用商品,如果以单价元销售,那么每月可售出件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高元,销售量相应减少件.销售单价为多少元时,每月获得的利润最大?最大利润是多少?
18.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,经市场调查发现,该产品每天的销量y(单位:千克)与售价x(单位:元/千克)有如下关系:.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)该产品售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的售价不高于每千克28元,该农户想要每天获得150元的销售利润,售价应定为每千克多少元?
19.商场某种商品销售成本为元/千克,若按元/千克,一个月可销售.经调查发现,每件商品每涨价元,月销售量就减少.设每件商品售价元、每月销售利润元,据此规律,请回答:
(1)求出与之间的函数关系式.
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
20.一位运动员投掷铅球的成绩是,当铅球运行的水平距离是时达到最大高度,若铅球运行的路线是抛物线,如图建立平面直角坐标系,
(1)求此抛物线的解析式;
(2)求铅球出手时距地面的高度.
参考答案:
1.C
2.D
3.D
4.D
5.D
6.C
7.B
8.A
9.600
10.
11.20
12.13
13.4
14.10
15.6
16.2
17.销售单价为元时,每月获得的销售利润最大,最大利润为元
18.(1)
(2)该产品售价定为每千克30元时,每天的销售利润最大,最大利润是200元;
(3)25
19.(1)与之间的函数关系式
(2)每件商品的售价定为元时,每个月可获得最大利润,最大的月利润是元
20.(1)
(2)
答案第1页,共2页
同课章节目录
