一元一次方程的应用(1)[上学期]
文档属性
| 名称 | 一元一次方程的应用(1)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-31 00:00:00 | ||
图片预览






文档简介
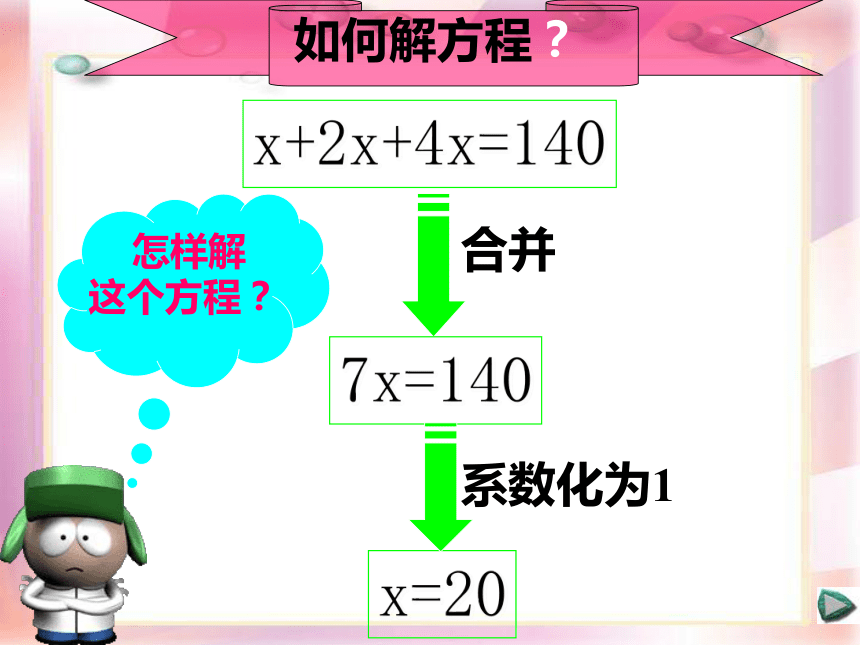
课件19张PPT。从古老的代数书说起—— 一元一次方程的讨论(1)海十中 杨永铭《对消与还原》 阿尔·花拉米子(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。 某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍。前年这个学校购买了多少台计算机? 设前年购买计算机x台,可以表示出:去年购买计算机____台,今年购买计算机____台。问题中的相等关系是什么?如何列方程?2x4x例题欣赏前年购买量+去年购买量+今年购买量=140台x+2x+4x=140列一元一次方程解应用题的步骤:1、审题:弄清题意和数量关系;5、写出答案(包括单位名称)。4、解方程;3、由等量关系列出方程;2、设未知数,找等量关系;x+2x+4x=140合并7x=140x=20系数化为1 怎样解这个方程?猜一猜并解释你的结论x+2x+4x=?乘法对加法的分配律:a(b+c+d)=ab+ac+adab+ac+ad=a(b+c+d)x+2x+4x=?x+2x+4x=( 1+2+4 )x=9x(1)x+2x+4x(2)5y-3y-4y(3)4z-1.5z-2.5z=(1+2+4)x=7x=(5-3-4)y=-2y=(4-1.5-2.5)z合
并小试身手: =0解下列方程(1)5x-2x=9(3)-3x+0.5x=10(4)16y-2.5y-7.5y=10 喷灌和滴灌是比漫灌节水的灌溉方式。随着农业技术的现代化,节水灌溉得到逐步推广,灌溉三块同样大的试验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的25%和15%,三块地共用水420吨。每块地各用水多少吨?古诗趣题巍巍古寺在山林,不知寺内几多僧。三百六十四支碗,看看用尽不差争。三人共食一碗饭,四人共吃一碗羹。算来寺内几多僧。请问先生明算者,解:设寺内有和尚x 人,根据题意,得考考你饭碗数+汤碗数=364 丢番图(Diphantus)的墓志铭:过路人,这儿埋葬着丢番图请计算以下数目,便知他一生经过了多少寒暑他一生的六分之一是幸福的童年十二分之一是无忧的少年再过七分之一的生命旅程,他建立了幸福的家庭五年后儿子出生可怜的孩子只活了父亲岁数的一半就死了过了四年,老人在悲痛中死去请你算一算,丢番图一共活了多少年?请你算一算,丢番图一共活了多少年?丢番图(Diphantus)的墓志铭:过路人,这儿埋葬着丢番图请计算以下数目,便知他一生经过了多少寒暑他一生的六分之一是幸福的童年十二分之一是无忧的少年再过七分之一的生命旅程,他建立了幸福的家庭五年后儿子出生可怜的孩子只活了父亲岁数的一半就死了过了四年,老人在悲痛中死去移项《对消与还原》 阿尔·花拉米子(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。 指的就是“合并”与“移项” 这节课我们对一元一次方程进行了讨论,你有何新的收获和体会?你来总结七嘴八舌说一说小结1、“合并”是一种恒等变性,它使方程变得简单,更接近x=a的形式。
2、“总量=所有分量之和”是本节课列方程解应用题所依据的相等关系。配制一种农药,其中生石灰,硫磺粉和水的重量比为1:3:12,要配置这种农药2272克,各种原料各需多少千克?解:设生石灰需x千克,硫磺需3x千克,水需12x千克,根据题意得:x+3x+12x=2272合并,得:16x=2272系数化为1,得:x=142,则3x=426,12x=1704答:要配置农药2272千克,生石灰需142千克,硫磺需426千克,水需1704千克。 推荐作业课本118页第1、3大题
(作业本) 谢谢各位,
再见!
并小试身手: =0解下列方程(1)5x-2x=9(3)-3x+0.5x=10(4)16y-2.5y-7.5y=10 喷灌和滴灌是比漫灌节水的灌溉方式。随着农业技术的现代化,节水灌溉得到逐步推广,灌溉三块同样大的试验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式,后两种方式用水量分别是漫灌的25%和15%,三块地共用水420吨。每块地各用水多少吨?古诗趣题巍巍古寺在山林,不知寺内几多僧。三百六十四支碗,看看用尽不差争。三人共食一碗饭,四人共吃一碗羹。算来寺内几多僧。请问先生明算者,解:设寺内有和尚x 人,根据题意,得考考你饭碗数+汤碗数=364 丢番图(Diphantus)的墓志铭:过路人,这儿埋葬着丢番图请计算以下数目,便知他一生经过了多少寒暑他一生的六分之一是幸福的童年十二分之一是无忧的少年再过七分之一的生命旅程,他建立了幸福的家庭五年后儿子出生可怜的孩子只活了父亲岁数的一半就死了过了四年,老人在悲痛中死去请你算一算,丢番图一共活了多少年?请你算一算,丢番图一共活了多少年?丢番图(Diphantus)的墓志铭:过路人,这儿埋葬着丢番图请计算以下数目,便知他一生经过了多少寒暑他一生的六分之一是幸福的童年十二分之一是无忧的少年再过七分之一的生命旅程,他建立了幸福的家庭五年后儿子出生可怜的孩子只活了父亲岁数的一半就死了过了四年,老人在悲痛中死去移项《对消与还原》 阿尔·花拉米子(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。 指的就是“合并”与“移项” 这节课我们对一元一次方程进行了讨论,你有何新的收获和体会?你来总结七嘴八舌说一说小结1、“合并”是一种恒等变性,它使方程变得简单,更接近x=a的形式。
2、“总量=所有分量之和”是本节课列方程解应用题所依据的相等关系。配制一种农药,其中生石灰,硫磺粉和水的重量比为1:3:12,要配置这种农药2272克,各种原料各需多少千克?解:设生石灰需x千克,硫磺需3x千克,水需12x千克,根据题意得:x+3x+12x=2272合并,得:16x=2272系数化为1,得:x=142,则3x=426,12x=1704答:要配置农药2272千克,生石灰需142千克,硫磺需426千克,水需1704千克。 推荐作业课本118页第1、3大题
(作业本) 谢谢各位,
再见!
