北师版高中数学必修第一册2.4二次函数性质的再研究 课件(共30张PPT)
文档属性
| 名称 | 北师版高中数学必修第一册2.4二次函数性质的再研究 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 14:31:18 | ||
图片预览











文档简介
(共30张PPT)
第二章 函 数
§4 二次函数性质的再研究
1.能熟练地对一般的二次函数的解析式进行配方,理解在二次函数的图像中a,b,c(或a,h,k)的作用;
2.研究二次函数图像移动的方法,并能迁移到其他函数;
3.掌握二次函数的三种不同表示形式,能正确地运用题设条件求出解析式,并能将函数解析式和图像进行正确转换;
4.掌握二次函数的性质:定义域、值域、单调性及最值;
5.掌握二次函数在闭区间上的最值的求法,初步学会求含有参数的二次函数的值域和最值.
问题导学
题型探究
达标检测
学习目标
知识点一 二次函数的配方法
思考 y=4x2-4x-1如何配方?你能由此求出方程4x2-4x-1=0的根吗?
答案
问题导学 新知探究 点点落实
令y=0,即4x2-4x-1=0,
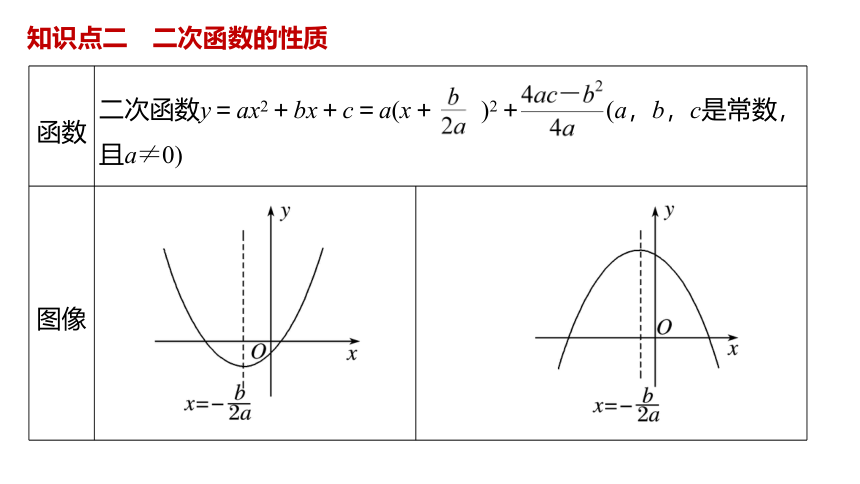
知识点二 二次函数的性质
函数 二次函数y=ax2+bx+c=a(x+ )2+ (a,b,c是常数,且a≠0) 图像
性 质 开口 向上 向下
对称轴 方程
顶点 坐标
单调性 在区间(-∞, ]上是减函数, 在区间[ ,+∞)上是增函数 在区间(-∞, ]上是增函数,
在区间[ ,+∞)上是减函数
最值 当x= 时,y有最小值, ymin= 当x= 时,y有最大值,
ymax=
知识点三 图像变换
思考 y=x2和y=2(x+1)2+3的图像之间有什么关系?
答案 y=x2的图像各点纵坐标变为原来的2倍,可得y=2x2的图像;
再把y=2x2的图像向左平移1个单位,再上移3个单位,
得y=2(x+1)2+3的图像.
答案
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 二次函数的图像
例1 如图是二次函数y=ax2+bx+c图像的一部分,图像过点A(-3,0),对称轴为x=-1.给出下面四个结论:
①b2>4ac;②2a-b=1;③a-b+c=0;④5a其中正确的是( )
A.②④ B.①④
C.②③ D.①③
解析 因为图像开口向下且顶点纵坐标大于0,
所以b2-4ac>0,①正确;
结合图像,当x=-1时,y>0,即a-b+c>0,③错误;
由对称轴为x=-1知,b=2a,
因为5>2,a<0,所以5a<2a,即5a答案 B
反思与感悟
反思与感悟
处理二次函数y=ax2+bx+c(a≠0)的图像问题,主要是考虑其图像特征如开口、顶点、与x轴、y轴交点、对称轴等与系数a,b,c之间的关系.
解析答案
跟踪训练1 二次函数f(x)=x2+bx+c的图像向左平移2个单位长度,再向上平移3个单位长度,得到二次函数f(x)=x2-2x+1的图像,则b=______,c=______.
解析 f(x)=x2-2x+1=(x-1)2,其图像顶点为(1,0).
将二次函数f(x)=x2-2x+1的图像向下平移3个单位长度,
再向右平移2个单位长度后的图像的顶点为(3,-3),
得到的抛物线为y=(x-3)2-3,
即f(x)=x2+bx+c,
∴(x-3)2-3=x2+bx+c,即x2-6x+6=x2+bx+c,
∴b=-6,c=6.
-6
6
解析答案
类型二 二次函数解析式的求解
例2 已知二次函数y=ax2+bx+c(a≠0)的图像与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.
反思与感悟
解 方法一 因为二次函数图像的对称轴是x=-1,
又顶点M到x轴的距离为2,
所以顶点的坐标为(-1,2)或(-1,-2),
故可得二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.
因为图像过点A(-3,0),
所以0=a(-3+1)2+2或0=a(-3+1)2-2,
解析答案
反思与感悟
方法二 因为二次函数图像的对称轴为x=-1,
又图像过点A(-3,0),
所以点A关于对称轴的对称点A′(1,0)也在图像上,
所以可得二次函数的解析式为y=a(x+3)(x-1).
由题意得顶点坐标为(-1,2)或(-1,-2),
反思与感悟
反思与感悟
求二次函数解析式的常见设法
(1)一般式,设为y=ax2+bx+c(a≠0);
(2)顶点式,若已知二次函数图像的顶点为(h,k),则函数的解析式可以设为y=a(x-h)2+k(a≠0);
(3)两根式,若已知二次函数y=ax2+bx+c(a≠0)对应的方程ax2+bx+c=0(a≠0)有两个根x1,x2,则函数的解析式可以设为y=a(x-x1)(x-x2)(a≠0).
利用已知条件寻找对应的设法,往往可使函数解析式的求解变得简单.
解析答案
跟踪训练2 已知f(x)是关于x的二次函数,且满足f(0)=1,f(x+1)=f(x)+2x,求f(x)的解析式.
解 设二次函数的解析式为f(x)=ax2+bx+c(a≠0),
故二次函数的解析式为f(x)=x2-x+1.
解析答案
类型三 二次函数的最值或值域
(1)求函数图像的顶点坐标、对称轴方程和最值;
解析答案
(2)若x∈[1,4],求函数值域.
解 由于3∈[1,4],所以函数在区间[1,3]上是减函数,
反思与感悟
反思与感悟
跟踪训练3 已知函数f(x)=ax2+2ax+1在区间[-1,2]上有最大值4,
求实数a的值.
解 f(x)=a(x+1)2+1-a.
(1)当a=0时,函数f(x)在区间[-1,2]上的值不变,
恒为常数1,不符合题意,舍去.
(2)当a>0时,函数f(x)在区间[-1,2]上是增函数,
(3)当a<0时,函数f(x)在区间[-1,2]上是减函数,
最大值为f(-1)=1-a=4,解得a=-3.
解析答案
返回
1
2
3
解析答案
达标检测
4
1.二次函数f(x)=ax2+bx+c(a≠0)与g(x)=bx2+ax+c(b≠0)的图像可能是下图中的( )
5
1
2
3
4
5
即f(x),g(x)的图像的对称轴位于y轴的同一侧,由此排除A,B;
由C,D中给出的图像,可判定f(x),g(x)的图像的开口方向相反,
即f(x),g(x)的图像的对称轴都位于y轴右侧,排除C,选D.
答案 D
解析答案
2.设二次函数y=f(x)满足f(4+x)=f(4-x),又f(x)在[4,+∞)上是减函数,且f(a)≥f(0),则实数a的取值范围是( )
A.a≥4 B.0≤a≤8
C.a<0 D.a<0或a≥8
解析 由题意知二次函数f(x)的图像关于直线x=4对称,
则有f(0)=f(8).因为f(x)在[4,+∞)上是减函数,
所以在(-∞,4]上是增函数.
当a∈(-∞,4]时,由f(a)≥f(0),得0≤a≤4;
当a∈[4,+∞)时,由f(a)≥f(0),即f(a)≥f(8),得4≤a≤8.
综上可知0≤a≤8.
1
2
3
4
5
B
解析答案
3.已知f(x)=x2+bx+c,且f(-1)=f(3),则( )
A.f(1)>c>f(-1) B.f(1)C.c>f(-1)>f(1) D.c解析 因为f(-1)=f(3),
所以f(x)图像的对称轴为x=1,
因此函数在区间(-∞,1]上是减函数,
又c=f(0),所以f(1)1
2
3
4
5
B
解析答案
4.已知二次函数f(x)=x2-6x+8,x∈[2,a]且f(x)的最小值为f(a),
则a的取值范围是_____.
解析 二次函数f(x)的图像的对称轴为x=3,
要使f(x)=x2-6x+8在区间[2,a]上的最小值为f(a),
只需函数f(x)在区间[2,a]上是减函数,
所以21
2
3
4
5
(2,3]
解析答案
5.已知二次函数y= x2+2x+1.
(1)写出函数图像的开口方向、顶点坐标、对称轴、最值,并指出它可由y=x2的图像怎样变化得到;
∴函数图像的开口向上,顶点坐标是(-2,-1),对称轴是直线x=-2.
1
2
3
4
5
解析答案
(2)求函数图像与y轴、x轴的交点;
解 令x=0,则y=1,
1
2
3
4
5
∴函数图像与y轴交于(0,1).
(3)作出函数的图像;
解 函数图像如图.
解析答案
(4)求函数的单调区间;
解 由图像可知,函数的单调递减区间是(-∞,-2],
单调递增区间是[-2,+∞).
(5)观察图像:当x为何值时,y>0?当x为何值时,y=0?当x为何值时,y<0
1
2
3
4
5
返回
规律与方法
1.配方法是重要的数学方法,在处理二次函数图像变换,
研究二次函数性质时使用频繁.
2.二次函数图像变换规律可以推广到一般函数,即:
本课结束
第二章 函 数
§4 二次函数性质的再研究
1.能熟练地对一般的二次函数的解析式进行配方,理解在二次函数的图像中a,b,c(或a,h,k)的作用;
2.研究二次函数图像移动的方法,并能迁移到其他函数;
3.掌握二次函数的三种不同表示形式,能正确地运用题设条件求出解析式,并能将函数解析式和图像进行正确转换;
4.掌握二次函数的性质:定义域、值域、单调性及最值;
5.掌握二次函数在闭区间上的最值的求法,初步学会求含有参数的二次函数的值域和最值.
问题导学
题型探究
达标检测
学习目标
知识点一 二次函数的配方法
思考 y=4x2-4x-1如何配方?你能由此求出方程4x2-4x-1=0的根吗?
答案
问题导学 新知探究 点点落实
令y=0,即4x2-4x-1=0,
知识点二 二次函数的性质
函数 二次函数y=ax2+bx+c=a(x+ )2+ (a,b,c是常数,且a≠0) 图像
性 质 开口 向上 向下
对称轴 方程
顶点 坐标
单调性 在区间(-∞, ]上是减函数, 在区间[ ,+∞)上是增函数 在区间(-∞, ]上是增函数,
在区间[ ,+∞)上是减函数
最值 当x= 时,y有最小值, ymin= 当x= 时,y有最大值,
ymax=
知识点三 图像变换
思考 y=x2和y=2(x+1)2+3的图像之间有什么关系?
答案 y=x2的图像各点纵坐标变为原来的2倍,可得y=2x2的图像;
再把y=2x2的图像向左平移1个单位,再上移3个单位,
得y=2(x+1)2+3的图像.
答案
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 二次函数的图像
例1 如图是二次函数y=ax2+bx+c图像的一部分,图像过点A(-3,0),对称轴为x=-1.给出下面四个结论:
①b2>4ac;②2a-b=1;③a-b+c=0;④5a
A.②④ B.①④
C.②③ D.①③
解析 因为图像开口向下且顶点纵坐标大于0,
所以b2-4ac>0,①正确;
结合图像,当x=-1时,y>0,即a-b+c>0,③错误;
由对称轴为x=-1知,b=2a,
因为5>2,a<0,所以5a<2a,即5a
反思与感悟
反思与感悟
处理二次函数y=ax2+bx+c(a≠0)的图像问题,主要是考虑其图像特征如开口、顶点、与x轴、y轴交点、对称轴等与系数a,b,c之间的关系.
解析答案
跟踪训练1 二次函数f(x)=x2+bx+c的图像向左平移2个单位长度,再向上平移3个单位长度,得到二次函数f(x)=x2-2x+1的图像,则b=______,c=______.
解析 f(x)=x2-2x+1=(x-1)2,其图像顶点为(1,0).
将二次函数f(x)=x2-2x+1的图像向下平移3个单位长度,
再向右平移2个单位长度后的图像的顶点为(3,-3),
得到的抛物线为y=(x-3)2-3,
即f(x)=x2+bx+c,
∴(x-3)2-3=x2+bx+c,即x2-6x+6=x2+bx+c,
∴b=-6,c=6.
-6
6
解析答案
类型二 二次函数解析式的求解
例2 已知二次函数y=ax2+bx+c(a≠0)的图像与x轴相交于点A(-3,0),对称轴为x=-1,顶点M到x轴的距离为2,求此函数的解析式.
反思与感悟
解 方法一 因为二次函数图像的对称轴是x=-1,
又顶点M到x轴的距离为2,
所以顶点的坐标为(-1,2)或(-1,-2),
故可得二次函数的解析式为y=a(x+1)2+2或y=a(x+1)2-2.
因为图像过点A(-3,0),
所以0=a(-3+1)2+2或0=a(-3+1)2-2,
解析答案
反思与感悟
方法二 因为二次函数图像的对称轴为x=-1,
又图像过点A(-3,0),
所以点A关于对称轴的对称点A′(1,0)也在图像上,
所以可得二次函数的解析式为y=a(x+3)(x-1).
由题意得顶点坐标为(-1,2)或(-1,-2),
反思与感悟
反思与感悟
求二次函数解析式的常见设法
(1)一般式,设为y=ax2+bx+c(a≠0);
(2)顶点式,若已知二次函数图像的顶点为(h,k),则函数的解析式可以设为y=a(x-h)2+k(a≠0);
(3)两根式,若已知二次函数y=ax2+bx+c(a≠0)对应的方程ax2+bx+c=0(a≠0)有两个根x1,x2,则函数的解析式可以设为y=a(x-x1)(x-x2)(a≠0).
利用已知条件寻找对应的设法,往往可使函数解析式的求解变得简单.
解析答案
跟踪训练2 已知f(x)是关于x的二次函数,且满足f(0)=1,f(x+1)=f(x)+2x,求f(x)的解析式.
解 设二次函数的解析式为f(x)=ax2+bx+c(a≠0),
故二次函数的解析式为f(x)=x2-x+1.
解析答案
类型三 二次函数的最值或值域
(1)求函数图像的顶点坐标、对称轴方程和最值;
解析答案
(2)若x∈[1,4],求函数值域.
解 由于3∈[1,4],所以函数在区间[1,3]上是减函数,
反思与感悟
反思与感悟
跟踪训练3 已知函数f(x)=ax2+2ax+1在区间[-1,2]上有最大值4,
求实数a的值.
解 f(x)=a(x+1)2+1-a.
(1)当a=0时,函数f(x)在区间[-1,2]上的值不变,
恒为常数1,不符合题意,舍去.
(2)当a>0时,函数f(x)在区间[-1,2]上是增函数,
(3)当a<0时,函数f(x)在区间[-1,2]上是减函数,
最大值为f(-1)=1-a=4,解得a=-3.
解析答案
返回
1
2
3
解析答案
达标检测
4
1.二次函数f(x)=ax2+bx+c(a≠0)与g(x)=bx2+ax+c(b≠0)的图像可能是下图中的( )
5
1
2
3
4
5
即f(x),g(x)的图像的对称轴位于y轴的同一侧,由此排除A,B;
由C,D中给出的图像,可判定f(x),g(x)的图像的开口方向相反,
即f(x),g(x)的图像的对称轴都位于y轴右侧,排除C,选D.
答案 D
解析答案
2.设二次函数y=f(x)满足f(4+x)=f(4-x),又f(x)在[4,+∞)上是减函数,且f(a)≥f(0),则实数a的取值范围是( )
A.a≥4 B.0≤a≤8
C.a<0 D.a<0或a≥8
解析 由题意知二次函数f(x)的图像关于直线x=4对称,
则有f(0)=f(8).因为f(x)在[4,+∞)上是减函数,
所以在(-∞,4]上是增函数.
当a∈(-∞,4]时,由f(a)≥f(0),得0≤a≤4;
当a∈[4,+∞)时,由f(a)≥f(0),即f(a)≥f(8),得4≤a≤8.
综上可知0≤a≤8.
1
2
3
4
5
B
解析答案
3.已知f(x)=x2+bx+c,且f(-1)=f(3),则( )
A.f(1)>c>f(-1) B.f(1)
所以f(x)图像的对称轴为x=1,
因此函数在区间(-∞,1]上是减函数,
又c=f(0),所以f(1)
2
3
4
5
B
解析答案
4.已知二次函数f(x)=x2-6x+8,x∈[2,a]且f(x)的最小值为f(a),
则a的取值范围是_____.
解析 二次函数f(x)的图像的对称轴为x=3,
要使f(x)=x2-6x+8在区间[2,a]上的最小值为f(a),
只需函数f(x)在区间[2,a]上是减函数,
所以2
2
3
4
5
(2,3]
解析答案
5.已知二次函数y= x2+2x+1.
(1)写出函数图像的开口方向、顶点坐标、对称轴、最值,并指出它可由y=x2的图像怎样变化得到;
∴函数图像的开口向上,顶点坐标是(-2,-1),对称轴是直线x=-2.
1
2
3
4
5
解析答案
(2)求函数图像与y轴、x轴的交点;
解 令x=0,则y=1,
1
2
3
4
5
∴函数图像与y轴交于(0,1).
(3)作出函数的图像;
解 函数图像如图.
解析答案
(4)求函数的单调区间;
解 由图像可知,函数的单调递减区间是(-∞,-2],
单调递增区间是[-2,+∞).
(5)观察图像:当x为何值时,y>0?当x为何值时,y=0?当x为何值时,y<0
1
2
3
4
5
返回
规律与方法
1.配方法是重要的数学方法,在处理二次函数图像变换,
研究二次函数性质时使用频繁.
2.二次函数图像变换规律可以推广到一般函数,即:
本课结束
