人教版高中数学必修第一册第一章 集合 章末复习课课件(共24张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册第一章 集合 章末复习课课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 570.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 12:00:03 | ||
图片预览







文档简介
(共24张PPT)
第一章 集 合
章末复习课
1.系统和深化对集合基础知识的理解与掌握;
2.重点掌握好集合间的关系与集合的基本运算.
问题导学
题型探究
达标检测
学习目标
1.集合元素的三个特性:______,______,______.
2.元素与集合有且只有两种关系:___,___.
3.已经学过的集合表示方法有_______,_______,______,
_________________.
答案
问题导学 新知探究 点点落实
确定性
互异性
无序性
∈
列举法
描述法
Venn图
常用数集字母代号
答案
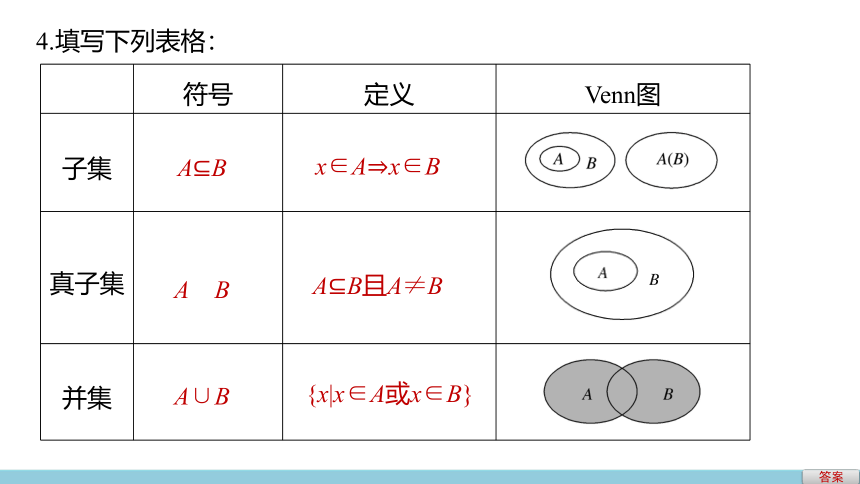
4.填写下列表格:
符号 定义 Venn图
子集
真子集
并集
A B
x∈A x∈B
A?B
A B且A≠B
A∪B
{x|x∈A或x∈B}
答案
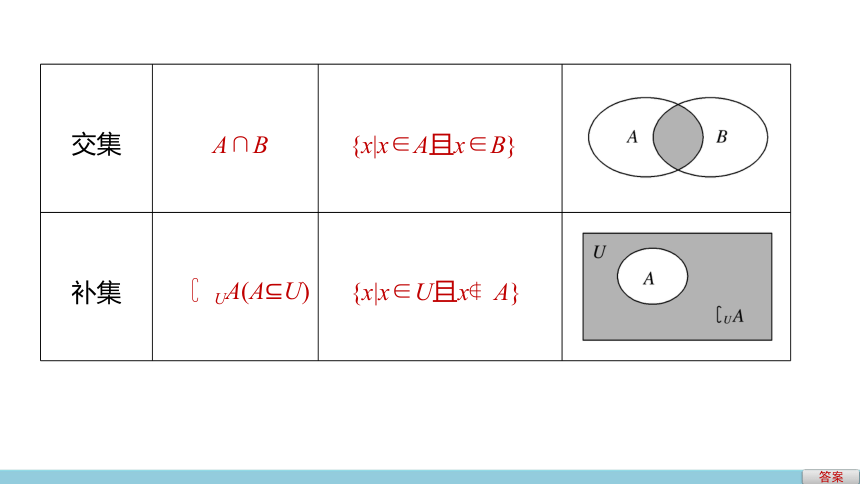
交集
补集
A∩B
{x|x∈A且x∈B}
UA(A U)
{x|x∈U且x A}
5.常用结论
(1) ___A;
(2)A∪ =____;A∪A=____;A∪B=A ____.
(3)A∩ =____;A∩A=____;A∩B=A _____.
(4)A∪( UA)=___;A∩( UA)=___; U( UA)=___.
A
A B
A
A
A B
U
A
答案
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 集合的概念
例1 设集合A={(x,y)|x-y=0},B={(x,y)|2x-3y+4=0},则A∩B=_______.
∴A∩B={(4,4)}.
{(4,4)}
反思与感悟 要解决集合的概念问题,必须先弄清集合中元素的性质,明确是数集,还是点集等.
解析答案
所以a=-1,b=1.所以b-a=2.
2
解析答案
类型二 集合间的基本关系
例2 若集合P={x|x2+x-6=0},S={x|ax+1=0},且S P,求由a的可能取值组成的集合.
解 由题意得,P={-3,2}.
当a=0时,S= ,满足S P;
反思与感悟
反思与感悟
1.在解决两个数集关系问题时,合理运用数轴分析与求解可避免出错.在解含有参数的不等式(或方程)时,要对参数进行分类讨论,分类时要遵循“不重不漏”的原则,然后对于每一类情况都要给出问题的解答.
2.对于两集合A,B,当A B时,不要忽略A= 的情况.
解析答案
跟踪训练2 设集合A={x|x2-3x+2=0},集合B={x|x2-4x+a=0,a为常数},若B A,求实数a的取值范围.
解 由已知得A={1,2}.若B A,则集合B有两种情况,B= 或B≠ .
当B= 时,方程x2-4x+a=0无实根,
当B≠ 时,若Δ=0,则有a=4,B={2} A满足条件;
若Δ>0,则1,2是方程x2-4x+a=0的根,
但由根与系数的关系知矛盾,故Δ>0不成立.
∴当B≠ 时,a=4.
综上所述,满足B A时,a的取值范围是a≥4.
∴满足B A的a的取值范围是a<4.
∴Δ=16-4a<0,∴a>4.
解析答案
类型三 集合的交、并、补运算
例3 设全集为R,A={x|3≤x<7},B={x|2解 把全集R和集合A、B在数轴上表示如下:
由图知,A∪B={x|2∴ R(A∪B)={x|x≤2或x≥10},
∴( RA)∩B={x|2∵ RA={x|x<3或x≥7}.
反思与感悟 求解用不等式表示的数集间的集合运算时,一般要借助于数轴求解,此法的特点是简单直观,同时要注意各个端点的画法及取到与否.
反思与感悟
解析答案
跟踪训练3 已知集合U={x|0≤x≤6,x∈Z},A={1,3,6},B={1,4,5},则A∩( UB)等于( )
A.{1} B.{3,6}
C.{4,5} D.{1,3,4,5,6}
解析 ∵U={0,1,2,3,4,5,6},B={1,4,5},
∴ UB={0,2,3,6},
又∵A={1,3,6},
∴A∩( UB)={3,6},选B.
B
解析答案
类型四 集合的实际应用
例4 向50名学生调查对A,B两事件的态度,有如下结果:赞成A的人数是全体的五分之三,其余的不赞成;赞成B的比赞成A的多3人,其余的不赞成;另外,对A,B都不赞成的学生数比对A,B都赞成的学生数的三分之一多1人.问对A,B都赞成的学生和都不赞成的学生各有多少人?
反思与感悟
赞成B的人数为30+3=33,记50名学生组成的集合为U;
赞成事件A的学生全体为集合M;赞成事件B的学生全体为集合N.
设对事件A,B都赞成的学生人数为x,
赞成A而不赞成B的人数为30-x,赞成B而不赞成A的人数为33-x.
则Venn图如图所示:
所以对A,B都赞成的学生有21人,都不赞成的学生有8人.
反思与感悟
反思与感悟
解决这一类问题一般用数形结合思想,借助于Venn图,把抽象的数学语言与直观的图形结合起来,注意两个集合并集的元素个数不一定等于两个集合的元素个数和.
跟踪训练4 学校举办了排球赛,某班45名同学中有12名同学参赛,后来又举办了田径赛,这个班有20名同学参赛,已知两项都参赛的有6名同学,两项比赛中,这个班共有多少名同学没有参加过比赛?
解 设A={x|x为参加排球赛的同学},B={x|x为参加田径赛的同学},
则A∩B={x|x为参加两项比赛的同学}.
画出Venn图(如图),
可知没有参加过比赛的同学有:
45-(12+20-6)=19(名).
答 这个班共有19名同学没有参加过比赛.
解析答案
返回
1
2
3
达标检测
4
1.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有( )
A.2个 B.4个
C.6个 D.8个
5
B
答案
2.已知2a∈A,a2-a∈A,若A只含这2个元素,则下列说法中正确的
是( )
A.a可取全体实数
B.a可取除去0以外的所有实数
C.a可取除去3以外的所有实数
D.a可取除去0和3以外的所有实数
1
2
3
4
5
D
答案
1
2
3
4
5
D
答案
4.设全集I={a,b,c,d,e},集合M={a,b,c},N={b,d,e},
那么( IM)∩( IN)等于( )
A. B.{d}
C.{b,e} D.{a,c}
1
2
3
4
5
A
答案
5.已知P={y|y=a2+1,a∈R},Q={m|m=x2-4x+5,x∈R},则P与Q的关系不正确的是( )
A.P Q B.P Q
C.P=Q D.P∩Q=
1
2
3
4
5
D
答案
返回
规律与方法
1.要注意区分两大关系:一是元素与集合的从属关系,二是集合与集合的包含关系.
2.在利用集合中元素相等列方程求未知数的值时,要注意利用集合中元素的互异性这一性质进行检验,忽视集合中元素的性质是导致错误的常见原因之一.
本课结束
第一章 集 合
章末复习课
1.系统和深化对集合基础知识的理解与掌握;
2.重点掌握好集合间的关系与集合的基本运算.
问题导学
题型探究
达标检测
学习目标
1.集合元素的三个特性:______,______,______.
2.元素与集合有且只有两种关系:___,___.
3.已经学过的集合表示方法有_______,_______,______,
_________________.
答案
问题导学 新知探究 点点落实
确定性
互异性
无序性
∈
列举法
描述法
Venn图
常用数集字母代号
答案
4.填写下列表格:
符号 定义 Venn图
子集
真子集
并集
A B
x∈A x∈B
A?B
A B且A≠B
A∪B
{x|x∈A或x∈B}
答案
交集
补集
A∩B
{x|x∈A且x∈B}
UA(A U)
{x|x∈U且x A}
5.常用结论
(1) ___A;
(2)A∪ =____;A∪A=____;A∪B=A ____.
(3)A∩ =____;A∩A=____;A∩B=A _____.
(4)A∪( UA)=___;A∩( UA)=___; U( UA)=___.
A
A B
A
A
A B
U
A
答案
返回
解析答案
反思与感悟
题型探究 重点难点 个个击破
类型一 集合的概念
例1 设集合A={(x,y)|x-y=0},B={(x,y)|2x-3y+4=0},则A∩B=_______.
∴A∩B={(4,4)}.
{(4,4)}
反思与感悟 要解决集合的概念问题,必须先弄清集合中元素的性质,明确是数集,还是点集等.
解析答案
所以a=-1,b=1.所以b-a=2.
2
解析答案
类型二 集合间的基本关系
例2 若集合P={x|x2+x-6=0},S={x|ax+1=0},且S P,求由a的可能取值组成的集合.
解 由题意得,P={-3,2}.
当a=0时,S= ,满足S P;
反思与感悟
反思与感悟
1.在解决两个数集关系问题时,合理运用数轴分析与求解可避免出错.在解含有参数的不等式(或方程)时,要对参数进行分类讨论,分类时要遵循“不重不漏”的原则,然后对于每一类情况都要给出问题的解答.
2.对于两集合A,B,当A B时,不要忽略A= 的情况.
解析答案
跟踪训练2 设集合A={x|x2-3x+2=0},集合B={x|x2-4x+a=0,a为常数},若B A,求实数a的取值范围.
解 由已知得A={1,2}.若B A,则集合B有两种情况,B= 或B≠ .
当B= 时,方程x2-4x+a=0无实根,
当B≠ 时,若Δ=0,则有a=4,B={2} A满足条件;
若Δ>0,则1,2是方程x2-4x+a=0的根,
但由根与系数的关系知矛盾,故Δ>0不成立.
∴当B≠ 时,a=4.
综上所述,满足B A时,a的取值范围是a≥4.
∴满足B A的a的取值范围是a<4.
∴Δ=16-4a<0,∴a>4.
解析答案
类型三 集合的交、并、补运算
例3 设全集为R,A={x|3≤x<7},B={x|2
由图知,A∪B={x|2
∴( RA)∩B={x|2
反思与感悟 求解用不等式表示的数集间的集合运算时,一般要借助于数轴求解,此法的特点是简单直观,同时要注意各个端点的画法及取到与否.
反思与感悟
解析答案
跟踪训练3 已知集合U={x|0≤x≤6,x∈Z},A={1,3,6},B={1,4,5},则A∩( UB)等于( )
A.{1} B.{3,6}
C.{4,5} D.{1,3,4,5,6}
解析 ∵U={0,1,2,3,4,5,6},B={1,4,5},
∴ UB={0,2,3,6},
又∵A={1,3,6},
∴A∩( UB)={3,6},选B.
B
解析答案
类型四 集合的实际应用
例4 向50名学生调查对A,B两事件的态度,有如下结果:赞成A的人数是全体的五分之三,其余的不赞成;赞成B的比赞成A的多3人,其余的不赞成;另外,对A,B都不赞成的学生数比对A,B都赞成的学生数的三分之一多1人.问对A,B都赞成的学生和都不赞成的学生各有多少人?
反思与感悟
赞成B的人数为30+3=33,记50名学生组成的集合为U;
赞成事件A的学生全体为集合M;赞成事件B的学生全体为集合N.
设对事件A,B都赞成的学生人数为x,
赞成A而不赞成B的人数为30-x,赞成B而不赞成A的人数为33-x.
则Venn图如图所示:
所以对A,B都赞成的学生有21人,都不赞成的学生有8人.
反思与感悟
反思与感悟
解决这一类问题一般用数形结合思想,借助于Venn图,把抽象的数学语言与直观的图形结合起来,注意两个集合并集的元素个数不一定等于两个集合的元素个数和.
跟踪训练4 学校举办了排球赛,某班45名同学中有12名同学参赛,后来又举办了田径赛,这个班有20名同学参赛,已知两项都参赛的有6名同学,两项比赛中,这个班共有多少名同学没有参加过比赛?
解 设A={x|x为参加排球赛的同学},B={x|x为参加田径赛的同学},
则A∩B={x|x为参加两项比赛的同学}.
画出Venn图(如图),
可知没有参加过比赛的同学有:
45-(12+20-6)=19(名).
答 这个班共有19名同学没有参加过比赛.
解析答案
返回
1
2
3
达标检测
4
1.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有( )
A.2个 B.4个
C.6个 D.8个
5
B
答案
2.已知2a∈A,a2-a∈A,若A只含这2个元素,则下列说法中正确的
是( )
A.a可取全体实数
B.a可取除去0以外的所有实数
C.a可取除去3以外的所有实数
D.a可取除去0和3以外的所有实数
1
2
3
4
5
D
答案
1
2
3
4
5
D
答案
4.设全集I={a,b,c,d,e},集合M={a,b,c},N={b,d,e},
那么( IM)∩( IN)等于( )
A. B.{d}
C.{b,e} D.{a,c}
1
2
3
4
5
A
答案
5.已知P={y|y=a2+1,a∈R},Q={m|m=x2-4x+5,x∈R},则P与Q的关系不正确的是( )
A.P Q B.P Q
C.P=Q D.P∩Q=
1
2
3
4
5
D
答案
返回
规律与方法
1.要注意区分两大关系:一是元素与集合的从属关系,二是集合与集合的包含关系.
2.在利用集合中元素相等列方程求未知数的值时,要注意利用集合中元素的互异性这一性质进行检验,忽视集合中元素的性质是导致错误的常见原因之一.
本课结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
