人教版七年级上册数学第二章整式的加减测试题一(含答案)
文档属性
| 名称 | 人教版七年级上册数学第二章整式的加减测试题一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 173.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 14:18:14 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版七年级上册数学第二章测试题一(附答案)
一、单选题(共12题;共24分)
1.下列选项中,与xy2是同类项的是( )
A. -2xy2 B. 2x2y C. xy D. x2y2
2.下列说法正确的是( )
A. 不是单项式 B. 单项式 的系数是1 C. ﹣7ad的次数是2 D. 3x﹣2y不是多项式
3.下列运算正确的是( )
A. 7x-(-3x)=10 B. 5a+6b=11ab C. ab+2ba=3ab D. -(a-b)=a+b
4.计算的结果是( )
A. 6 B. C. 2 D.
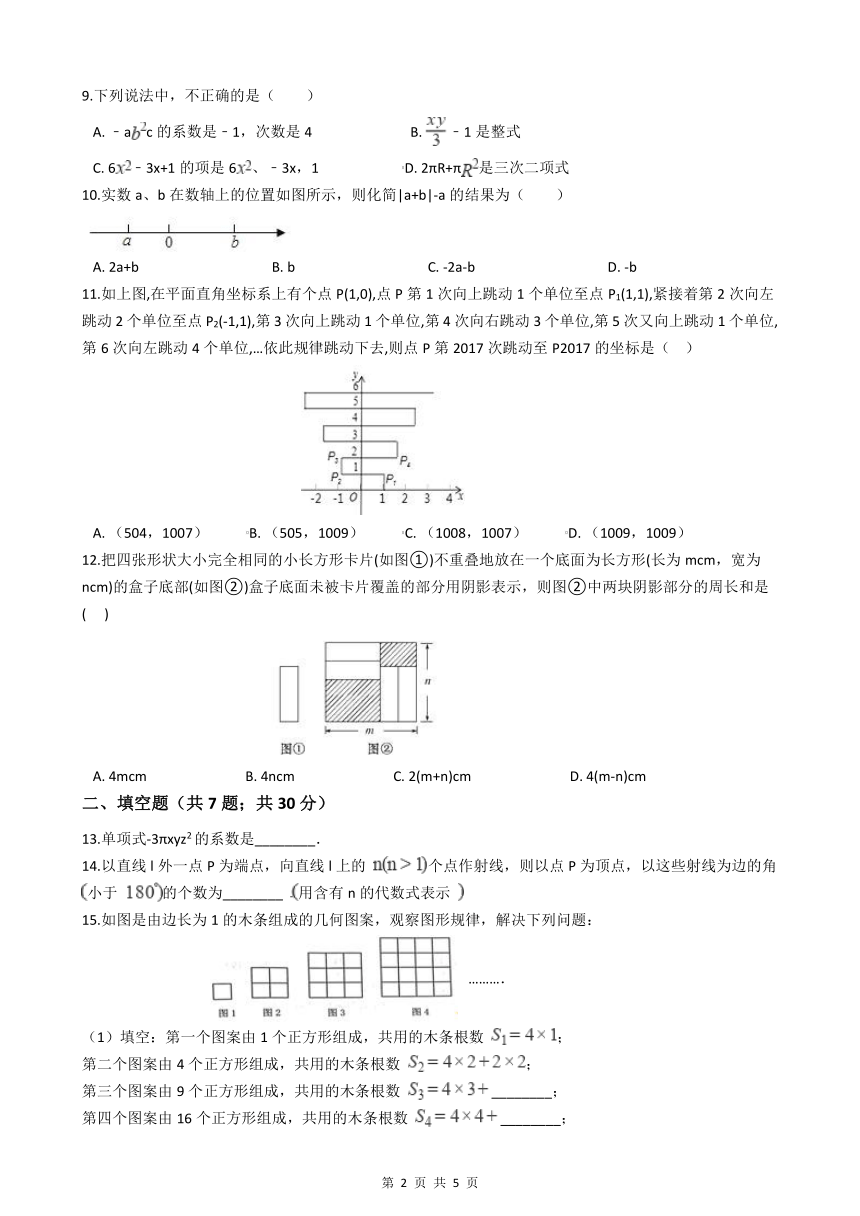
5.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A. (﹣1,0) B. (1,﹣2) C. (1,1) D. (﹣1,﹣1)
6.2010年广州亚运会吉祥物取名“乐羊羊”.图中各图是按照一定规律排列的羊的组图,图①有1只羊,图②有3只羊,……,则图⑩有( )只羊.
A. 53 B. 54 C. 55 D. 56
7.下列运算结果正确的是
A. B. C. D.
8.按一定规律排列的单项式:a,﹣a2 , a3 , ﹣a4 , a5 , ﹣a6 , ……,第n个单项式是( )
A. an B. ﹣an C. (﹣1)n+1an D. (﹣1)nan
9.下列说法中,不正确的是( )
A. ﹣ac的系数是﹣1,次数是4 B. ﹣1是整式
C. 6﹣3x+1的项是6、﹣3x,1 D. 2πR+π是三次二项式
10.实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )
A. 2a+b B. b C. -2a-b D. -b
11.如上图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
A. (504,1007) B. (505,1009) C. (1008,1007) D. (1009,1009)
12.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A. 4mcm B. 4ncm C. 2(m+n)cm D. 4(m-n)cm
二、填空题(共7题;共30分)
13.单项式-3πxyz2的系数是________.
14.以直线l外一点P为端点,向直线l上的 个点作射线,则以点P为顶点,以这些射线为边的角 小于 的个数为________ 用含有n的代数式表示
15.如图是由边长为1的木条组成的几何图案,观察图形规律,解决下列问题:
……….
(1)填空:第一个图案由1个正方形组成,共用的木条根数 ;
第二个图案由4个正方形组成,共用的木条根数 ;
第三个图案由9个正方形组成,共用的木条根数 ________;
第四个图案由16个正方形组成,共用的木条根数 ________;
(2)第 个图案由 个正方形组成,共用木条根数 ________(用含 的代数式表示)
16.如图,在平面直角坐标系中,已知点A(-4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(2)个三角形的直角顶点的坐标是________,第(2018)个三角形的直角顶点的坐标是________.
17.如图.乐乐班级举行“新春美食会”,同学们如图摆放桌椅,图(1)表示1张餐桌和6把椅子(三角形表示餐桌,每个小圆表示一把椅子),图(2)表示2张餐桌和8把椅子,图(3)表示3张餐桌和10把椅子,……;按照这种方式摆放12张餐桌,需要________把椅子.
18.如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1 , 第2次从点A1向右移动6个单位长度至点A2 , 第3次从点A2向左移动9个单位长度至点A3 , …,按照这种移动方式进行下去,如果点An与原点的距离不小于20,那么n的最小值是________.
19.下面各正方形中的四个数之间都有相同的规律,则根据这种规律,第四个正方形中的n=________,最后一个正方形中的m=________.
三、计算题(共1题;共10分)
20.计算:
(1)(a2b)2 (2)(2x﹣1)2﹣x(2﹣x)
四、综合题(共3题;共36分)
21.综合题。
(1)12﹣(﹣18)+(﹣7)﹣15
(2)﹣22+3×(﹣1)4﹣(﹣4)×5
(3)3x2+6x+5﹣4x2+7x﹣6
(4)5(3a2b﹣ab2)﹣(ab2+3a2b)
22.(观察探索)用“<”、“>”或“=”完成以下填空,并观察两边算式,探索规律:
(1)
(2)(猜想证明)请用一个含字母a、b的式子表示上以规律,并证明结论的正确性;
(3)(应用拓展)比较代数式m2-3mn+1与mn-4n2的大小,并说明理由.
23.如图,把一个边长为a的正方形分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图①),再对其他8个小正方形作同样的分割(分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图②),继续同样的方法分割图形(图③),…得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样,它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”.求:
(1)图③中最新的一个最小正方形的边长;
(2)图③中所有涂黑部分的面积.
答 案
一、单选题
1.A 2. C 3. C 4. D 5. D 6. C 7. C 8.C 9. D 10. B 11.B 12.B
二、填空题
13.-3π 14. 15. (1)6×2;12×2(2)4n+n(n-1) ×2=2n2+2n
16. ;17. 28 18.13 19.10;212
三、计算题
20. (1)解: =a4b2 =a3b4
(2)解:(2x﹣1)2﹣x(2﹣x) =4x2﹣4x+1﹣2x+x2=5x2﹣6x+1
四、综合题
21. (1)解:原式=12+18﹣7﹣15=30﹣22=8
(2)解:原式=﹣4+3+20=19
(3)解:原式=﹣x2+13x﹣1
(4)解:原式=15a2b﹣5ab2﹣ab2﹣3a2b=12a2b﹣6ab2
22. (1)解:猜想:
2×(-3)×4=-24∴ 2×(-3)×4
=72
2×(-6)×(-6)=72∴ =2×(-6)×(-6)
(2)解:用字母表示这个规律:a2+b2≥2ab
证明: = -2ab+b2
又 ≥0
∴ -2ab+b2≥0∴a2+b2≥2ab
(3)解:
m2-3m+1-(mn-4n2)
=m2-3m+1-mn+4n2=m2-4mn+4n2+1=(m-2n)2+1∵(m-2n)2≥0∴(m-2n)2+1>0
所以m2-3m+1>mn-4n2
23. (1)解:观察图形的变化可知:
每分割一次,新的正方形的边长是上一个正方形的边长的 ,
所以图③中新的一个最小的正方形的边长为 a= a;
答:图③中新的一个最小正方形的边长为 a;
(2)解:观察图形的变化可知:
图①中,涂黑部分正方形的面积为 a,
图②中,涂黑部分所有正方形的面积为( )2a2= a2 ,
图③中,涂黑部分所有正方形的面积为( )3a2= a2 .
答:图③中,涂黑部分所有正方形的面积为 a2 .
(
第
- 1 -
页 共
7
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版七年级上册数学第二章测试题一(附答案)
一、单选题(共12题;共24分)
1.下列选项中,与xy2是同类项的是( )
A. -2xy2 B. 2x2y C. xy D. x2y2
2.下列说法正确的是( )
A. 不是单项式 B. 单项式 的系数是1 C. ﹣7ad的次数是2 D. 3x﹣2y不是多项式
3.下列运算正确的是( )
A. 7x-(-3x)=10 B. 5a+6b=11ab C. ab+2ba=3ab D. -(a-b)=a+b
4.计算的结果是( )
A. 6 B. C. 2 D.
5.如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A. (﹣1,0) B. (1,﹣2) C. (1,1) D. (﹣1,﹣1)
6.2010年广州亚运会吉祥物取名“乐羊羊”.图中各图是按照一定规律排列的羊的组图,图①有1只羊,图②有3只羊,……,则图⑩有( )只羊.
A. 53 B. 54 C. 55 D. 56
7.下列运算结果正确的是
A. B. C. D.
8.按一定规律排列的单项式:a,﹣a2 , a3 , ﹣a4 , a5 , ﹣a6 , ……,第n个单项式是( )
A. an B. ﹣an C. (﹣1)n+1an D. (﹣1)nan
9.下列说法中,不正确的是( )
A. ﹣ac的系数是﹣1,次数是4 B. ﹣1是整式
C. 6﹣3x+1的项是6、﹣3x,1 D. 2πR+π是三次二项式
10.实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )
A. 2a+b B. b C. -2a-b D. -b
11.如上图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,则点P第2017次跳动至P2017的坐标是( )
A. (504,1007) B. (505,1009) C. (1008,1007) D. (1009,1009)
12.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A. 4mcm B. 4ncm C. 2(m+n)cm D. 4(m-n)cm
二、填空题(共7题;共30分)
13.单项式-3πxyz2的系数是________.
14.以直线l外一点P为端点,向直线l上的 个点作射线,则以点P为顶点,以这些射线为边的角 小于 的个数为________ 用含有n的代数式表示
15.如图是由边长为1的木条组成的几何图案,观察图形规律,解决下列问题:
……….
(1)填空:第一个图案由1个正方形组成,共用的木条根数 ;
第二个图案由4个正方形组成,共用的木条根数 ;
第三个图案由9个正方形组成,共用的木条根数 ________;
第四个图案由16个正方形组成,共用的木条根数 ________;
(2)第 个图案由 个正方形组成,共用木条根数 ________(用含 的代数式表示)
16.如图,在平面直角坐标系中,已知点A(-4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(2)个三角形的直角顶点的坐标是________,第(2018)个三角形的直角顶点的坐标是________.
17.如图.乐乐班级举行“新春美食会”,同学们如图摆放桌椅,图(1)表示1张餐桌和6把椅子(三角形表示餐桌,每个小圆表示一把椅子),图(2)表示2张餐桌和8把椅子,图(3)表示3张餐桌和10把椅子,……;按照这种方式摆放12张餐桌,需要________把椅子.
18.如图,数轴上,点A的初始位置表示的数为1,现点A做如下移动:第1次点A向左移动3个单位长度至点A1 , 第2次从点A1向右移动6个单位长度至点A2 , 第3次从点A2向左移动9个单位长度至点A3 , …,按照这种移动方式进行下去,如果点An与原点的距离不小于20,那么n的最小值是________.
19.下面各正方形中的四个数之间都有相同的规律,则根据这种规律,第四个正方形中的n=________,最后一个正方形中的m=________.
三、计算题(共1题;共10分)
20.计算:
(1)(a2b)2 (2)(2x﹣1)2﹣x(2﹣x)
四、综合题(共3题;共36分)
21.综合题。
(1)12﹣(﹣18)+(﹣7)﹣15
(2)﹣22+3×(﹣1)4﹣(﹣4)×5
(3)3x2+6x+5﹣4x2+7x﹣6
(4)5(3a2b﹣ab2)﹣(ab2+3a2b)
22.(观察探索)用“<”、“>”或“=”完成以下填空,并观察两边算式,探索规律:
(1)
(2)(猜想证明)请用一个含字母a、b的式子表示上以规律,并证明结论的正确性;
(3)(应用拓展)比较代数式m2-3mn+1与mn-4n2的大小,并说明理由.
23.如图,把一个边长为a的正方形分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图①),再对其他8个小正方形作同样的分割(分成9个完全相同的小正方形,把最中间的一个小正方形涂成白色(图②),继续同样的方法分割图形(图③),…得到一些既复杂又漂亮的图形,它的每一部分放大,都和整体一模一样,它是波兰数学家谢尔宾斯基构造的,也被称为“谢尔宾斯基地毯”.求:
(1)图③中最新的一个最小正方形的边长;
(2)图③中所有涂黑部分的面积.
答 案
一、单选题
1.A 2. C 3. C 4. D 5. D 6. C 7. C 8.C 9. D 10. B 11.B 12.B
二、填空题
13.-3π 14. 15. (1)6×2;12×2(2)4n+n(n-1) ×2=2n2+2n
16. ;17. 28 18.13 19.10;212
三、计算题
20. (1)解: =a4b2 =a3b4
(2)解:(2x﹣1)2﹣x(2﹣x) =4x2﹣4x+1﹣2x+x2=5x2﹣6x+1
四、综合题
21. (1)解:原式=12+18﹣7﹣15=30﹣22=8
(2)解:原式=﹣4+3+20=19
(3)解:原式=﹣x2+13x﹣1
(4)解:原式=15a2b﹣5ab2﹣ab2﹣3a2b=12a2b﹣6ab2
22. (1)解:猜想:
2×(-3)×4=-24∴ 2×(-3)×4
=72
2×(-6)×(-6)=72∴ =2×(-6)×(-6)
(2)解:用字母表示这个规律:a2+b2≥2ab
证明: = -2ab+b2
又 ≥0
∴ -2ab+b2≥0∴a2+b2≥2ab
(3)解:
m2-3m+1-(mn-4n2)
=m2-3m+1-mn+4n2=m2-4mn+4n2+1=(m-2n)2+1∵(m-2n)2≥0∴(m-2n)2+1>0
所以m2-3m+1>mn-4n2
23. (1)解:观察图形的变化可知:
每分割一次,新的正方形的边长是上一个正方形的边长的 ,
所以图③中新的一个最小的正方形的边长为 a= a;
答:图③中新的一个最小正方形的边长为 a;
(2)解:观察图形的变化可知:
图①中,涂黑部分正方形的面积为 a,
图②中,涂黑部分所有正方形的面积为( )2a2= a2 ,
图③中,涂黑部分所有正方形的面积为( )3a2= a2 .
答:图③中,涂黑部分所有正方形的面积为 a2 .
(
第
- 1 -
页 共
7
页
)
