第五单元 圆 单元综合素质评价(含答案)人教版六年级上册数学
文档属性
| 名称 | 第五单元 圆 单元综合素质评价(含答案)人教版六年级上册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 771.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 15:41:44 | ||
图片预览


文档简介
单元综合素质评价
第五单元 圆
一 仔细推敲,选一选。(将正确答案的字母填在括号里)(每小题2 分,共24 分)
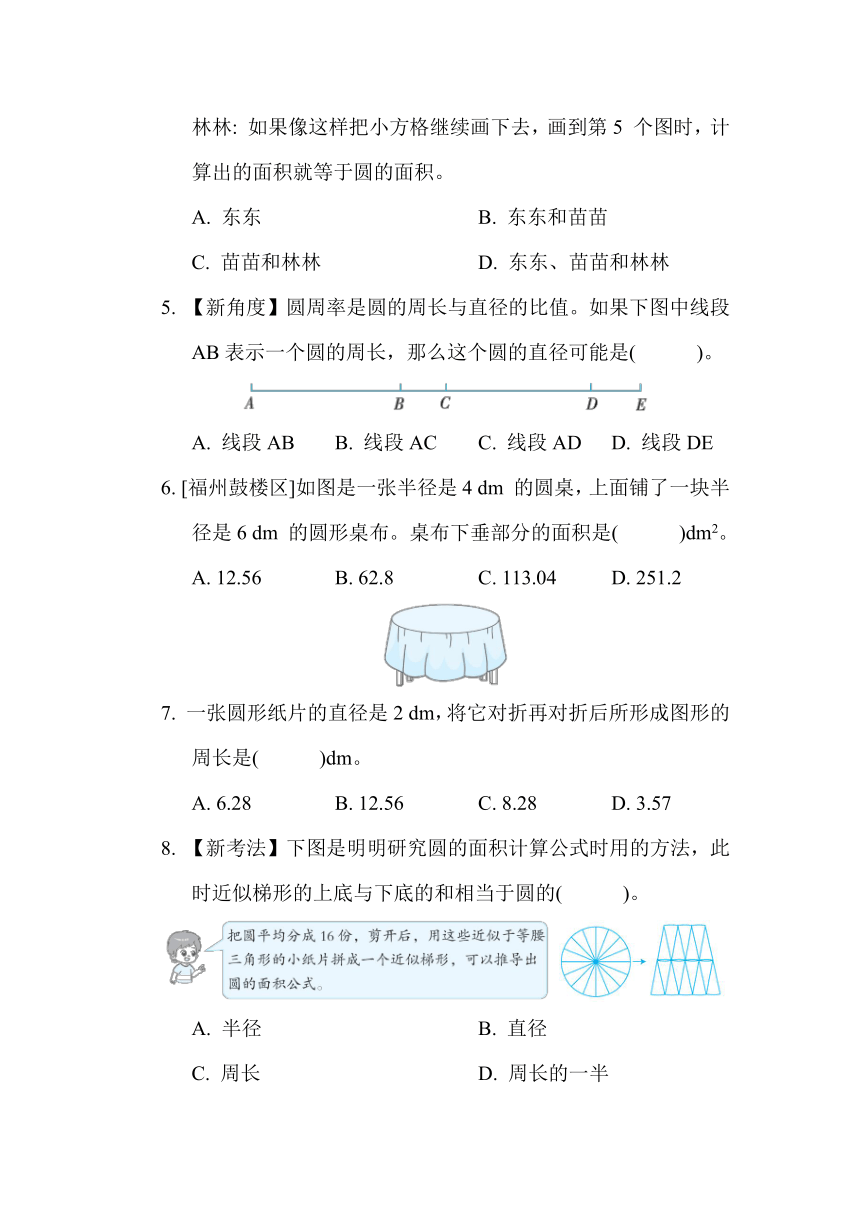
1. 下列图形中的∠1 属于圆心角的是( )。
2. [福州鼓楼区]下面各图中,对称轴条数最多的是( )。
3. 右图是一个残破的钟面,用软尺量得其边缘的弧长是9.42 cm,则它所在钟面的面积是( )cm2。
A. 9π B. 18π
C. 36π D. 144π
4. 【新考法】三位同学观察下图后说出了自己的想法,( )的想法正确。
东东: 研究圆的面积,可以用面积单位去测量。
苗苗: 如果小方格越来越小,那么求出来的小方格的面积就越来越接近圆的面积。
林林: 如果像这样把小方格继续画下去,画到第5 个图时,计算出的面积就等于圆的面积。
A. 东东 B. 东东和苗苗
C. 苗苗和林林 D. 东东、苗苗和林林
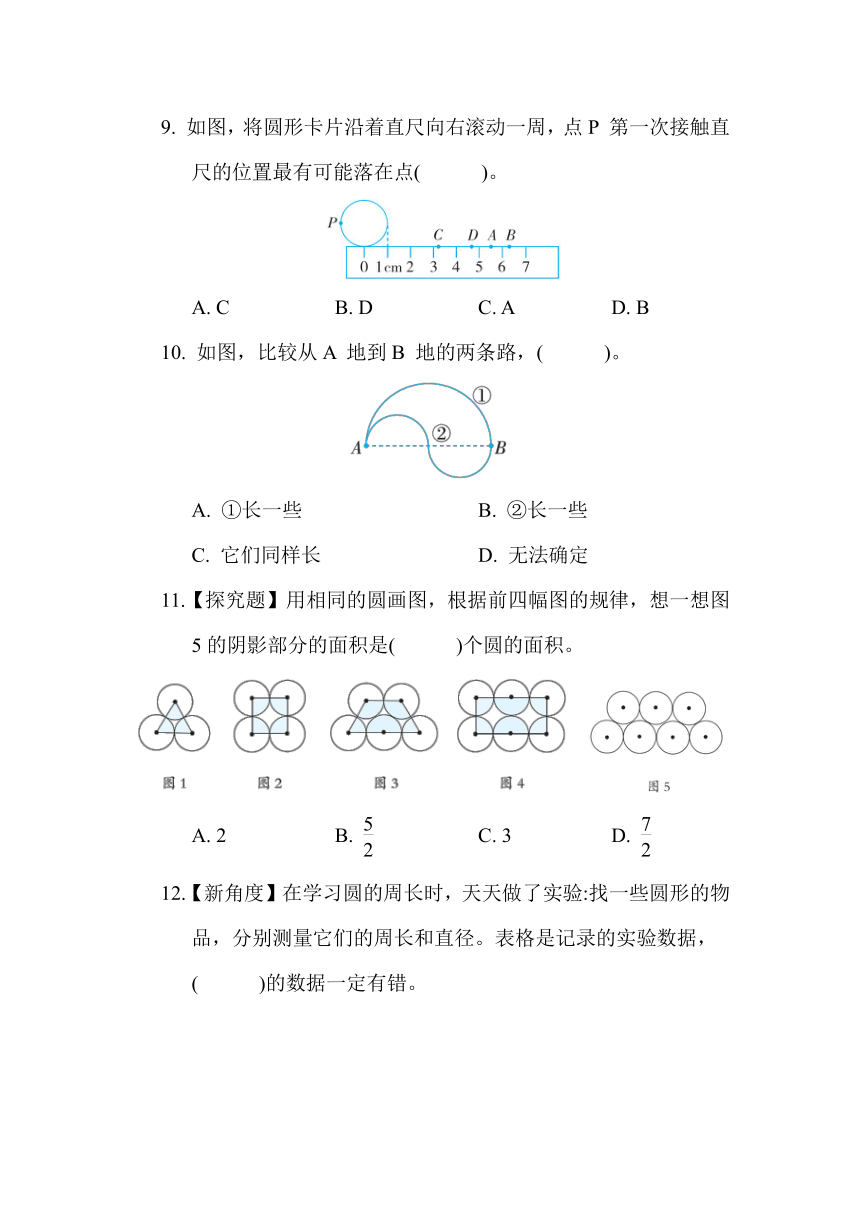
5. 【新角度】圆周率是圆的周长与直径的比值。如果下图中线段AB表示一个圆的周长,那么这个圆的直径可能是( )。
A. 线段AB B. 线段AC C. 线段AD D. 线段DE
6. [福州鼓楼区]如图是一张半径是4 dm 的圆桌,上面铺了一块半径是6 dm 的圆形桌布。桌布下垂部分的面积是( )dm2。
A. 12.56 B. 62.8 C. 113.04 D. 251.2
7. 一张圆形纸片的直径是2 dm,将它对折再对折后所形成图形的周长是( )dm。
A. 6.28 B. 12.56 C. 8.28 D. 3.57
8. 【新考法】下图是明明研究圆的面积计算公式时用的方法,此时近似梯形的上底与下底的和相当于圆的( )。
A. 半径 B. 直径
C. 周长 D. 周长的一半
9. 如图,将圆形卡片沿着直尺向右滚动一周,点P 第一次接触直尺的位置最有可能落在点( )。
A. C B. D C. A D. B
10. 如图,比较从A 地到B 地的两条路,( )。
A. ①长一些 B. ②长一些
C. 它们同样长 D. 无法确定
11.【探究题】用相同的圆画图,根据前四幅图的规律,想一想图5的阴影部分的面积是( )个圆的面积。
A. 2 B. C. 3 D.
12.【新角度】在学习圆的周长时,天天做了实验:找一些圆形的物品,分别测量它们的周长和直径。表格是记录的实验数据,( )的数据一定有错。
A. 硬币 B. 水杯 C. 蛋糕 D. 透明胶
二 认真审题,填一填。(每空1 分,共11 分)
1. 典典测量一个圆的直径是2 cm,则这个圆的周长是( )cm,面积是( )cm2。
2. 【新情境】大连永兴寺的千年银杏树被誉为“东北树王”。一根长25.12 m的麻绳刚好可以在这棵银杏树的树干上绕4 圈,这棵银杏树树干的横截面的半径是( )m,面积是( )m2。
3. 工人给儿童活动场地涂色分区,如右图。场地是边长为8 米的等边三角形,以顶点为圆心,以边长的一半为半径画弧,扇形区域涂蓝色(阴影部分),中间涂白色(空白部分),则中间白色部分的周长是( )米。
4. 一个近似圆形的人工湖,直径约是400 m,沿湖边每隔4 m 栽一棵树,一共要栽( )棵树。
5. 如图,以第一个圆的半径为直径画出第二个圆,再以第二个圆的半径为直径画出第三个圆,则第三个圆的面积(阴影部分)占第一个圆的面积的( )。
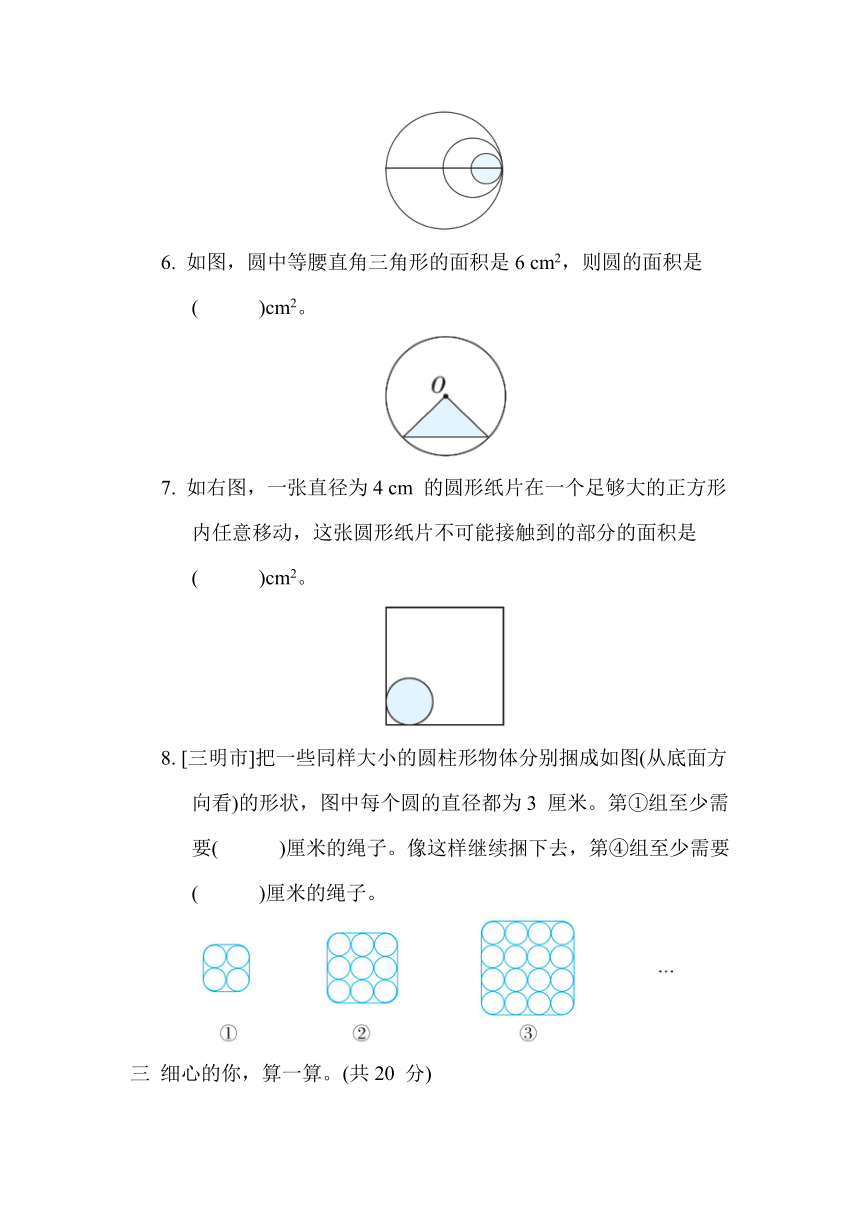
6. 如图,圆中等腰直角三角形的面积是6 cm2,则圆的面积是( )cm2。
7. 如右图,一张直径为4 cm 的圆形纸片在一个足够大的正方形内任意移动,这张圆形纸片不可能接触到的部分的面积是( )cm2。
8. [三明市]把一些同样大小的圆柱形物体分别捆成如图(从底面方向看)的形状,图中每个圆的直径都为3 厘米。第①组至少需要( )厘米的绳子。像这样继续捆下去,第④组至少需要( )厘米的绳子。
三 细心的你,算一算。(共20 分)
1. 求下面各圆的周长和面积。(每小题4 分,共8 分)
(1)d = 6 cm (2)r = 5 m
2. 求下面阴影部分的面积。(每小题4 分,共8 分)
(1) (2)
3. 已知图中正方形的面积是4 cm2 , 求阴影部分的面积。(4 分)
四 动手动脑,做一做。(共12 分)
1. [福州鼓楼区]如图,在方格纸中自己确定一点为圆心画一个圆,使A、B、C 三点都在圆上。(2 分)
2. (1)下面的图案你会画吗?请你用圆规在空白正方形中画一画。(2 分)
(2)若图中正方形的边长是4 cm,请你计算阴影部分的面积。(3 分)
3. 有理说理 已知圆的直径是20 cm,求这个圆的面积,华华根据圆的面积的推导过程(如下图),分步求结果。请你补充她计算的第三步,并说明理由。(5 分)
第一步:20÷2 = 10(cm)
第二步:π×10 = 10π(cm)
第三步:______________________________________________
理由:________________________________________________
_____________________________________________________
五 聪明的你,答一答。(共33 分)
1. 斐波那契螺旋线也称为黄金螺旋线,是自然界最完美的图案,它是用大小不同的圆心角为90°的扇形的弧线连起来的。第1 步扇形的半径是1 cm,按下图的方法画到第4 步,所得螺旋线的长是多少厘米?(6 分)
2. 为庆祝六一儿童节,厦门市阳光学校组织学生进行表演,表演舞台如下图。你能根据图中的数据计算出观众席的面积是多少平方米吗?(6 分)
3. [泉州鲤城区]公园里设计了一种“围树座椅”,形状如下图。
(1)天天紧紧绕着“围树座椅”的外围走一圈,走了多少米?(4 分)
(2)这种“围树座椅”椅面的面积有多少平方米?(5 分)
4. 如图,一只小狗拴在底面是边长为3 m 的等边三角形的建筑物的墙角,绳长4 m,这只小狗能看护的最大面积是多少平方米?(得数保留整数)(6 分)
5. 如图,一个运动场的两端是半圆形,中间是长方形。华华和同同进行跑步比赛,她们分别从A、B 两点出发,沿跑道线跑一圈,最后都回到终点。为了比赛公平,华华和同同的起跑线应相差多少米?(6 分)
答案
一1. C 2. C 3. C 4. B 5. D 6. B
7. D 8. D 9. B 10. C 11. B 12. B
二1. 6.28 3.14 2. 1 3.14
3. 12.56 4. 314 5.
6. 37.68 7. 3.44 8. 21.42 57.42
三1. (1)C = 3.14×6 = 18.84(cm)
S = 3.14×(6÷2)2 = 28.26(cm2)
(2) C = 3.14×5×2 = 31.4(m)
S = 3.14×52 = 78.5(m2)
2. (1)(3 + 5)×(3÷2)÷2 - 3.14×(3÷2)2÷2 = 2.4675(dm2)
(2)3×2 - ×3.14×22 -(3 - 2)×2÷2 = 1.86(cm2)
3. 4 - 3.14×4×= 0.86(cm2)
四1.
【点拨】根据圆的特点确定圆心的位置是关键。
2. (1)略
(2)4×4 - 3.14×(4÷2)2 = 3.44(cm2)
3. 10π×10 = 100π(cm2)
根据题意,将拼成的图形看成长方形,此时长方形的长为圆周长的一半(πr),宽为r,这样圆的面积就转化成了长方形的面积,即πr×r = πr2。
五1. 3.14×1×2×+ 3.14×1×2×2×+3.14×(1 + 1×2)×2×= 10.99(cm)
答:所得螺旋线的长是10.99 cm。
2. 20÷2 = 10(m) 10÷2 = 5(m)
5÷2 = 2.5 (m)
3.14×102÷2 - 3.14×52÷2 - 3.14×2.52÷2 =107.9375(m2)
答:观众席的面积是107.9375 m2。
3. (1)4×3.14 = 12.56(m)
答:走了12.56 m。
(2)4÷2 = 2(m) 2÷2 = 1(m)
3.14×(22 - 12) = 9.42(m2)
答:这种“围树座椅”椅面的面积有9.42 m2。
4. 4 - 3 = 1(m)
3.14×42×+ 3.14×12××2 ≈ 44(m2)
答:这只小狗能看护的最大面积是44 m2。
【点拨】依题意先画出草图,再计算。
5. 3.14×32×2 = 200.96(m)
3.14×(32 + 1)×2 = 207.24(m)
207.24 - 200.96 = 6.28(m)
答:华华和同同的起跑线应相差6.28 m。
【点拨】中间是长方形,长相等,只计算拐弯部分的差值就可以了。
第五单元 圆
一 仔细推敲,选一选。(将正确答案的字母填在括号里)(每小题2 分,共24 分)
1. 下列图形中的∠1 属于圆心角的是( )。
2. [福州鼓楼区]下面各图中,对称轴条数最多的是( )。
3. 右图是一个残破的钟面,用软尺量得其边缘的弧长是9.42 cm,则它所在钟面的面积是( )cm2。
A. 9π B. 18π
C. 36π D. 144π
4. 【新考法】三位同学观察下图后说出了自己的想法,( )的想法正确。
东东: 研究圆的面积,可以用面积单位去测量。
苗苗: 如果小方格越来越小,那么求出来的小方格的面积就越来越接近圆的面积。
林林: 如果像这样把小方格继续画下去,画到第5 个图时,计算出的面积就等于圆的面积。
A. 东东 B. 东东和苗苗
C. 苗苗和林林 D. 东东、苗苗和林林
5. 【新角度】圆周率是圆的周长与直径的比值。如果下图中线段AB表示一个圆的周长,那么这个圆的直径可能是( )。
A. 线段AB B. 线段AC C. 线段AD D. 线段DE
6. [福州鼓楼区]如图是一张半径是4 dm 的圆桌,上面铺了一块半径是6 dm 的圆形桌布。桌布下垂部分的面积是( )dm2。
A. 12.56 B. 62.8 C. 113.04 D. 251.2
7. 一张圆形纸片的直径是2 dm,将它对折再对折后所形成图形的周长是( )dm。
A. 6.28 B. 12.56 C. 8.28 D. 3.57
8. 【新考法】下图是明明研究圆的面积计算公式时用的方法,此时近似梯形的上底与下底的和相当于圆的( )。
A. 半径 B. 直径
C. 周长 D. 周长的一半
9. 如图,将圆形卡片沿着直尺向右滚动一周,点P 第一次接触直尺的位置最有可能落在点( )。
A. C B. D C. A D. B
10. 如图,比较从A 地到B 地的两条路,( )。
A. ①长一些 B. ②长一些
C. 它们同样长 D. 无法确定
11.【探究题】用相同的圆画图,根据前四幅图的规律,想一想图5的阴影部分的面积是( )个圆的面积。
A. 2 B. C. 3 D.
12.【新角度】在学习圆的周长时,天天做了实验:找一些圆形的物品,分别测量它们的周长和直径。表格是记录的实验数据,( )的数据一定有错。
A. 硬币 B. 水杯 C. 蛋糕 D. 透明胶
二 认真审题,填一填。(每空1 分,共11 分)
1. 典典测量一个圆的直径是2 cm,则这个圆的周长是( )cm,面积是( )cm2。
2. 【新情境】大连永兴寺的千年银杏树被誉为“东北树王”。一根长25.12 m的麻绳刚好可以在这棵银杏树的树干上绕4 圈,这棵银杏树树干的横截面的半径是( )m,面积是( )m2。
3. 工人给儿童活动场地涂色分区,如右图。场地是边长为8 米的等边三角形,以顶点为圆心,以边长的一半为半径画弧,扇形区域涂蓝色(阴影部分),中间涂白色(空白部分),则中间白色部分的周长是( )米。
4. 一个近似圆形的人工湖,直径约是400 m,沿湖边每隔4 m 栽一棵树,一共要栽( )棵树。
5. 如图,以第一个圆的半径为直径画出第二个圆,再以第二个圆的半径为直径画出第三个圆,则第三个圆的面积(阴影部分)占第一个圆的面积的( )。
6. 如图,圆中等腰直角三角形的面积是6 cm2,则圆的面积是( )cm2。
7. 如右图,一张直径为4 cm 的圆形纸片在一个足够大的正方形内任意移动,这张圆形纸片不可能接触到的部分的面积是( )cm2。
8. [三明市]把一些同样大小的圆柱形物体分别捆成如图(从底面方向看)的形状,图中每个圆的直径都为3 厘米。第①组至少需要( )厘米的绳子。像这样继续捆下去,第④组至少需要( )厘米的绳子。
三 细心的你,算一算。(共20 分)
1. 求下面各圆的周长和面积。(每小题4 分,共8 分)
(1)d = 6 cm (2)r = 5 m
2. 求下面阴影部分的面积。(每小题4 分,共8 分)
(1) (2)
3. 已知图中正方形的面积是4 cm2 , 求阴影部分的面积。(4 分)
四 动手动脑,做一做。(共12 分)
1. [福州鼓楼区]如图,在方格纸中自己确定一点为圆心画一个圆,使A、B、C 三点都在圆上。(2 分)
2. (1)下面的图案你会画吗?请你用圆规在空白正方形中画一画。(2 分)
(2)若图中正方形的边长是4 cm,请你计算阴影部分的面积。(3 分)
3. 有理说理 已知圆的直径是20 cm,求这个圆的面积,华华根据圆的面积的推导过程(如下图),分步求结果。请你补充她计算的第三步,并说明理由。(5 分)
第一步:20÷2 = 10(cm)
第二步:π×10 = 10π(cm)
第三步:______________________________________________
理由:________________________________________________
_____________________________________________________
五 聪明的你,答一答。(共33 分)
1. 斐波那契螺旋线也称为黄金螺旋线,是自然界最完美的图案,它是用大小不同的圆心角为90°的扇形的弧线连起来的。第1 步扇形的半径是1 cm,按下图的方法画到第4 步,所得螺旋线的长是多少厘米?(6 分)
2. 为庆祝六一儿童节,厦门市阳光学校组织学生进行表演,表演舞台如下图。你能根据图中的数据计算出观众席的面积是多少平方米吗?(6 分)
3. [泉州鲤城区]公园里设计了一种“围树座椅”,形状如下图。
(1)天天紧紧绕着“围树座椅”的外围走一圈,走了多少米?(4 分)
(2)这种“围树座椅”椅面的面积有多少平方米?(5 分)
4. 如图,一只小狗拴在底面是边长为3 m 的等边三角形的建筑物的墙角,绳长4 m,这只小狗能看护的最大面积是多少平方米?(得数保留整数)(6 分)
5. 如图,一个运动场的两端是半圆形,中间是长方形。华华和同同进行跑步比赛,她们分别从A、B 两点出发,沿跑道线跑一圈,最后都回到终点。为了比赛公平,华华和同同的起跑线应相差多少米?(6 分)
答案
一1. C 2. C 3. C 4. B 5. D 6. B
7. D 8. D 9. B 10. C 11. B 12. B
二1. 6.28 3.14 2. 1 3.14
3. 12.56 4. 314 5.
6. 37.68 7. 3.44 8. 21.42 57.42
三1. (1)C = 3.14×6 = 18.84(cm)
S = 3.14×(6÷2)2 = 28.26(cm2)
(2) C = 3.14×5×2 = 31.4(m)
S = 3.14×52 = 78.5(m2)
2. (1)(3 + 5)×(3÷2)÷2 - 3.14×(3÷2)2÷2 = 2.4675(dm2)
(2)3×2 - ×3.14×22 -(3 - 2)×2÷2 = 1.86(cm2)
3. 4 - 3.14×4×= 0.86(cm2)
四1.
【点拨】根据圆的特点确定圆心的位置是关键。
2. (1)略
(2)4×4 - 3.14×(4÷2)2 = 3.44(cm2)
3. 10π×10 = 100π(cm2)
根据题意,将拼成的图形看成长方形,此时长方形的长为圆周长的一半(πr),宽为r,这样圆的面积就转化成了长方形的面积,即πr×r = πr2。
五1. 3.14×1×2×+ 3.14×1×2×2×+3.14×(1 + 1×2)×2×= 10.99(cm)
答:所得螺旋线的长是10.99 cm。
2. 20÷2 = 10(m) 10÷2 = 5(m)
5÷2 = 2.5 (m)
3.14×102÷2 - 3.14×52÷2 - 3.14×2.52÷2 =107.9375(m2)
答:观众席的面积是107.9375 m2。
3. (1)4×3.14 = 12.56(m)
答:走了12.56 m。
(2)4÷2 = 2(m) 2÷2 = 1(m)
3.14×(22 - 12) = 9.42(m2)
答:这种“围树座椅”椅面的面积有9.42 m2。
4. 4 - 3 = 1(m)
3.14×42×+ 3.14×12××2 ≈ 44(m2)
答:这只小狗能看护的最大面积是44 m2。
【点拨】依题意先画出草图,再计算。
5. 3.14×32×2 = 200.96(m)
3.14×(32 + 1)×2 = 207.24(m)
207.24 - 200.96 = 6.28(m)
答:华华和同同的起跑线应相差6.28 m。
【点拨】中间是长方形,长相等,只计算拐弯部分的差值就可以了。
