数学人教A版(2019)选择性必修第一册2.1.2两条直线平行和垂直的判定 课件(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.1.2两条直线平行和垂直的判定 课件(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 552.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 17:44:10 | ||
图片预览





文档简介
(共18张PPT)
2.1.2
两条直线平行和垂直的判定
人教A版(2019)选择性必修第一册
学习目标
1. 能根据斜率判定两条直线平行或垂直。
2.理解直线平行或垂直的判定条件。
3.会运用两条直线平行或垂直来解决问题。
4.核心素养:逻辑推理、数学抽象、数学运算
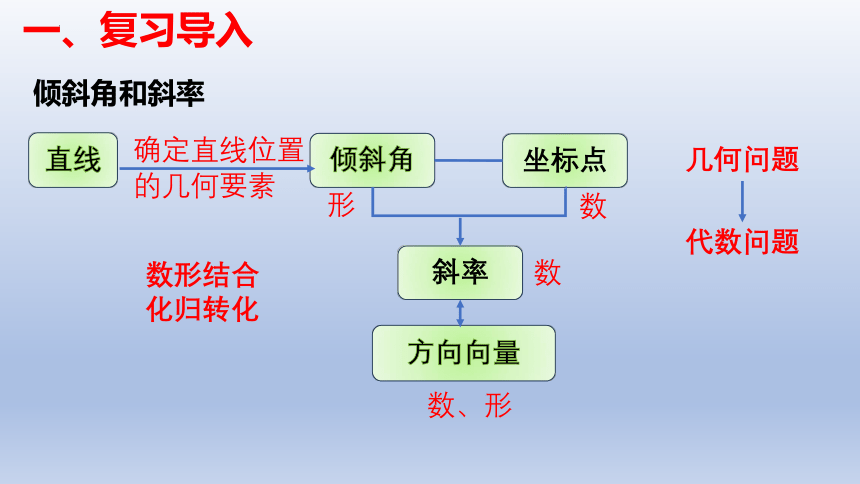
一、复习导入
直线
坐标点
倾斜角
方向向量
直线位置的几何要素
、形
斜率
数形结合
化归转化
几何问题
代数问题
倾斜角和斜率
二、新课讲授
1、两条直线平行
问题1:平面中两条直线有两种位置关系:相交、平行.当两条直线, 平行时,它们的斜率, 满足什么关系?
注:若没有特别说明,说“两条直线, ”时,指两条不重合的直线.
y
x
O
即 ,
形
数
反之,亦成立
故
追问1:上述关系,还有其他的证明方法吗?
y
x
O
设两条直线, 的斜率分别为, ,则直线, 的方向向量分别为=(1, ), =(1, ),于是:
1× 1× =0
于是,对于斜率分别为, 的两条直线, ,有:
追问2:当两条直线斜率不存在时,这两条直线是什么关系?
y
x
O
显然,当=90°时,直线, 的斜率不存在,此时
追问3:当两条直线重合时,它们的斜率有什么关系?
斜率证明三点共线时,常常用到这个结论.
y
x
O
A
B
C
共线
前提:斜率存在
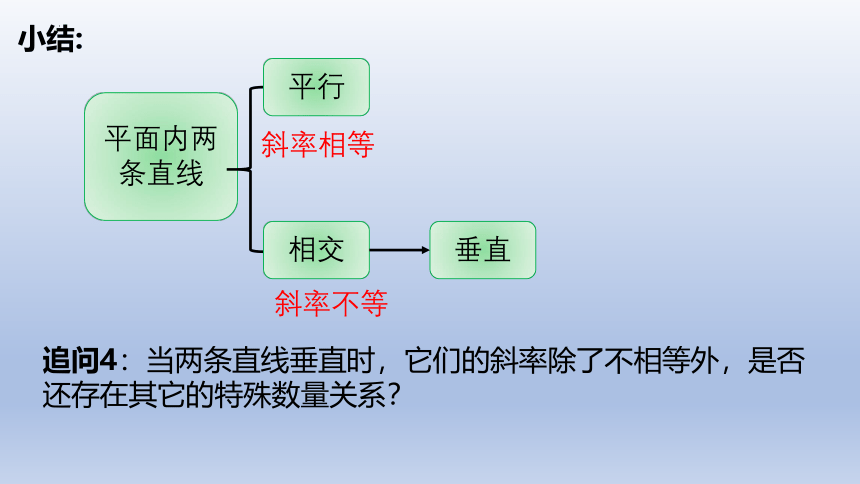
小结:
平面内两条直线
平行
相交
斜率相等
斜率不等
垂直
追问4:当两条直线垂直时,它们的斜率除了不相等外,是否还存在其它的特殊数量关系?
2、两条直线垂直
问题2:当两条直线垂直时,它们的斜率除了不相等外,是否还存在其它的特殊数量关系?
y
x
O
+90°
= = +90°)
=
追问1:上述关系,还有其他的证明方法吗?
设两条直线, 的斜率分别为, ,则直线, 的方向向量分别为=(1, ), =(1, ),于是:
追问1:上述关系,还有其他的证明方法吗?
=0
= 1
即 = 1
追问2:当直线或 倾斜角为90°时,若则另一条直线的倾斜角为多少?
y
x
O
显然,当=90°时, =0°.反之亦然.
三、巩固新知
例2 已知A(2,3),B(4,0),P (3,1), P (1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
分析:
1、画出两条直线
2、判断两条直线的位置关系
3、判断两条直线的斜率是否存在
4、判断斜率是否相等
解:如图,直线BA的斜率==
直线PQ的斜率==
因为 ,所以直线AB PQ.
y
x
O
A
P
B
Q
例3 已知四边形ABCD的四个顶点分别为A(0,0),B(2,–1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
y
x
O
A
B
C
D
解:如图,由已知可得
AB边所在直线的斜率==-
CD边所在直线的斜率==-
BC边所在直线的斜率==
DA边所在直线的斜率==
因为, = ,所以直线AB CD, BC DA.
因此,四边形ABCD是平行四边形.
例4 已知A(6,0),B(),P (), Q (6, ),试判断直线AB与PQ的位置关系,并证明你的结论.
解:直线AB的斜率==
直线PQ的斜率==-
因为 = ×(-)= 1,所以直线AB PQ.
例5 已知A(5, ),B(),C()三点,试判断△ABC的形状.
A
B
C
y
x
O
解:如图,由已知可得
AB边所在直线的斜率==-
BC边所在直线的斜率==
因为=-×2= 1,所以直线AB BC,即∠ABC=90°.
所以,△ABC是直角三角形.
变式训练 已知A(5, ),C()三点,点B在x轴上,且∠ABC为直角,求点B的坐标.
分析:
1、设B(x,0)
2、计算,
3、根据 1,构造方程
解:设B(x,0)
则== , ==
当x≠5且x≠2时, = × = 1
当x=5或x=2时,∠ABC均不为直角.
整理,得x 7x+7=0
解得 x或x
四、课堂小结
1. .
2. = 1.
五、作业布置
课本P57:练习 第2题
几何问题
代数问题
代数问题的解
几何问题的解
2.1.2
两条直线平行和垂直的判定
人教A版(2019)选择性必修第一册
学习目标
1. 能根据斜率判定两条直线平行或垂直。
2.理解直线平行或垂直的判定条件。
3.会运用两条直线平行或垂直来解决问题。
4.核心素养:逻辑推理、数学抽象、数学运算
一、复习导入
直线
坐标点
倾斜角
方向向量
直线位置的几何要素
、形
斜率
数形结合
化归转化
几何问题
代数问题
倾斜角和斜率
二、新课讲授
1、两条直线平行
问题1:平面中两条直线有两种位置关系:相交、平行.当两条直线, 平行时,它们的斜率, 满足什么关系?
注:若没有特别说明,说“两条直线, ”时,指两条不重合的直线.
y
x
O
即 ,
形
数
反之,亦成立
故
追问1:上述关系,还有其他的证明方法吗?
y
x
O
设两条直线, 的斜率分别为, ,则直线, 的方向向量分别为=(1, ), =(1, ),于是:
1× 1× =0
于是,对于斜率分别为, 的两条直线, ,有:
追问2:当两条直线斜率不存在时,这两条直线是什么关系?
y
x
O
显然,当=90°时,直线, 的斜率不存在,此时
追问3:当两条直线重合时,它们的斜率有什么关系?
斜率证明三点共线时,常常用到这个结论.
y
x
O
A
B
C
共线
前提:斜率存在
小结:
平面内两条直线
平行
相交
斜率相等
斜率不等
垂直
追问4:当两条直线垂直时,它们的斜率除了不相等外,是否还存在其它的特殊数量关系?
2、两条直线垂直
问题2:当两条直线垂直时,它们的斜率除了不相等外,是否还存在其它的特殊数量关系?
y
x
O
+90°
= = +90°)
=
追问1:上述关系,还有其他的证明方法吗?
设两条直线, 的斜率分别为, ,则直线, 的方向向量分别为=(1, ), =(1, ),于是:
追问1:上述关系,还有其他的证明方法吗?
=0
= 1
即 = 1
追问2:当直线或 倾斜角为90°时,若则另一条直线的倾斜角为多少?
y
x
O
显然,当=90°时, =0°.反之亦然.
三、巩固新知
例2 已知A(2,3),B(4,0),P (3,1), P (1,2),试判断直线AB与PQ的位置关系,并证明你的结论.
分析:
1、画出两条直线
2、判断两条直线的位置关系
3、判断两条直线的斜率是否存在
4、判断斜率是否相等
解:如图,直线BA的斜率==
直线PQ的斜率==
因为 ,所以直线AB PQ.
y
x
O
A
P
B
Q
例3 已知四边形ABCD的四个顶点分别为A(0,0),B(2,–1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明.
y
x
O
A
B
C
D
解:如图,由已知可得
AB边所在直线的斜率==-
CD边所在直线的斜率==-
BC边所在直线的斜率==
DA边所在直线的斜率==
因为, = ,所以直线AB CD, BC DA.
因此,四边形ABCD是平行四边形.
例4 已知A(6,0),B(),P (), Q (6, ),试判断直线AB与PQ的位置关系,并证明你的结论.
解:直线AB的斜率==
直线PQ的斜率==-
因为 = ×(-)= 1,所以直线AB PQ.
例5 已知A(5, ),B(),C()三点,试判断△ABC的形状.
A
B
C
y
x
O
解:如图,由已知可得
AB边所在直线的斜率==-
BC边所在直线的斜率==
因为=-×2= 1,所以直线AB BC,即∠ABC=90°.
所以,△ABC是直角三角形.
变式训练 已知A(5, ),C()三点,点B在x轴上,且∠ABC为直角,求点B的坐标.
分析:
1、设B(x,0)
2、计算,
3、根据 1,构造方程
解:设B(x,0)
则== , ==
当x≠5且x≠2时, = × = 1
当x=5或x=2时,∠ABC均不为直角.
整理,得x 7x+7=0
解得 x或x
四、课堂小结
1. .
2. = 1.
五、作业布置
课本P57:练习 第2题
几何问题
代数问题
代数问题的解
几何问题的解
