沪教版(五四学制)九年级数学上册25.3解直角三角形
文档属性
| 名称 | 沪教版(五四学制)九年级数学上册25.3解直角三角形 |
|
|
| 格式 | doc | ||
| 文件大小 | 118.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 20:44:48 | ||
图片预览

文档简介
25.3解直角三角形
一、教学内容分析
本课时其实是安排了一个解直角三角形和应用的一节过度课,它起到了承上启下的作用.先从解一般的三角形或梯形的问题,寻找转化为直角三角形的方法,然后,到下一节课的应用,使学生不会有知识过度跳跃的感觉.
二、教学目标设计
1.进一步运用勾股定理、锐角三角比解非直角三角形.
2. 通过综合运用锐角三角比解三角形,逐步形成分析问题、解决问题的能力.
三、教学重点及难点
教学重点:学会把一般三角形转化为直角三角形解决.
教学难点:如何转化为直角三角形的辅助线的做法.
四、教学用具准备
三角尺、实物投影仪、多媒体设备.
五、教学过程设计
一、 情景引入
1.复习
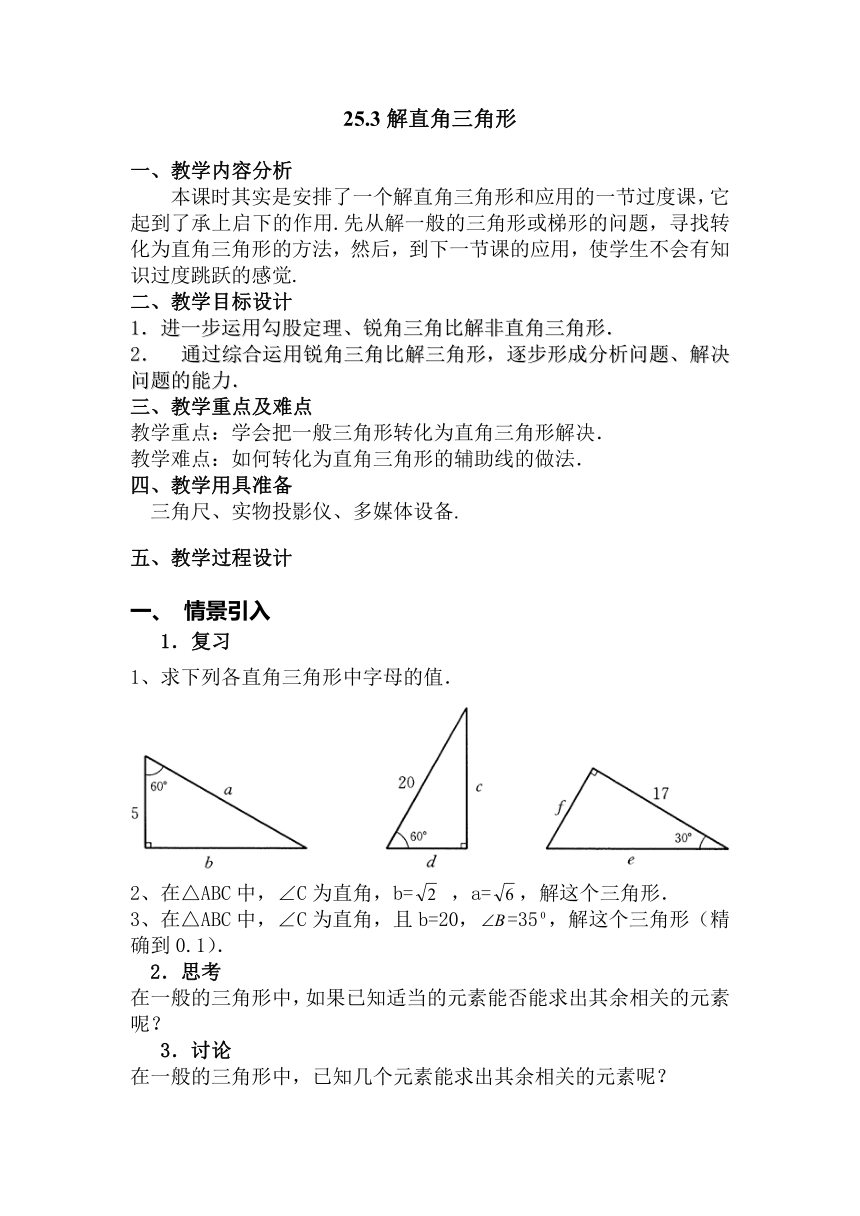
1、求下列各直角三角形中字母的值.
2、在△ABC中,∠C为直角,b= ,a=,解这个三角形.
3、在△ABC中,∠C为直角,且b=20,=35,解这个三角形(精确到0.1).
2.思考
在一般的三角形中,如果已知适当的元素能否能求出其余相关的元素呢?
3.讨论
在一般的三角形中,已知几个元素能求出其余相关的元素呢?
二、学习新课
1.例题分析
例题1 在等腰三角形ABC中,已知AB=AC, ∠A=45°,BC=6,求它的腰长和底角.
分析:根据三角形内角和定理,可求得底角的大小.如图,作底边上的高,由等腰三角形“三线合一”的性质,可知底边被高平分,于是得到两个全等的直角三角形.因此在其中任意一个直角三角形中,知道了一个锐角、一条直角边,可解这个直角三角形,从而得到等腰三角形的腰长.
解: 在△ABC中,
∠B= ∠C= (1800-∠A)
= (1800-450)=67.50=67030’
过点A作AD⊥BC,垂足为点D
∵ AB=AC,
∴BD=BC=×6=3
在Rt△ABD中
∵cosB=
∴AB=
所以,这个等腰三角形的腰长约为7.839,底角为67030’.
思考:本题如果作腰上的高,能解△ABC吗?
试一试:在等腰三角形中,已知AB=AC=5,BC=6,求它的顶角和底角.
例题2 在△ABC中,AC=9,AB=8.5,∠A=38°,求AC边上的高及△ABC的面积.
分析:为了利用∠A的三角比,所以作出AC或AB边上的高,构造直角三角形,可求出一条高,再求出三角形的面积.
解:过点B作BD⊥AC,垂足为D.
在Rt△ABD中,∵sinA=,
∴ BD=AB·sinA=8.5×sin38°≈5.233
S△ABC=AC·BD=×9×5.233≈23.55
所以,AC边上的高约为5.233,△ABC的面积约为23.55.
2.问题拓展
例题3 如图,在⊿ABC中,∠A=30°,tanB=,AC=2,求AB
分析:本题可以过点C作AB边的垂线,把∠A和∠B作在直角三角形中,再利用锐角三角比解决问题.教师引导学生解答.
四、课堂小结
本节课我们利用直角三角形的知识将某些一般三角形问题或梯形问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.今后,我们还要善于用数学知识解决实际问题.
五、作业布置
练习册25.3(2)
D
B
C
A
A
C
B
一、教学内容分析
本课时其实是安排了一个解直角三角形和应用的一节过度课,它起到了承上启下的作用.先从解一般的三角形或梯形的问题,寻找转化为直角三角形的方法,然后,到下一节课的应用,使学生不会有知识过度跳跃的感觉.
二、教学目标设计
1.进一步运用勾股定理、锐角三角比解非直角三角形.
2. 通过综合运用锐角三角比解三角形,逐步形成分析问题、解决问题的能力.
三、教学重点及难点
教学重点:学会把一般三角形转化为直角三角形解决.
教学难点:如何转化为直角三角形的辅助线的做法.
四、教学用具准备
三角尺、实物投影仪、多媒体设备.
五、教学过程设计
一、 情景引入
1.复习
1、求下列各直角三角形中字母的值.
2、在△ABC中,∠C为直角,b= ,a=,解这个三角形.
3、在△ABC中,∠C为直角,且b=20,=35,解这个三角形(精确到0.1).
2.思考
在一般的三角形中,如果已知适当的元素能否能求出其余相关的元素呢?
3.讨论
在一般的三角形中,已知几个元素能求出其余相关的元素呢?
二、学习新课
1.例题分析
例题1 在等腰三角形ABC中,已知AB=AC, ∠A=45°,BC=6,求它的腰长和底角.
分析:根据三角形内角和定理,可求得底角的大小.如图,作底边上的高,由等腰三角形“三线合一”的性质,可知底边被高平分,于是得到两个全等的直角三角形.因此在其中任意一个直角三角形中,知道了一个锐角、一条直角边,可解这个直角三角形,从而得到等腰三角形的腰长.
解: 在△ABC中,
∠B= ∠C= (1800-∠A)
= (1800-450)=67.50=67030’
过点A作AD⊥BC,垂足为点D
∵ AB=AC,
∴BD=BC=×6=3
在Rt△ABD中
∵cosB=
∴AB=
所以,这个等腰三角形的腰长约为7.839,底角为67030’.
思考:本题如果作腰上的高,能解△ABC吗?
试一试:在等腰三角形中,已知AB=AC=5,BC=6,求它的顶角和底角.
例题2 在△ABC中,AC=9,AB=8.5,∠A=38°,求AC边上的高及△ABC的面积.
分析:为了利用∠A的三角比,所以作出AC或AB边上的高,构造直角三角形,可求出一条高,再求出三角形的面积.
解:过点B作BD⊥AC,垂足为D.
在Rt△ABD中,∵sinA=,
∴ BD=AB·sinA=8.5×sin38°≈5.233
S△ABC=AC·BD=×9×5.233≈23.55
所以,AC边上的高约为5.233,△ABC的面积约为23.55.
2.问题拓展
例题3 如图,在⊿ABC中,∠A=30°,tanB=,AC=2,求AB
分析:本题可以过点C作AB边的垂线,把∠A和∠B作在直角三角形中,再利用锐角三角比解决问题.教师引导学生解答.
四、课堂小结
本节课我们利用直角三角形的知识将某些一般三角形问题或梯形问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.今后,我们还要善于用数学知识解决实际问题.
五、作业布置
练习册25.3(2)
D
B
C
A
A
C
B
