北师大版数学 七年级下册第三章 变量之间的关系:3.1 用表格表示变量之间的关系 教学设计(表格式)(无答案)
文档属性
| 名称 | 北师大版数学 七年级下册第三章 变量之间的关系:3.1 用表格表示变量之间的关系 教学设计(表格式)(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 54.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 00:00:00 | ||
图片预览


文档简介
《用表格表示变量之间的关系》教学设计
课 题 用表格表示变量之间的关系 课 型 新授课 第1课时
教学目标 知识与技能 理解什么是变量,自变量,因变量。 能从表格中获取变量之间关系的信息,并能用表格表示两个变量之间的关系。
过程与方法 经历探索具体情境中两个变量之间的关系的过程。 通过从表格中分析两个变量之间的关系,并用自己的语言进行表述,发展学生有条理地思考和表达的能力。
情感态度与价值观 经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感,增强学习数学的成就感,发展学生对数学的认识
教学重点 经历探索具体情境中两个变量之间关系的过程,理解变量,自变量,因变量,能从表格中获取变量之间关系的信息,能用表格表示两个变量之间的关系,并能根据表格中的数据尝试对变化的趋势进行初步的预测。
教学难点 在探索活动中理解变量之间的相依关系,并尝试永语言和符号去刻画,根据表格中的数据对变化的趋势进行初步预测。
教与学策略 观察、演示实验、讨论
课前准备(教具、活动准备等) 制作季节变化和色彩变化的图片及小车在木板上下滑的动画,我国从1949年到2008年的人口统计表
教 学 过 程
教学步骤 教 师 活 动 学 生 活 动 设 计 意 图
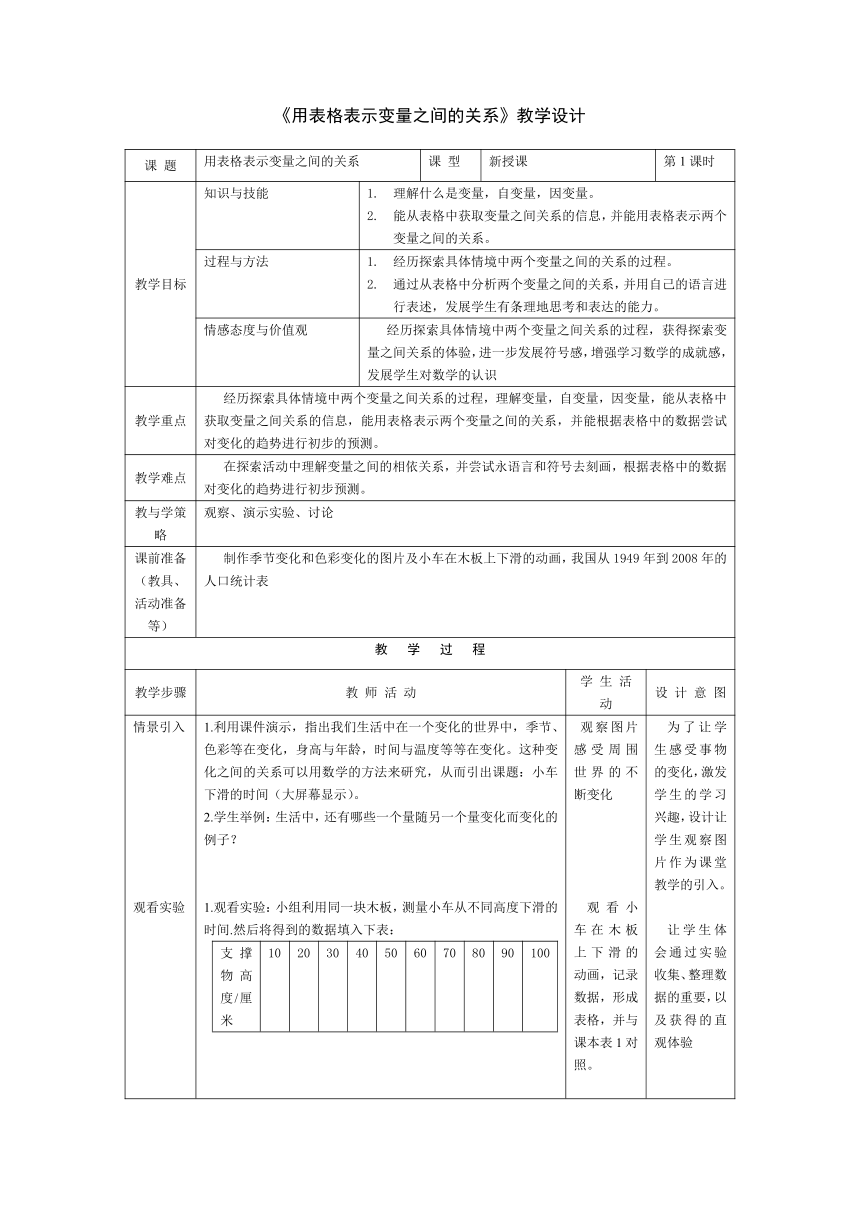
情景引入 观看实验 合作探究 概念介绍 练习提高 归纳总结 目标检测 布置作业 1.利用课件演示,指出我们生活中在一个变化的世界中,季节、色彩等在变化,身高与年龄,时间与温度等等在变化。这种变化之间的关系可以用数学的方法来研究,从而引出课题:小车下滑的时间(大屏幕显示)。 2.学生举例:生活中,还有哪些一个量随另一个量变化而变化的例子? 1.观看实验:小组利用同一块木板,测量小车从不同高度下滑的时间.然后将得到的数据填入下表: 支撑物高度/厘米102030405060708090100小车下滑时间/秒
2.对照课本的表1,讨论交流下列问题: (1)支撑物高度为70厘米时,小车下滑的时间是多少? (2)如果用h表示支撑物高度,t表示小车下滑的时间,随着h逐渐变大,t 的变化趋势是什么? (3)h每增加10厘米,t的变化情况相同吗? (4)估计当h=110厘米时,t的值是多少?你是怎样估计的? 3、演示课件——当高度为10、20、30厘米时小车下滑的时间. 根据做的实验和经验,解释为什么会有支撑物h越高,小车下滑时间t越短呢? 4.由以上问题串可知,h和t是两个变化的数量,而h的每一次变化,都会引起t的变化,下滑时间和支撑物高度之间存在着相依关系. 5、讨论交流从课本表2中获得的信息并回答下列问题: 时间/年194919591969197919891999人口/亿5.426.728.079.7511.0712.59
(1)如果用 x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么? (2)从1949年起,时间每向后推移10年,我国人口是怎样变化的? (3)估计到2009年,我国人口总数是多少? 6、师生共同总结两个变化过程中发生变化的量,区分自变量和因变量。 出示题组练习 提问学生谈一下这节课的收获,引导学生从本节课学到的内容和学习方法上去进行归纳总结。 出示检测题,学生做完后出示答案 习题1、2题 2、活动与探究 在北京市“危旧房改造”中,小强一家搬进了回龙观小区.这个小区冬季用家庭燃气炉取暖.为了估算冬季取暖第一个月使用天然气的开支情况,从11月15日起,小强连续八天每天晚上记录了天然气表显示的读数,如下表〔注:天然气表中先后两次显示的读数之差就是这段时间内使用天然气的数量(单位:m3)〕 日期1516171819202122表的读数220229241249259270279290
小强的妈妈11月15日买了一张面值600元的天然气使用卡,已知每立方米天然气1.70元,请你估算这张卡够小强家用一个月(按30天计算)吗?为什么? 观察图片感受周围世界的不断变化 观看小车在木板上下滑的动画,记录数据,形成表格,并与课本表1对照。 独立思考,然后用自己的语言阐述思考过程及理由. 积极回答问题 初步认识变量,了解它们之间是相依的关系 讨论并回答问题 在老师的引导下理解变量、自变量、因变量的概念 做题组练习 谈这节课的收获 做检测题并对照答案 为了让学生感受事物的变化,激发学生的学习兴趣,设计让学生观察图片作为课堂教学的引入。 让学生体会通过实验收集、整理数据的重要,以及获得的直观体验 关注学生是否积极地进行活动,并在活动中独立思考;能否意识到变量之间的相依关系;能否运用自己的语言描述这种关系等 让学生进一步体会变量之间的关系,学习如何从表格中获取信息,发展学生通过数据分析进行预测的能力。并让学生体会“此时字母表示的是变量”,以进一步发展学生对“字母表示”的理解 培养学生有条理地思考和表达的能力 巩固所学知识,注重知识的应用,加深对变量之间关系的理解。 注重在学生的浓厚兴趣和主动积极的思维活动及具体情境中对变量等概念的反馈和理解。
附板书设计: 小车下滑的时间 1.①支撑物h越高,小车下滑时间t越短; ②随着时间x的增加,我国人口总数y增加. 其中h和t,x和y都是变量.①中h是自变量,t是因变量;②中x是自变量,y是因变量. 2.借助表格,可以表示因变量随自变量的变化而变化的情况.
教后反思:
题组练习:
A 、某河受暴雨袭击,某天此河水的水位记录为下表:
时间/小时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
依据此表回答下列问题:
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
B、(p165)研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量(千克/公顷) 0 34 67 101 135 202 259 336 404 471
土豆产量 (吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75
依据此表回答下列问题:
(1)此表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说一说你的理由。
(4)粗略说一说氮肥的施用量对土豆产量的影响。
C、某婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,5周岁、10周岁时的体重分别大约是1周岁时的2倍、3倍。
上述哪两个量在变化?自变量和因变量各是什么?
某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
年龄 刚出生 6个月 1周岁 2周岁 5周岁 10周岁
体重/千克
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的。
目标检测:
训练平台
一个专卖香蕉的水果小贩,每千克香蕉卖3、5元,某日他忘了带计算器,给算账带来不便,于是他通过笔算在硬纸板上作了一个表格,使他在算账时只需作简单的加法就可以了,表格如下:
重量/千克 0、05 0、1 0、15 0、2 0、25 0、3 0、35 0、4 0、45 0、5
价格/元 0、18 0、35 0、53 0、7 0、88 1、05 1、23 1、4 1、58 1、75
当买香蕉0、5千克时,价格是多少?
如果用x表示质量,y表示价格,那么x随着的变化,y的变化趋势时什么?
请你估计当x=3千克时,y的值是多少?
爷爷告诉小强:“距离地面越高,温度越低”,并给小强出示了下面的表格:
距离地面高度/千米 0 1 2 3 4 5
温度/摄氏度 20 14 8 2 —4 —10
根据上表,爷爷还给小强出了下面几个问题,请你和小强一起来回答。
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎样变化的?
你知道距离地面5千米的高空温度是多少?
你能猜出距离地面6千米的高空温度是多少?
提高训练
你知道地球上的人口数量是怎样变化的吗?请看下表:
时间/年 1600 1830 1930 1960 1974 1987 1999
人口数量/亿 5 10 20 30 40 50 60
现在你清楚了吧,根据上表,请回答下列问题:
上表的哪些量在发生变化?自变量和因变量各是什么?
如果用x表示时间,y表示地球上人口总数,那么随着x的变化,y的变化趋势是什么?
从1930年起,时间向后推移30年,世界人口数量变化了吗?变化了多少?
探索发现
杨嫂再就业中心的扶持下,创办了“润物”报刊零售点,对经营的某种晚报,杨嫂提供了如下信息:(1)买进一份0、02元,卖出一份0、30元;(2)一个月内(以30天计),有20天每天可以卖出200份,其余10天每天只能卖出120份;(3)一个月内,每天从报社买进的报纸份数必须相同。当天卖不掉的报纸,以每份0、10元退给报社。
一个月内每天买进该种晚报的份数分别为100份和150份时,月利润(单位:元)是多少?
上述的哪些量在发生变化?自变量和因变量各是多少/
设每天从报社买进该种晚报x份(120≤x≤200),月利润为元,请写出y与x的关系式,并确定月利润的最大值
课 题 用表格表示变量之间的关系 课 型 新授课 第1课时
教学目标 知识与技能 理解什么是变量,自变量,因变量。 能从表格中获取变量之间关系的信息,并能用表格表示两个变量之间的关系。
过程与方法 经历探索具体情境中两个变量之间的关系的过程。 通过从表格中分析两个变量之间的关系,并用自己的语言进行表述,发展学生有条理地思考和表达的能力。
情感态度与价值观 经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感,增强学习数学的成就感,发展学生对数学的认识
教学重点 经历探索具体情境中两个变量之间关系的过程,理解变量,自变量,因变量,能从表格中获取变量之间关系的信息,能用表格表示两个变量之间的关系,并能根据表格中的数据尝试对变化的趋势进行初步的预测。
教学难点 在探索活动中理解变量之间的相依关系,并尝试永语言和符号去刻画,根据表格中的数据对变化的趋势进行初步预测。
教与学策略 观察、演示实验、讨论
课前准备(教具、活动准备等) 制作季节变化和色彩变化的图片及小车在木板上下滑的动画,我国从1949年到2008年的人口统计表
教 学 过 程
教学步骤 教 师 活 动 学 生 活 动 设 计 意 图
情景引入 观看实验 合作探究 概念介绍 练习提高 归纳总结 目标检测 布置作业 1.利用课件演示,指出我们生活中在一个变化的世界中,季节、色彩等在变化,身高与年龄,时间与温度等等在变化。这种变化之间的关系可以用数学的方法来研究,从而引出课题:小车下滑的时间(大屏幕显示)。 2.学生举例:生活中,还有哪些一个量随另一个量变化而变化的例子? 1.观看实验:小组利用同一块木板,测量小车从不同高度下滑的时间.然后将得到的数据填入下表: 支撑物高度/厘米102030405060708090100小车下滑时间/秒
2.对照课本的表1,讨论交流下列问题: (1)支撑物高度为70厘米时,小车下滑的时间是多少? (2)如果用h表示支撑物高度,t表示小车下滑的时间,随着h逐渐变大,t 的变化趋势是什么? (3)h每增加10厘米,t的变化情况相同吗? (4)估计当h=110厘米时,t的值是多少?你是怎样估计的? 3、演示课件——当高度为10、20、30厘米时小车下滑的时间. 根据做的实验和经验,解释为什么会有支撑物h越高,小车下滑时间t越短呢? 4.由以上问题串可知,h和t是两个变化的数量,而h的每一次变化,都会引起t的变化,下滑时间和支撑物高度之间存在着相依关系. 5、讨论交流从课本表2中获得的信息并回答下列问题: 时间/年194919591969197919891999人口/亿5.426.728.079.7511.0712.59
(1)如果用 x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是什么? (2)从1949年起,时间每向后推移10年,我国人口是怎样变化的? (3)估计到2009年,我国人口总数是多少? 6、师生共同总结两个变化过程中发生变化的量,区分自变量和因变量。 出示题组练习 提问学生谈一下这节课的收获,引导学生从本节课学到的内容和学习方法上去进行归纳总结。 出示检测题,学生做完后出示答案 习题1、2题 2、活动与探究 在北京市“危旧房改造”中,小强一家搬进了回龙观小区.这个小区冬季用家庭燃气炉取暖.为了估算冬季取暖第一个月使用天然气的开支情况,从11月15日起,小强连续八天每天晚上记录了天然气表显示的读数,如下表〔注:天然气表中先后两次显示的读数之差就是这段时间内使用天然气的数量(单位:m3)〕 日期1516171819202122表的读数220229241249259270279290
小强的妈妈11月15日买了一张面值600元的天然气使用卡,已知每立方米天然气1.70元,请你估算这张卡够小强家用一个月(按30天计算)吗?为什么? 观察图片感受周围世界的不断变化 观看小车在木板上下滑的动画,记录数据,形成表格,并与课本表1对照。 独立思考,然后用自己的语言阐述思考过程及理由. 积极回答问题 初步认识变量,了解它们之间是相依的关系 讨论并回答问题 在老师的引导下理解变量、自变量、因变量的概念 做题组练习 谈这节课的收获 做检测题并对照答案 为了让学生感受事物的变化,激发学生的学习兴趣,设计让学生观察图片作为课堂教学的引入。 让学生体会通过实验收集、整理数据的重要,以及获得的直观体验 关注学生是否积极地进行活动,并在活动中独立思考;能否意识到变量之间的相依关系;能否运用自己的语言描述这种关系等 让学生进一步体会变量之间的关系,学习如何从表格中获取信息,发展学生通过数据分析进行预测的能力。并让学生体会“此时字母表示的是变量”,以进一步发展学生对“字母表示”的理解 培养学生有条理地思考和表达的能力 巩固所学知识,注重知识的应用,加深对变量之间关系的理解。 注重在学生的浓厚兴趣和主动积极的思维活动及具体情境中对变量等概念的反馈和理解。
附板书设计: 小车下滑的时间 1.①支撑物h越高,小车下滑时间t越短; ②随着时间x的增加,我国人口总数y增加. 其中h和t,x和y都是变量.①中h是自变量,t是因变量;②中x是自变量,y是因变量. 2.借助表格,可以表示因变量随自变量的变化而变化的情况.
教后反思:
题组练习:
A 、某河受暴雨袭击,某天此河水的水位记录为下表:
时间/小时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
依据此表回答下列问题:
(1)上表反映了哪两个变量之间的关系?
(2)12时,水位是多少?
(3)哪一时段水位上升最快?
B、(p165)研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量(千克/公顷) 0 34 67 101 135 202 259 336 404 471
土豆产量 (吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75
依据此表回答下列问题:
(1)此表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说一说你的理由。
(4)粗略说一说氮肥的施用量对土豆产量的影响。
C、某婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,5周岁、10周岁时的体重分别大约是1周岁时的2倍、3倍。
上述哪两个量在变化?自变量和因变量各是什么?
某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
年龄 刚出生 6个月 1周岁 2周岁 5周岁 10周岁
体重/千克
(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的。
目标检测:
训练平台
一个专卖香蕉的水果小贩,每千克香蕉卖3、5元,某日他忘了带计算器,给算账带来不便,于是他通过笔算在硬纸板上作了一个表格,使他在算账时只需作简单的加法就可以了,表格如下:
重量/千克 0、05 0、1 0、15 0、2 0、25 0、3 0、35 0、4 0、45 0、5
价格/元 0、18 0、35 0、53 0、7 0、88 1、05 1、23 1、4 1、58 1、75
当买香蕉0、5千克时,价格是多少?
如果用x表示质量,y表示价格,那么x随着的变化,y的变化趋势时什么?
请你估计当x=3千克时,y的值是多少?
爷爷告诉小强:“距离地面越高,温度越低”,并给小强出示了下面的表格:
距离地面高度/千米 0 1 2 3 4 5
温度/摄氏度 20 14 8 2 —4 —10
根据上表,爷爷还给小强出了下面几个问题,请你和小强一起来回答。
上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎样变化的?
你知道距离地面5千米的高空温度是多少?
你能猜出距离地面6千米的高空温度是多少?
提高训练
你知道地球上的人口数量是怎样变化的吗?请看下表:
时间/年 1600 1830 1930 1960 1974 1987 1999
人口数量/亿 5 10 20 30 40 50 60
现在你清楚了吧,根据上表,请回答下列问题:
上表的哪些量在发生变化?自变量和因变量各是什么?
如果用x表示时间,y表示地球上人口总数,那么随着x的变化,y的变化趋势是什么?
从1930年起,时间向后推移30年,世界人口数量变化了吗?变化了多少?
探索发现
杨嫂再就业中心的扶持下,创办了“润物”报刊零售点,对经营的某种晚报,杨嫂提供了如下信息:(1)买进一份0、02元,卖出一份0、30元;(2)一个月内(以30天计),有20天每天可以卖出200份,其余10天每天只能卖出120份;(3)一个月内,每天从报社买进的报纸份数必须相同。当天卖不掉的报纸,以每份0、10元退给报社。
一个月内每天买进该种晚报的份数分别为100份和150份时,月利润(单位:元)是多少?
上述的哪些量在发生变化?自变量和因变量各是多少/
设每天从报社买进该种晚报x份(120≤x≤200),月利润为元,请写出y与x的关系式,并确定月利润的最大值
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
