四川省德阳市第五中学2022-2023学年高二上学期开学考试数学(理)试卷(含解析)
文档属性
| 名称 | 四川省德阳市第五中学2022-2023学年高二上学期开学考试数学(理)试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 854.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 21:13:06 | ||
图片预览


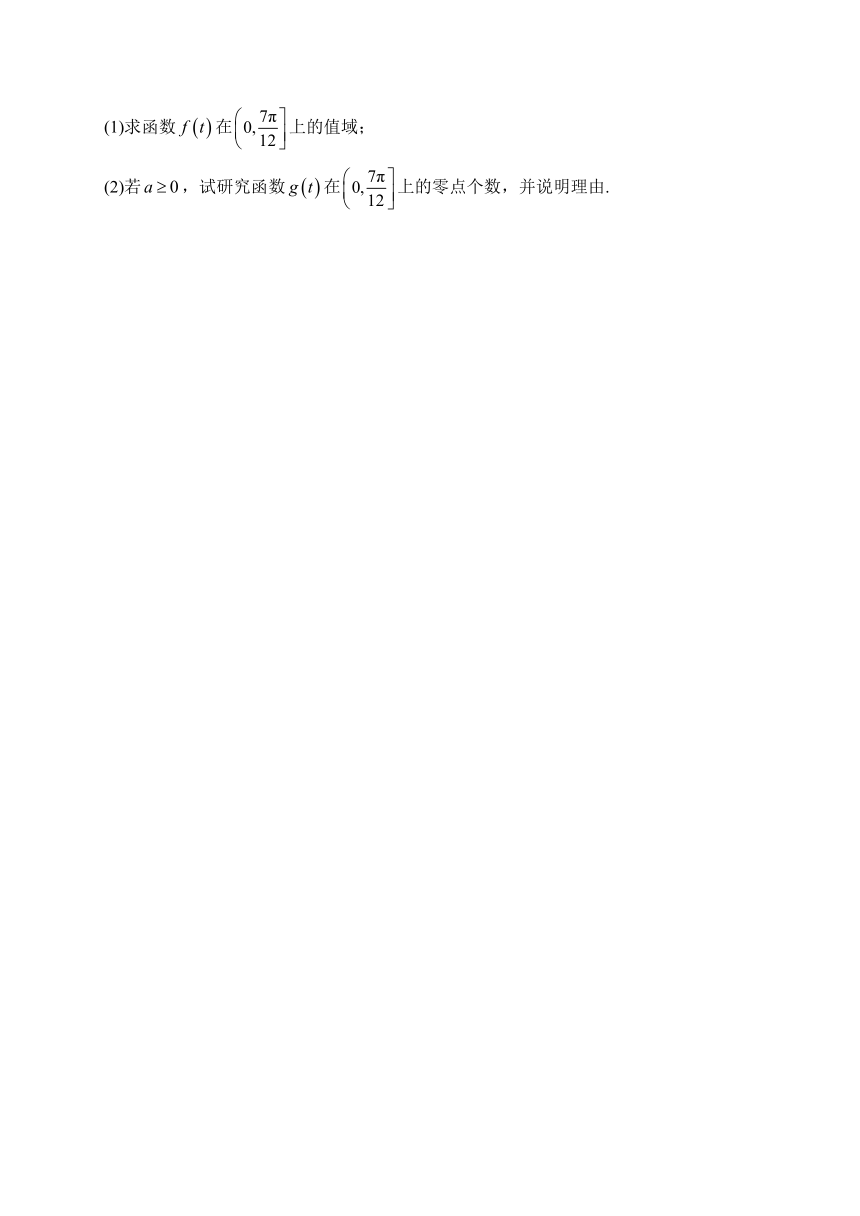

文档简介
四川省德阳市第五中学2022-2023学年高二上学期开学考试数学(理)试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、直线的倾斜角为( )
A. B. C. D.
2、已知,则的值为( )
A. B. C. D.
3、不等式的解集为( )
A. B.
C. D.
4、若非零实数a,b满足,则下列不等式一定成立的是( )
A. B. C. D.
5、下列函数中最小值为4的是( )
A. B.
C. D.
6、已知直线,.若,则实数( )
A.-1或1 B.0或1 C.-1或2 D.-3或2
7、若实数x,y满足约束条件,则的最小值是( )
A. B. C. D.
8、已知在递减等比数列中,,,若,则( )
A.6 B.7 C.8 D.9
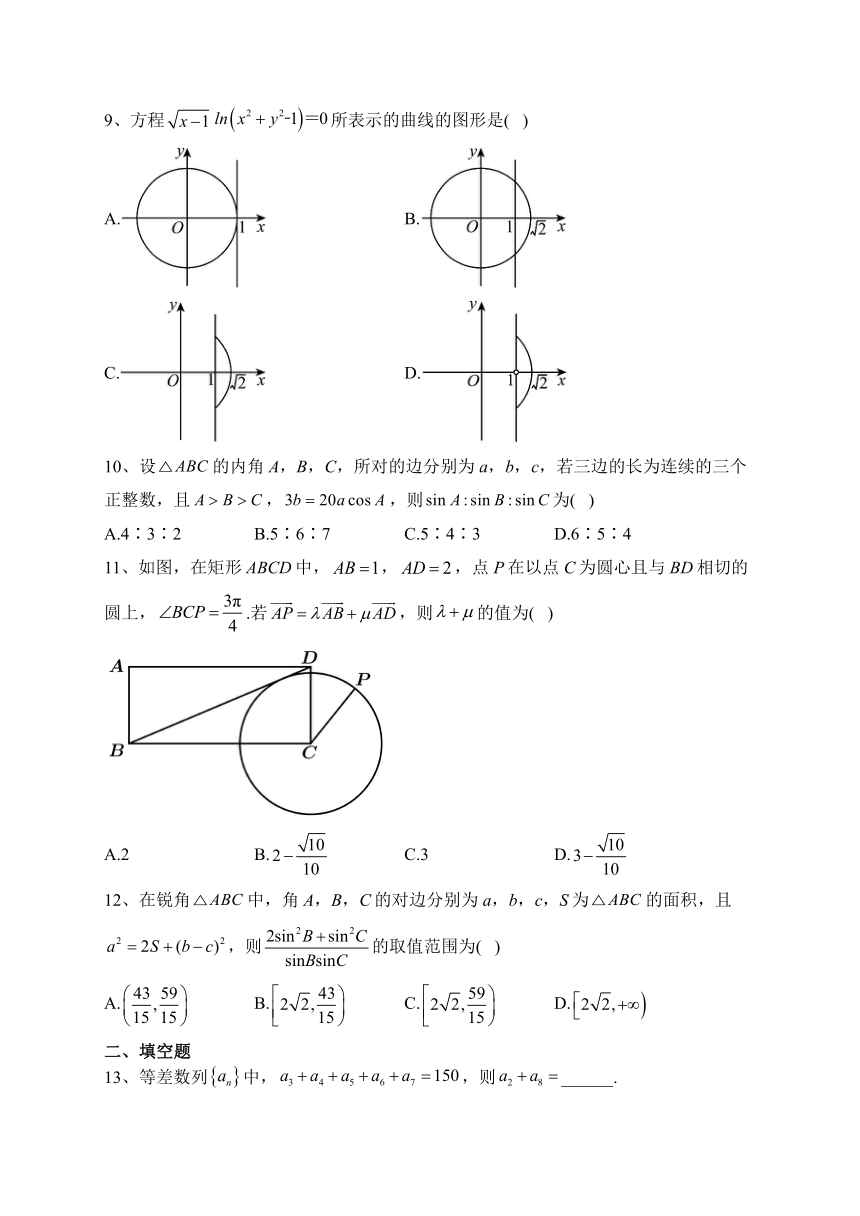
9、方程所表示的曲线的图形是( )
A. B.
C. D.
10、设的内角A,B,C,所对的边分别为a,b,c,若三边的长为连续的三个正整数,且,,则为( )
A.4∶3∶2 B.5∶6∶7 C.5∶4∶3 D.6∶5∶4
11、如图,在矩形ABCD中,,,点P在以点C为圆心且与BD相切的圆上,.若,则的值为( )
A.2 B. C.3 D.
12、在锐角中,角A,B,C的对边分别为a,b,c,S为的面积,且,则的取值范围为( )
A. B. C. D.
二、填空题
13、等差数列中,,则______.
14、已知是边长为2的正三角形,D是AC的中点,则______.
三、解答题
15、若直线与曲线有公共点,则b的取值范围是______.
16、已知中,点D在边AC上,,则的取值范围为______.
17、已知向量,,与垂直.
(1)求的值;
(2)求向量与夹角的余弦值.
18、已知的三个顶点坐标为,,.
(1)求BC的中线所在直线方程的一般式方程;
(2)求的面积.
19、设函数.
(1)求的周期和最值;
(2)已知a,b,c分别是内角A,B,C的对边,,,,,求线段CD的长.
20、已知数列的前n项和为,,且.
(1)求的通项公式;
(2)设,求数列的前n项和.
21、已知以点为圆心的圆与直线相切,过点的直线l与圆A相交于M,N两点,Q是MN的中点,.
(1)求圆A的标准方程;
(2)求直线l的方程.
22、数学家研究发现,音叉发出的声音(音叉附近空气分子的振动)可以用数学模型来刻画.1807年,法国数学家傅里叶用一个纯粹的数学定理表述了任何周期性声音的公式是形如的简单正弦函数之和.若某种声音的模型是函数,,.
(1)求函数在上的值域;
(2)若,试研究函数在上的零点个数,并说明理由.
参考答案
1、答案:D
解析:直线的斜率为,所以倾斜角.
故选:D.
2、答案:A
解析:平方得:,即,解得:
故选:A
3、答案:D
解析:由题意得,等价于,即,所以解集为.故选:D
4、答案:D
解析:对于A中,由,因为,可得,因为ab不确定,所以A错误;
对于B中,只有当,,a,b不相等时,才有成立,所以B错误;
对于C中,例如,,此时满足,但,所以C错误;
对于D中,由不等式的基本性质,当时,可得成立,所以D正确.
故选:D
5、答案:C
解析:对于A,,当且仅当时取等号,所以其最小值为3,A不符合题意;
对于B,因为,,当且仅当时取等号,等号取不到,所以其最小值不为4,B不符合题意;
对于C,因为函数定义域为R,而,,当且仅当,即时取等号,所以其最小值为4,C符合题意;
对于D,,函数定义域为,而且,如当,,D不符合题意.故选:C.
6、答案:C
解析:若,则,解得或.故选:C.
7、答案:B
解析:画出满足约束条件的可行域,
如下图所示:
目标函数化为,
由,解得,设,
当直线过A点时,
取得最小值为.故选:B.
8、答案:A
解析:在递减等比数列中,①,②,,,
设等比数列的公比为q,
则,解得,,
故选:A.
9、答案:D
解析:因为方程
所以可得或,
即或,且
所以曲线为直线与圆在直线的右边部分构成,
故选D.
10、答案:D
解析:因为a,b,c为连续的三个正整数,且,可得,,①又因为,由余弦定理可知,则
,②
联立①②,化简可得,解得或(舍去),则,,
又由正弦定理可得,.故选D.
11、答案:B
解析:设圆C的半径为,则,
以点C为坐标原点,BC、CD所在直线分别为x、y轴建立如下图所示的平面直角坐标系,
则、、、,
,,,
由,得,
所以,,解得,因此,.
故选:B.
12、答案:C
解析:由三角形面积公式可得:,故,
,故,
因为,所以,
解得:或0,
因为为锐角三角形,所以舍去,
故,,
由正弦定理得:
,
其中,
因为为锐角三角形
所以,故,所以,,
,,
令,则为对勾函数,在上单调递减,在上单调递增,
则,
又,,
因为,所以,
则.
故选:C
13、答案:60
解析:由题意知,,
则由等差数列的性质得,,即,
所以,
故答案为:60.
14、答案:-3
解析:由题意得,为,,所以
15、答案:
解析:由,解得
根据二次函数的性质得出,即
曲线可化为,
所以该曲线表示圆心为,半径为2的半圆
因为直线与曲线有公共点,所以它位于,之间,如下图所示
当直线运动到时,过,代入得:
当直线运动到时,此时与曲线相切
则,解得或(舍)
要使得直线与曲线有公共点,则
故答案为:
16、答案:
解析:设,,则,
设,则,
在中,由余弦定理得,
在中,由余弦定理得,
所以,
因为,,所以,则,
所以,则.
故答案为:.
17、答案:(1)
(2)
解析:(1)因为,且与垂直,
所以,即,即,解得.
(2)
,
,
设向量与的夹角为,所以.
18、答案:(1);
(2)
解析:(1)设BC的中点,则,即.
,
所以BC的中线所在直线方程为,即.
(2),,
所以,即.
,,
所以.
19、答案:(1),,
(2)
解析:(1)
可得的周期,
可得,;
(2)因为,
所以,
因为,,
所以可得
又,,
所以由余弦定理,可得,整理可得,解得,或-2(舍去),
又,
所以,
在中,由余弦定理可得
20、答案:(1)
(2)
解析:(1)因为①,
所以②,
②-①得即,
所以,
又当时,,又,所以,所以,
所以,所以数列是以1为首项,2为公比的等比数列,
所以.
(2)由(1)可得,
所以,
则
两式相减得,
所以.
21、答案:(1)
(2)或
解析:(1)设圆A半径为R,由圆与直线相切得,
所以圆A的标准方程为.
(2)当直线l与x轴垂直时,即,此时,符合题意;
当直线l不与x轴垂直时,设方程为,即,
Q是MN的中点,,所以,即,解得,所以直线l为:.
所以直线l的方程为或.
22、答案:(1)
(2)当或时,在上只有一个零点;
当时,在上有两个零点;
当时,在上有三个零点
解析:(1)因为,所以,
所以,即,
所以函数在上的值域为.
(2)因为,所以.
①当时,,因为,所以,解得,
所以上只有一个零点.
②当时,或.
令,,则
(ⅰ)若,记则在上单调递减,且,,
所以,由①得,所以在上只有一个零点.
(ⅱ)若,则在上单调递减,在上单调递增,且,,
所以,由①得;,因为,所以,解得;
所以在上有两个零点.
(ⅲ)若,则在上单调递减,在上单调递增,且,,
,由①得;,当时,令,,
则,,
根据零点存在定理,所以连续函数在上存在零点,
因为在上单调递减,所以连续函数在上只有一个零点.
同理,连续函数在上只有一个零点.
所以在上有三个零点.
综上,当或时,在上只有一个零点;
当时,在上有两个零点;
当时,在上有三个零点.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、直线的倾斜角为( )
A. B. C. D.
2、已知,则的值为( )
A. B. C. D.
3、不等式的解集为( )
A. B.
C. D.
4、若非零实数a,b满足,则下列不等式一定成立的是( )
A. B. C. D.
5、下列函数中最小值为4的是( )
A. B.
C. D.
6、已知直线,.若,则实数( )
A.-1或1 B.0或1 C.-1或2 D.-3或2
7、若实数x,y满足约束条件,则的最小值是( )
A. B. C. D.
8、已知在递减等比数列中,,,若,则( )
A.6 B.7 C.8 D.9
9、方程所表示的曲线的图形是( )
A. B.
C. D.
10、设的内角A,B,C,所对的边分别为a,b,c,若三边的长为连续的三个正整数,且,,则为( )
A.4∶3∶2 B.5∶6∶7 C.5∶4∶3 D.6∶5∶4
11、如图,在矩形ABCD中,,,点P在以点C为圆心且与BD相切的圆上,.若,则的值为( )
A.2 B. C.3 D.
12、在锐角中,角A,B,C的对边分别为a,b,c,S为的面积,且,则的取值范围为( )
A. B. C. D.
二、填空题
13、等差数列中,,则______.
14、已知是边长为2的正三角形,D是AC的中点,则______.
三、解答题
15、若直线与曲线有公共点,则b的取值范围是______.
16、已知中,点D在边AC上,,则的取值范围为______.
17、已知向量,,与垂直.
(1)求的值;
(2)求向量与夹角的余弦值.
18、已知的三个顶点坐标为,,.
(1)求BC的中线所在直线方程的一般式方程;
(2)求的面积.
19、设函数.
(1)求的周期和最值;
(2)已知a,b,c分别是内角A,B,C的对边,,,,,求线段CD的长.
20、已知数列的前n项和为,,且.
(1)求的通项公式;
(2)设,求数列的前n项和.
21、已知以点为圆心的圆与直线相切,过点的直线l与圆A相交于M,N两点,Q是MN的中点,.
(1)求圆A的标准方程;
(2)求直线l的方程.
22、数学家研究发现,音叉发出的声音(音叉附近空气分子的振动)可以用数学模型来刻画.1807年,法国数学家傅里叶用一个纯粹的数学定理表述了任何周期性声音的公式是形如的简单正弦函数之和.若某种声音的模型是函数,,.
(1)求函数在上的值域;
(2)若,试研究函数在上的零点个数,并说明理由.
参考答案
1、答案:D
解析:直线的斜率为,所以倾斜角.
故选:D.
2、答案:A
解析:平方得:,即,解得:
故选:A
3、答案:D
解析:由题意得,等价于,即,所以解集为.故选:D
4、答案:D
解析:对于A中,由,因为,可得,因为ab不确定,所以A错误;
对于B中,只有当,,a,b不相等时,才有成立,所以B错误;
对于C中,例如,,此时满足,但,所以C错误;
对于D中,由不等式的基本性质,当时,可得成立,所以D正确.
故选:D
5、答案:C
解析:对于A,,当且仅当时取等号,所以其最小值为3,A不符合题意;
对于B,因为,,当且仅当时取等号,等号取不到,所以其最小值不为4,B不符合题意;
对于C,因为函数定义域为R,而,,当且仅当,即时取等号,所以其最小值为4,C符合题意;
对于D,,函数定义域为,而且,如当,,D不符合题意.故选:C.
6、答案:C
解析:若,则,解得或.故选:C.
7、答案:B
解析:画出满足约束条件的可行域,
如下图所示:
目标函数化为,
由,解得,设,
当直线过A点时,
取得最小值为.故选:B.
8、答案:A
解析:在递减等比数列中,①,②,,,
设等比数列的公比为q,
则,解得,,
故选:A.
9、答案:D
解析:因为方程
所以可得或,
即或,且
所以曲线为直线与圆在直线的右边部分构成,
故选D.
10、答案:D
解析:因为a,b,c为连续的三个正整数,且,可得,,①又因为,由余弦定理可知,则
,②
联立①②,化简可得,解得或(舍去),则,,
又由正弦定理可得,.故选D.
11、答案:B
解析:设圆C的半径为,则,
以点C为坐标原点,BC、CD所在直线分别为x、y轴建立如下图所示的平面直角坐标系,
则、、、,
,,,
由,得,
所以,,解得,因此,.
故选:B.
12、答案:C
解析:由三角形面积公式可得:,故,
,故,
因为,所以,
解得:或0,
因为为锐角三角形,所以舍去,
故,,
由正弦定理得:
,
其中,
因为为锐角三角形
所以,故,所以,,
,,
令,则为对勾函数,在上单调递减,在上单调递增,
则,
又,,
因为,所以,
则.
故选:C
13、答案:60
解析:由题意知,,
则由等差数列的性质得,,即,
所以,
故答案为:60.
14、答案:-3
解析:由题意得,为,,所以
15、答案:
解析:由,解得
根据二次函数的性质得出,即
曲线可化为,
所以该曲线表示圆心为,半径为2的半圆
因为直线与曲线有公共点,所以它位于,之间,如下图所示
当直线运动到时,过,代入得:
当直线运动到时,此时与曲线相切
则,解得或(舍)
要使得直线与曲线有公共点,则
故答案为:
16、答案:
解析:设,,则,
设,则,
在中,由余弦定理得,
在中,由余弦定理得,
所以,
因为,,所以,则,
所以,则.
故答案为:.
17、答案:(1)
(2)
解析:(1)因为,且与垂直,
所以,即,即,解得.
(2)
,
,
设向量与的夹角为,所以.
18、答案:(1);
(2)
解析:(1)设BC的中点,则,即.
,
所以BC的中线所在直线方程为,即.
(2),,
所以,即.
,,
所以.
19、答案:(1),,
(2)
解析:(1)
可得的周期,
可得,;
(2)因为,
所以,
因为,,
所以可得
又,,
所以由余弦定理,可得,整理可得,解得,或-2(舍去),
又,
所以,
在中,由余弦定理可得
20、答案:(1)
(2)
解析:(1)因为①,
所以②,
②-①得即,
所以,
又当时,,又,所以,所以,
所以,所以数列是以1为首项,2为公比的等比数列,
所以.
(2)由(1)可得,
所以,
则
两式相减得,
所以.
21、答案:(1)
(2)或
解析:(1)设圆A半径为R,由圆与直线相切得,
所以圆A的标准方程为.
(2)当直线l与x轴垂直时,即,此时,符合题意;
当直线l不与x轴垂直时,设方程为,即,
Q是MN的中点,,所以,即,解得,所以直线l为:.
所以直线l的方程为或.
22、答案:(1)
(2)当或时,在上只有一个零点;
当时,在上有两个零点;
当时,在上有三个零点
解析:(1)因为,所以,
所以,即,
所以函数在上的值域为.
(2)因为,所以.
①当时,,因为,所以,解得,
所以上只有一个零点.
②当时,或.
令,,则
(ⅰ)若,记则在上单调递减,且,,
所以,由①得,所以在上只有一个零点.
(ⅱ)若,则在上单调递减,在上单调递增,且,,
所以,由①得;,因为,所以,解得;
所以在上有两个零点.
(ⅲ)若,则在上单调递减,在上单调递增,且,,
,由①得;,当时,令,,
则,,
根据零点存在定理,所以连续函数在上存在零点,
因为在上单调递减,所以连续函数在上只有一个零点.
同理,连续函数在上只有一个零点.
所以在上有三个零点.
综上,当或时,在上只有一个零点;
当时,在上有两个零点;
当时,在上有三个零点.
同课章节目录
