《初中同步测控全优设计》2013-2014学年人教版七年级数学上册例题与讲解:第一章1.2 有理数
文档属性
| 名称 | 《初中同步测控全优设计》2013-2014学年人教版七年级数学上册例题与讲解:第一章1.2 有理数 |
|
|
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-06 00:00:00 | ||
图片预览



文档简介
1.2 有理数
1.有理数
(1)定义:整数和分数统称为有理数.
(2)分类:①按定义分类:
有理数
②按性质分类(正负性):
有理数
(3)理解:①分类标准不同,分类结果也不 ( http: / / www.21cnjy.com )一样;②有理数的另一个概念:形如(m,n为整数,且n≠0)的数是有理数,整数可以看作是分母为1的数,小数(有限或无限循环)都可以化为分数,所以所有的有理数都可以写成分数的形式.
(4)集合:所有的正数在一起组成正数集合,所有的负数在一起组成负数集合,0既不属于正数集合也不属于负数集合.
破疑点 有理数的理解 ①因为有限小数和无 ( http: / / www.21cnjy.com )限循环小数都可以化为分数,所以有限小数和无限循环小数都是分数;②按以上两种有理数的分类方式,我们一般不把整数看作是分母为1的分数.把整数和分数看作是不同类的数;③π不是有理数,它是无限不循环小数,它可以取近似值为3.14,但它不同于3.14.
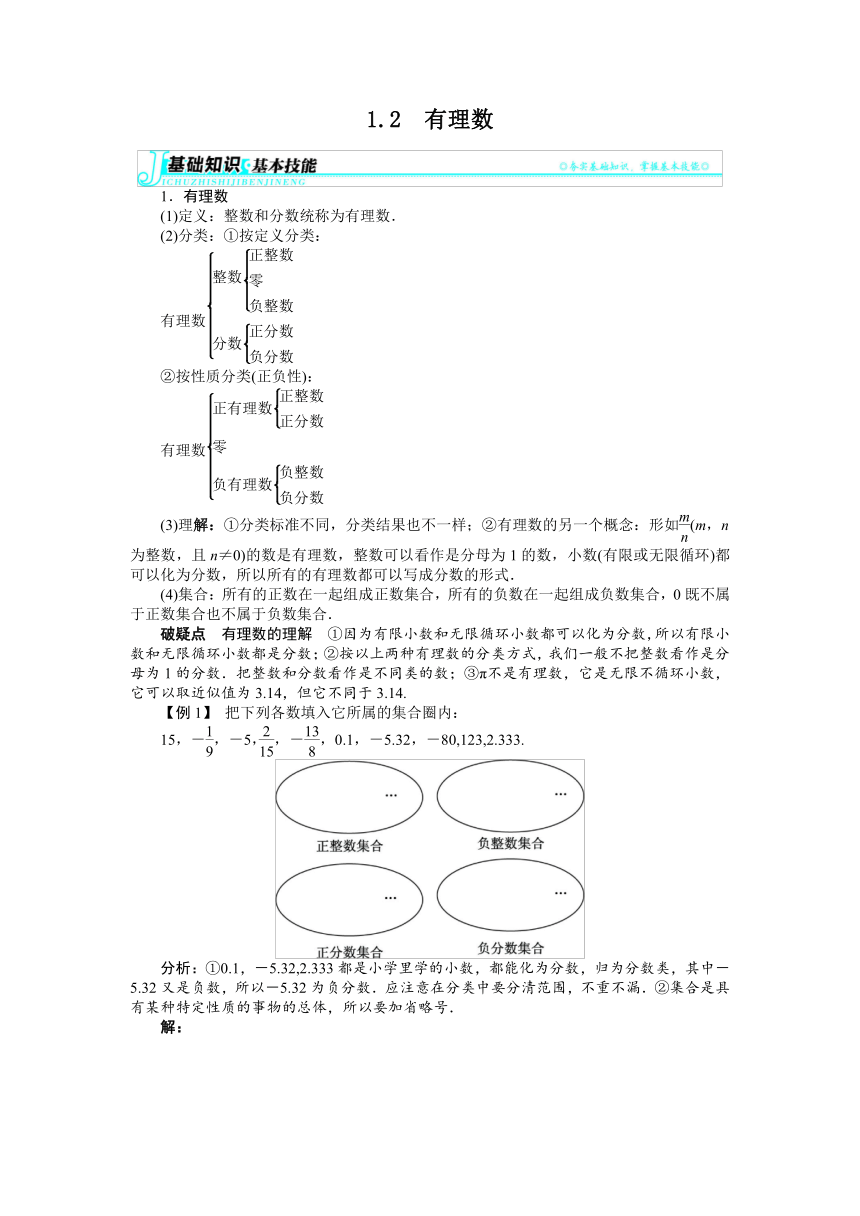
【例1】 把下列各数填入它所属的集合圈内:
15,-,-5,,-,0.1,-5.32,-80,123,2.333.
分析:①0.1,-5.32,2.333都是 ( http: / / www.21cnjy.com )小学里学的小数,都能化为分数,归为分数类,其中-5.32又是负数,所以-5.32为负分数.应注意在分类中要分清范围,不重不漏.②集合是具有某种特定性质的事物的总体,所以要加省略号.
解:
2.数轴的概念及画法
(1)概念:一般地,在数学中人们用画图的方式把数“直观化”,通常用一条直线上的点表示数,这条直线叫做数轴.
(2)三要素:原点、正方向和单位长度,三者缺一不可.
①原点:在直线上任取一个点表示数0,这个点叫做原点;
②正方向:规定直线上从原点向右(或向上)的方向为正方向,从原点向左(或向下)的方向为负方向;
③单位长度:选取适当的长度 ( http: / / www.21cnjy.com )为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…,原点向左,每隔一个单位长度取一个点,依次表示-1,-2,-3,….
(3)数轴的概念包含的意思:
①数轴是一条直线,可以向两端无限延伸;
②原点的位置、单位长度大小的确定都是根据实际而定的.一般取向右的方向为正方向.
③原点是数轴的“基准点”.
(4)数轴的画法:
要正确迅速地画出数轴,可按以下步骤进行:
①“画”就是先画一条水平的直线;
②“取”就是在直线上选取一点表示原点(原点表示的数是0);
③“选”就是选择向右的方向为正方向(用 ( http: / / www.21cnjy.com )箭头表示),那么相反的方向,即从原点向左为负方向,然后选取适当的长度作为单位长度,用细短线在直线上画出;
④“标”就是从原点向右,依次标出1,2,3,…;从原点向左,依次标出-1,-2,-3,….
画数轴的步骤可简单归纳为“一画、二取、三选、四标”.
解技巧 数轴的画法 画数轴时根据实际问题的需要可选取不同的数作为单位长度,同一数轴上的单位长度必须一致.
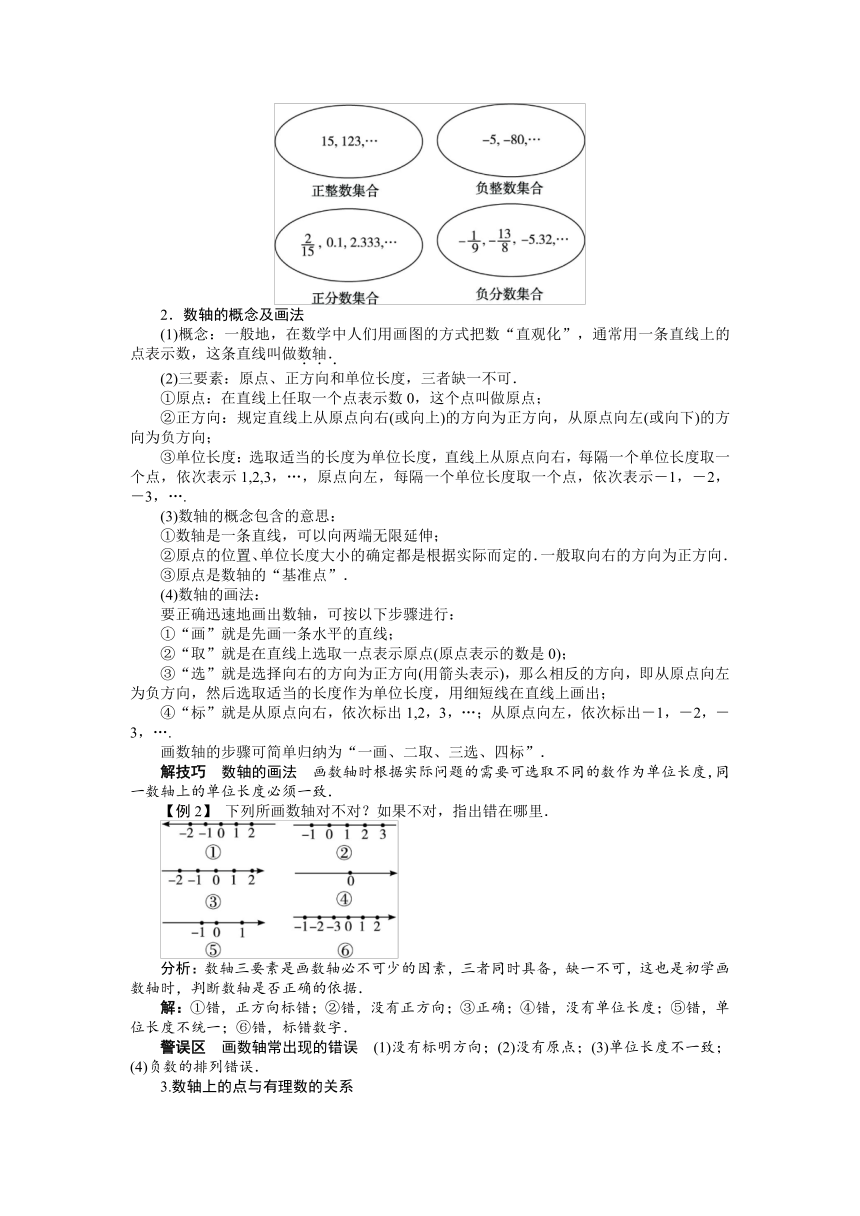
【例2】 下列所画数轴对不对?如果不对,指出错在哪里.
分析:数轴三要素是画数轴必不可少的因素,三者同时具备,缺一不可,这也是初学画数轴时,判断数轴是否正确的依据.
解:①错,正方向标错;②错,没有正方向;③正确;④错,没有单位长度;⑤错,单位长度不统一;⑥错,标错数字.
警误区 画数轴常出现的错误 (1)没有标明方向;(2)没有原点;(3)单位长度不一致;(4)负数的排列错误.
3.数轴上的点与有理数的关系
(1)数对应点:每一个有理数都可以用数轴上的点表示出来,整数可以直接找到对应的整数点,分数可以分成多少份(分母的份数),取其中的分子数份.
(2)点表示数:数轴上的每一个点都表示一个数(不仅仅是有理数).
(3)一一对应:每个点都表示唯一的一个数,每个数都有唯一的对应点.
(4)理解:①借助于数轴把数直观的排列在一条直线上,便于归类、比较.
②若设a为一个正数,则数轴上表示数a的点在原点的右边,与原点的距离是a个单位长度,表示-a的点在原点的左边,与原点的距离是a个单位长度.
谈重点 数轴上的点与有理数的关系 ( http: / / www.21cnjy.com ) 正数用原点右边的点表示,反过来原点右边的点都表示正数;负数用原点左边的点表示,反过来原点左边的点都表示负数;0用原点表示,原点表示0.
【例3】 下列语句:①数轴上的点仅 ( http: / / www.21cnjy.com )能表示整数;②数轴是一条直线;③数轴上的一个点只能表示一个数;④数轴上找不到既不表示正数,又不表示负数的点;⑤数轴上的点所表示的数都是有理数.正确的说法有( ).
A.1个 B.2个
C.3个 D.4个
解析:结合数轴上的点与有理数的特点,①是错误 ( http: / / www.21cnjy.com )的;④中可以含有0,⑤中应该是所有的有理数都可以在数轴上找出对应的点,但数轴上的点并不都表示有理数,以后学习的无理数也可以用数轴上的点表示.所以④、⑤也错误,只有②、③是正确的,故选B.
答案:B
所有有理数都可以在数轴上找到座位,但每个座位表示的数不一定是有理数.
4.相反数
(1)定义:只有符号不同的两个数叫做互为相反数.特别地,0的相反数是0.
(2)对称性:两个互为相反数的数,在数轴上的对应点(0除外),都在原点两旁,是距离原点相等的两个点.即:互为相反数的两个数在数轴上的对应点关于原点对称,这两点到原点的距离相等.
解技巧 相反数的求法 ① ( http: / / www.21cnjy.com )在正数前面添上一个“-”号,就得到这个正数的相反数,是一个负数;把负数前的“-”号去掉,就得到这个负数的相反数,是一个正数;②我们把a的相反数记为-a.a表示任意一个数,可以是正数、负数和0.
【例4】 3的相反数是_ ( http: / / www.21cnjy.com )_________,-5.8是______的相反数,a的相反数是______,a-b的相反数是______,0的相反数是______.
解析:只有符号不同的两个数互为相反数,所以只改变符号即可,其中a-b是一个数,是个整体,所以要加括号.
答案:-3 5.8 -a -(a-b) 0
5.运用相反数化简符号
(1)理解:在任意一个数前面添上“-”号,新的数就是原数的相反数.
如:+5的相反数表示为-(+5),而5 ( http: / / www.21cnjy.com )的相反数就是-5,所以-(+5)=-5;-5的相反数表示为-(-5),我们知道-5的相反数是5,所以-(-5)=5,因此运用相反数可以进行符号化简:-(-10)=10,-(+6)=-6等;
(2)分类:简单的符号化简共有3种情况:
①-(+a)=-a;②+(-a)=-a;③-(-a)=a.
(3)延伸:①-[-(-a)]=-a;-[+(-a)]=a等.②-0=0,表示0的相反数是0.
【例5】 化简下列各符号:
(1)-[-(-2)];
(2)+{-[-(+5)]};
(3)-{-{-…-(-6)}…}(共n个负号).
解析:化简的法则是:结果的符号与负号的个数有关,有偶数个负号时,结果为正;有奇数个负号时,结果为负.
答案:(1)-2;(2)5;(3)当n为偶数时,为6;当n为奇数时,为-6.
6.绝对值
(1)定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值.
(2)表示:数a的绝对值表示为|a|.
(3)求法:①一个正数的绝对值是它本身;
②一个负数的绝对值是它的相反数;
③0的绝对值是0.
用字母表示为:如果a>0,那么|a|=a;如果a=0,那么|a|=0;如果a<0,那么|a|=-a.
归纳为|a|=
谈重点 绝对值的理解 ①确定一个非零 ( http: / / www.21cnjy.com )数的绝对值首先应看这个数是正数还是负数,是正数则是它本身,是负数则是它的相反数,特别是字母表示的数更应先确定正负,再去绝对值号;②由定义可知,任何数的绝对值都是非负数,所以不存在绝对值是负数的数;③绝对值是一个正数的数有两个,它们互为相反数.
【例6】 绝对值为4的数是( ).
A.±4 B.4
C.-4 D.2
解析:绝对值是4的数有两个,+4和-4.
不要弄错哦,绝对值为一个正数的数有两个,它们互为相反数.
答案:A
7.数的大小的比较
(1)借助数轴比较数的大小:数轴上的点表示的数从左往右逐渐增大,并且右边的数总比左边的数大.
(2)正数、0、负数大小的比较:
正数大于0,0大于负数,正数大于负数.
(3)用绝对值比较两个负数的大小:
两个负数相比较,绝对值大的反而小.
解技巧 数的大小比较方法选择 数 ( http: / / www.21cnjy.com )的比较一般有四种情况:①正数、负数、0的比较,直接按法则;②正数之间的比较,符合小学认知,大就是大;③两个负数大小的比较,一是比较绝对值的大小,绝对值大的反而小,二是表示在数轴上比较大小,右边的数总比左边的大;④不是最简数,化为最简后再比较大小.
【例7】 用“>”“=”“<”填空:
①-7______-5;②-0.1______-0.01;
③______-;④0__________-3.14;
⑤______0.25;
⑥-|-3.2|______-(-3.2).
解析:③、④为正数、负数、0的大小比较, ( http: / / www.21cnjy.com )很显然③>-,④0>-3.14;①、②为两负数大小的比较,根据绝对值大的反而小知:①-7<-5;②-0.1<-0.01;⑤是两正数的比较,=0.25;⑥需要化简后比较,-|-3.2|=-3.2,-(-3.2)=3.2,所以-|-3.2|<-(-3.2).
答案:< < > > = <
谈重点 比较大小 异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
8.有理数分类的应用延伸
(1)按照不同的分类方法,数可以分为不同的类,但是无论按哪种方法分类,都必须全面、严密,不重不漏;
(2)类似于某同学是某学校、某年级、 ( http: / / www.21cnjy.com )某班的学生一样,数的范围也有大小,比如:-8是有理数中的整数类,又是整数中的负整数,所以每个数既是大类别中的数,又归为不同的子类别;③目前所学数中π不是有理数.
破疑点 0的理解 ①0既不是正数也不 ( http: / / www.21cnjy.com )是负数,它是有理数,是整数,也是自然数;②0和正整数统称为自然数,没有负自然数;③整数和分数中有正整数、0、负整数、正分数、负分数之分.
【例8】 在下表适当的空格里画上“√”号.
有理数 整数 分数 正整数 负分数 自然数
-9是
-2.35是
0是
+5是
分析:正是由于数的范围大小不同 ( http: / / www.21cnjy.com ),所以数归为不同的类.如:-9是有理数,也是整数、是整数中的负整数,-2.35是有理数,也是分数,是分数中的负分数.
解:
有理数 整数 分数 正整数 负分数 自然数
-9是 √ √
-2.35是 √ √ √
0是 √ √ √
+5是 √ √ √ √
9.绝对值的化简和计算
化简绝对值符号主要根据绝对值的非负性,解题时看清楚“-”号在绝对值符号的里面还是外面.如果“-”号在绝对值符号的里面,化简时把“-”号去掉;如果“-”号在绝对值符号的外面,化简时不能把“-”号去掉.
解技巧 去绝对值的关键 化简绝对值符号的关键是判断绝对值符号内的数是正数还是负数.
【例9】 化简(1)-;(2)+|-24|;
(3);(4)|-(-7.5)|.
分析:先判断数的符号,再求绝对值.
解:(1)-=-;
(2)+|-24|=24;
(3)=3;
(4)|-(-7.5)|=7.5.
10.数轴上两点间的距离与点表示的数之间的关系
(1)数轴使数和直线上的点建立了对应关系,它揭示了数和形的内在联系;正是这种联系,使得数轴上两点之间的距离与所表示的数之间存在密切关系.
(2)数轴上表示数a的点与原点之间的距 ( http: / / www.21cnjy.com )离:当a为一个正数时,它与原点的距离是a个单位长度,当a是负数时,它与原点的距离是|a|个单位长度;当a是0时,距离为0;
(3)注意:到某一点距离等于a(a是正数)的点有两个,在点的左右两侧各一个.
解技巧 数形结合求距离 解决此类问题的最好方法是画出数轴,并表示出所求的数,再求两点间的距离.
【例10-1】 在数轴上,表示-2的点与原点的距离是__________;表示的点与原点的距离是__________.
解析:-2在原点的左侧,到原点的距离是2个单位长度,到原点的距离是个单位长度.
答案:2
【例10-2】 数轴上点A到原点0的距离等于6,点B到原点0的距离等于4,则A,B两点之间的最大距离是__________.
解析:如图,
在数轴上,A点到原点的距离是6,所以A点可 ( http: / / www.21cnjy.com )以是-6,6表示的点,即图中的A1,A2点,B点是-4,4表示的点,即B1,B2点,A,B两点之间的最大距离就是A1B2或A2B1的长度,它们相等,都是6+4=10,所以A,B两点之间的最大距离是10个单位长度.
答案:10
11.字母表示的数的绝对值的求法应用
因为用字母所表示的数既可以是 ( http: / / www.21cnjy.com )正数也可以是负数,还可以是0,它具有不确定性,而求绝对值首先要考虑的就是符号,因此求字母表示的数的绝对值时,必须考虑题目中给定的条件,若有限定条件,就按限定条件求出,若没有限定条件,则要分正、负、0三种情况讨论.
解技巧 绝对值的求法 ①限制型逆用求 ( http: / / www.21cnjy.com )法,如:|a|=6,那么a=±6;②开放型分类讨论求法:如求|x|+x的值,当x>0时,|x|=x,所以|x|+x=x+x=2x,当x<0时,|x|=-x,原式=0,当x=0时,原式=0.③化简型求法:如:|a|=|-8|,|-a|=|-8|,|-a|=|8|都能化为|a|=|8|=8解决.
【例11-1】 如果|a|=5,|b|=4,a<b,那么a=__________,b=__________.
解析:因为±5的绝对值都是5,所以a= ( http: / / www.21cnjy.com )+5或-5,同样由|b|=4得b=±4,当a=-5时,-5<4,-5<-4,所以b=±4都能使a<b成立,而当a=5时,5>4,5>-4,所以b=±4都不能满足条件a<b,所以a=-5,b=±4.
答案:-5 ±4
【例11-2】 若|a|=|b|,则a,b的关系是( ).
A.a=b B.a=-b
C.a=b或a=-b D.a=0且b=0
解析:方法一:因为绝对值相等,所以数a,b就数字部分看(不考虑符号)应该完全相同,只是符号有正、负两种情况,组合会有4种情况,当同正或同负时,两数的符号相同,数字部分又完全一样,所以相等,即a=b,异号时,两数只有符号不同,所以两数互为相反数,即a=-b,所以两数要么相等,要么互为相反数,故选C.
方法二:此题还可以选择一些特殊的值,如a ( http: / / www.21cnjy.com )=2,3,5,…,那么相对应的b=±2,±3,±5,…,从而得到a与b的值同号时相等,异号时互为相反数,即a=b或a=-b.
答案:C
12.利用数轴解决生活中的实际问题
本节知识常与运动问题结合在一起,利用数形结合将运动问题解决.这种利用数形结合解决问题的方法是中考考查的热点题型之一.
数轴是一种数学工具,它使数和数轴上的点建立了 ( http: / / www.21cnjy.com )对应关系,揭示了数与形之间的内在联系,也为我们研究问题提供了新的方法.数轴是联系数与形的桥梁,是数形结合的具体体现,利用数轴可以解决生活中的许多问题.
运用数轴可以直观表示点的移动,正确找出数在数轴上的对应点,会由数轴上的点的位置确定对应的数,是解决这类问题的关键.
【例12】 超市、书店、玩具店依次坐 ( http: / / www.21cnjy.com )落在一条东西走向的大街上,超市在书店西边20米处,玩具店位于书店东边50米处.小明从书店出来沿街向东走了50米,接着又向东走了-80米,此时小明的位置在何处?在数轴上标出超市、书店、玩具店的位置,以及小明最后的位置.
分析:书店处于超市和玩具店之间,且书店 ( http: / / www.21cnjy.com )与玩具店之间的距离是50米,书店与超市之间的距离是20米,这样可以画出数轴,即可表示出小明最后的位置.
解决点的移动问题,可画出数轴,在数轴上表 ( http: / / www.21cnjy.com )示点的移动,关键是确定原点,最后的点相对于原点来说,若在原点的右侧,表示的是正数,若在原点的左侧,则表示的是负数.
解:根据题意可以画出如图所示的数轴,小明位于超市西边10米处.
13.利用绝对值解决实际问题
绝对值的产生来源于实际问题的需要,反过来又可以运用它解决一些实际问题,主要有以下两类:
(1)判断物体或产品的质量
用绝对值判断物体或产品偏离标准的程度,绝对值越小,越接近标准,质量就越好.
方法:①求每个数的绝对值;
②比较所求绝对值的大小;
③根据“绝对值小的越接近标准”作出判断.
(2)利用绝对值求距离
路程问题中,当出现用“+”“-”号表示带方向的路程,求最后实际路程时,实际上是求绝对值的和.
方法:
①求各个数的绝对值;
②求所有数的绝对值的和;
③写出答案.
【例13-1】 某汽车配件厂生产一 ( http: / / www.21cnjy.com )批圆形的橡胶垫,从中抽取6件进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查结果如下:
1 2 3 4 5 6
+0.5 -0.3 +0.15 -0.1 0 0.2
用绝对值的知识说明哪个零件的质量最好?
分析:质量的好坏取决于质量偏离标准质量的绝对值,即偏离橡胶垫的标准质量的绝对值越小,越接近标准,其质量就越好.
解:因为|+0.5|>|-0.3|>|0.2|>|+0.15|>|-0.1|>|0|,
所以第5个零件的质量最好.
【例13-2】 一天上午,出租车司机 ( http: / / www.21cnjy.com )小王在东西走向的中山路上运营,如果规定向东为正,向西为负,出租车的行车里程如下(单位:千米):+15,-3,+12,-11,-13,+3,-12,-18,请问小王将最后一位乘客送到目的地时,共行驶了多少千米?
解:|+15|+|-3|+|+12|+ ( http: / / www.21cnjy.com )|-11|+|-13|+|+3|+|-12|+|-18|=15+3+12+11+13+3+12+18=87(千米).
答:小王将最后一位乘客送到目的地时共行驶了87千米.
14.特殊值法的妙用
(1)作用:字母表示数是代数 ( http: / / www.21cnjy.com )的核心,用字母表示数为我们研究数学规律和方法提供了很多便利,但由于字母表示数的抽象性和不确定性,使含有字母的数的运算和大小的比较,变的复杂且不容易理解,取特殊值法为我们提供了简便的解法,也便于理解.同时也揭示出由特殊到一般的探索过程.
(2)方法技巧:①特殊值法 ( http: / / www.21cnjy.com )取特殊值时,所取的值一定要符合题目要求,在所规定的范围内;②要尽量简便,一般选取较小或较简单的数,以简化计算过程;③取适当的个数,并且按一定规律或顺序取值,以便于发现规律,正确解决问题;④赋值要全面,要考虑周全,考虑各种适合的可能,这也是特殊值法得到的结论是否正确的关键.特别要注意一些特殊数,如:0,±1等.如例142中要按大于1,等于1,小于1三种情况分类讨论取值,从而全面了解了在x为正数条件下的各种情况.
【例14-1】 若a<0,b>0,且|a|<|b|,试用“<”号连接a,b,-a,-b.
分析:常规解法要考虑各数值的正负,还要考虑 ( http: / / www.21cnjy.com )绝对值的大小,借助于数轴解决.但用特殊值法,在满足a<0,b>0,且|a|<|b|的条件下,可以取a=-2,b=5,这时,-a=2,-b=-5,由于-5<-2<2<5,所以-b<a<-a<b;同样可以再取一次别的数,当a=-6,b=7时,-a=6,-b=-7,由于-7<-6<6<7,所以-b<a<-a<b;由此可知四个数的大小关系是-b<a<-a<b.
解:-b<a<-a<b.
【例14-2】 若x是正数,试比较x与的大小.
分析:分三种情况列举取值,当x=1时,x的倒 ( http: / / www.21cnjy.com )数=1,倒数等于原数,即x=;当x=2,3,4,…时,x的倒数分别为,,,…,此时原数都大于它的倒数,即x>;当x=,,,…,或取小数0.6,0.7,…时,x的倒数分别为:2,3,,…,或,…,此时原数都小于倒数,即x<,因此以1为分界,包括1,共三种情况.
解:当x>1时,x>;当x=1时,x=;当x<1时,x<.
15.借助数轴比较数的大小的应用
对于简单的数的比较,如正数之间,正负数、0之间数的大小的比较可以直接写出,但对于较多的数,或复杂的数的比较,有时候借助数轴会更简单,更直观,也便于理解,
(1)依据:数轴上的点表示的数,右边的总比左边的大.
(2)分类:①具体的数的大小的比较,初学负数,特别是对于多个相近负数的比较,运用数轴会更准确、直观.同时能培养学生的数感.
②字母表示的数的大小的比较:根据数轴上字母表 ( http: / / www.21cnjy.com )示的数的位置,根据相反数、绝对值意义,标出所求数的位置(所求数表示的点),再根据数轴上的点所表示数的大小规律,写出所求数的大小关系.
【例15-1】 比较下列各数的大小:
-1.5,-0.5,-3.5,-5.
解:将这些数在数轴上表示出来,如图,
从数轴上可以看出-5<-3.5<-1.5<-0.5.
【例15-2】 数a,b在数轴上的位置如图所示,下面所给的四个选项中正确的是( ).
A.b>a B.|a|>|b|
C.-a<b D.-b>a
解析:因为a>0,b<0,所 ( http: / / www.21cnjy.com )以b<a,故排除A;因为表示b的点到原点的距离比表示a的点到原点的距离大,根据绝对值的定义可得|a|<|b|,故排除B;在数轴上将-a、-b的位置表示出来,如图所示,
显然有b<-a<0<a<-b,故排除C,故只有D正确.
答案:D
1.有理数
(1)定义:整数和分数统称为有理数.
(2)分类:①按定义分类:
有理数
②按性质分类(正负性):
有理数
(3)理解:①分类标准不同,分类结果也不 ( http: / / www.21cnjy.com )一样;②有理数的另一个概念:形如(m,n为整数,且n≠0)的数是有理数,整数可以看作是分母为1的数,小数(有限或无限循环)都可以化为分数,所以所有的有理数都可以写成分数的形式.
(4)集合:所有的正数在一起组成正数集合,所有的负数在一起组成负数集合,0既不属于正数集合也不属于负数集合.
破疑点 有理数的理解 ①因为有限小数和无 ( http: / / www.21cnjy.com )限循环小数都可以化为分数,所以有限小数和无限循环小数都是分数;②按以上两种有理数的分类方式,我们一般不把整数看作是分母为1的分数.把整数和分数看作是不同类的数;③π不是有理数,它是无限不循环小数,它可以取近似值为3.14,但它不同于3.14.
【例1】 把下列各数填入它所属的集合圈内:
15,-,-5,,-,0.1,-5.32,-80,123,2.333.
分析:①0.1,-5.32,2.333都是 ( http: / / www.21cnjy.com )小学里学的小数,都能化为分数,归为分数类,其中-5.32又是负数,所以-5.32为负分数.应注意在分类中要分清范围,不重不漏.②集合是具有某种特定性质的事物的总体,所以要加省略号.
解:
2.数轴的概念及画法
(1)概念:一般地,在数学中人们用画图的方式把数“直观化”,通常用一条直线上的点表示数,这条直线叫做数轴.
(2)三要素:原点、正方向和单位长度,三者缺一不可.
①原点:在直线上任取一个点表示数0,这个点叫做原点;
②正方向:规定直线上从原点向右(或向上)的方向为正方向,从原点向左(或向下)的方向为负方向;
③单位长度:选取适当的长度 ( http: / / www.21cnjy.com )为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…,原点向左,每隔一个单位长度取一个点,依次表示-1,-2,-3,….
(3)数轴的概念包含的意思:
①数轴是一条直线,可以向两端无限延伸;
②原点的位置、单位长度大小的确定都是根据实际而定的.一般取向右的方向为正方向.
③原点是数轴的“基准点”.
(4)数轴的画法:
要正确迅速地画出数轴,可按以下步骤进行:
①“画”就是先画一条水平的直线;
②“取”就是在直线上选取一点表示原点(原点表示的数是0);
③“选”就是选择向右的方向为正方向(用 ( http: / / www.21cnjy.com )箭头表示),那么相反的方向,即从原点向左为负方向,然后选取适当的长度作为单位长度,用细短线在直线上画出;
④“标”就是从原点向右,依次标出1,2,3,…;从原点向左,依次标出-1,-2,-3,….
画数轴的步骤可简单归纳为“一画、二取、三选、四标”.
解技巧 数轴的画法 画数轴时根据实际问题的需要可选取不同的数作为单位长度,同一数轴上的单位长度必须一致.
【例2】 下列所画数轴对不对?如果不对,指出错在哪里.
分析:数轴三要素是画数轴必不可少的因素,三者同时具备,缺一不可,这也是初学画数轴时,判断数轴是否正确的依据.
解:①错,正方向标错;②错,没有正方向;③正确;④错,没有单位长度;⑤错,单位长度不统一;⑥错,标错数字.
警误区 画数轴常出现的错误 (1)没有标明方向;(2)没有原点;(3)单位长度不一致;(4)负数的排列错误.
3.数轴上的点与有理数的关系
(1)数对应点:每一个有理数都可以用数轴上的点表示出来,整数可以直接找到对应的整数点,分数可以分成多少份(分母的份数),取其中的分子数份.
(2)点表示数:数轴上的每一个点都表示一个数(不仅仅是有理数).
(3)一一对应:每个点都表示唯一的一个数,每个数都有唯一的对应点.
(4)理解:①借助于数轴把数直观的排列在一条直线上,便于归类、比较.
②若设a为一个正数,则数轴上表示数a的点在原点的右边,与原点的距离是a个单位长度,表示-a的点在原点的左边,与原点的距离是a个单位长度.
谈重点 数轴上的点与有理数的关系 ( http: / / www.21cnjy.com ) 正数用原点右边的点表示,反过来原点右边的点都表示正数;负数用原点左边的点表示,反过来原点左边的点都表示负数;0用原点表示,原点表示0.
【例3】 下列语句:①数轴上的点仅 ( http: / / www.21cnjy.com )能表示整数;②数轴是一条直线;③数轴上的一个点只能表示一个数;④数轴上找不到既不表示正数,又不表示负数的点;⑤数轴上的点所表示的数都是有理数.正确的说法有( ).
A.1个 B.2个
C.3个 D.4个
解析:结合数轴上的点与有理数的特点,①是错误 ( http: / / www.21cnjy.com )的;④中可以含有0,⑤中应该是所有的有理数都可以在数轴上找出对应的点,但数轴上的点并不都表示有理数,以后学习的无理数也可以用数轴上的点表示.所以④、⑤也错误,只有②、③是正确的,故选B.
答案:B
所有有理数都可以在数轴上找到座位,但每个座位表示的数不一定是有理数.
4.相反数
(1)定义:只有符号不同的两个数叫做互为相反数.特别地,0的相反数是0.
(2)对称性:两个互为相反数的数,在数轴上的对应点(0除外),都在原点两旁,是距离原点相等的两个点.即:互为相反数的两个数在数轴上的对应点关于原点对称,这两点到原点的距离相等.
解技巧 相反数的求法 ① ( http: / / www.21cnjy.com )在正数前面添上一个“-”号,就得到这个正数的相反数,是一个负数;把负数前的“-”号去掉,就得到这个负数的相反数,是一个正数;②我们把a的相反数记为-a.a表示任意一个数,可以是正数、负数和0.
【例4】 3的相反数是_ ( http: / / www.21cnjy.com )_________,-5.8是______的相反数,a的相反数是______,a-b的相反数是______,0的相反数是______.
解析:只有符号不同的两个数互为相反数,所以只改变符号即可,其中a-b是一个数,是个整体,所以要加括号.
答案:-3 5.8 -a -(a-b) 0
5.运用相反数化简符号
(1)理解:在任意一个数前面添上“-”号,新的数就是原数的相反数.
如:+5的相反数表示为-(+5),而5 ( http: / / www.21cnjy.com )的相反数就是-5,所以-(+5)=-5;-5的相反数表示为-(-5),我们知道-5的相反数是5,所以-(-5)=5,因此运用相反数可以进行符号化简:-(-10)=10,-(+6)=-6等;
(2)分类:简单的符号化简共有3种情况:
①-(+a)=-a;②+(-a)=-a;③-(-a)=a.
(3)延伸:①-[-(-a)]=-a;-[+(-a)]=a等.②-0=0,表示0的相反数是0.
【例5】 化简下列各符号:
(1)-[-(-2)];
(2)+{-[-(+5)]};
(3)-{-{-…-(-6)}…}(共n个负号).
解析:化简的法则是:结果的符号与负号的个数有关,有偶数个负号时,结果为正;有奇数个负号时,结果为负.
答案:(1)-2;(2)5;(3)当n为偶数时,为6;当n为奇数时,为-6.
6.绝对值
(1)定义:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值.
(2)表示:数a的绝对值表示为|a|.
(3)求法:①一个正数的绝对值是它本身;
②一个负数的绝对值是它的相反数;
③0的绝对值是0.
用字母表示为:如果a>0,那么|a|=a;如果a=0,那么|a|=0;如果a<0,那么|a|=-a.
归纳为|a|=
谈重点 绝对值的理解 ①确定一个非零 ( http: / / www.21cnjy.com )数的绝对值首先应看这个数是正数还是负数,是正数则是它本身,是负数则是它的相反数,特别是字母表示的数更应先确定正负,再去绝对值号;②由定义可知,任何数的绝对值都是非负数,所以不存在绝对值是负数的数;③绝对值是一个正数的数有两个,它们互为相反数.
【例6】 绝对值为4的数是( ).
A.±4 B.4
C.-4 D.2
解析:绝对值是4的数有两个,+4和-4.
不要弄错哦,绝对值为一个正数的数有两个,它们互为相反数.
答案:A
7.数的大小的比较
(1)借助数轴比较数的大小:数轴上的点表示的数从左往右逐渐增大,并且右边的数总比左边的数大.
(2)正数、0、负数大小的比较:
正数大于0,0大于负数,正数大于负数.
(3)用绝对值比较两个负数的大小:
两个负数相比较,绝对值大的反而小.
解技巧 数的大小比较方法选择 数 ( http: / / www.21cnjy.com )的比较一般有四种情况:①正数、负数、0的比较,直接按法则;②正数之间的比较,符合小学认知,大就是大;③两个负数大小的比较,一是比较绝对值的大小,绝对值大的反而小,二是表示在数轴上比较大小,右边的数总比左边的大;④不是最简数,化为最简后再比较大小.
【例7】 用“>”“=”“<”填空:
①-7______-5;②-0.1______-0.01;
③______-;④0__________-3.14;
⑤______0.25;
⑥-|-3.2|______-(-3.2).
解析:③、④为正数、负数、0的大小比较, ( http: / / www.21cnjy.com )很显然③>-,④0>-3.14;①、②为两负数大小的比较,根据绝对值大的反而小知:①-7<-5;②-0.1<-0.01;⑤是两正数的比较,=0.25;⑥需要化简后比较,-|-3.2|=-3.2,-(-3.2)=3.2,所以-|-3.2|<-(-3.2).
答案:< < > > = <
谈重点 比较大小 异号两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑它们的绝对值.
8.有理数分类的应用延伸
(1)按照不同的分类方法,数可以分为不同的类,但是无论按哪种方法分类,都必须全面、严密,不重不漏;
(2)类似于某同学是某学校、某年级、 ( http: / / www.21cnjy.com )某班的学生一样,数的范围也有大小,比如:-8是有理数中的整数类,又是整数中的负整数,所以每个数既是大类别中的数,又归为不同的子类别;③目前所学数中π不是有理数.
破疑点 0的理解 ①0既不是正数也不 ( http: / / www.21cnjy.com )是负数,它是有理数,是整数,也是自然数;②0和正整数统称为自然数,没有负自然数;③整数和分数中有正整数、0、负整数、正分数、负分数之分.
【例8】 在下表适当的空格里画上“√”号.
有理数 整数 分数 正整数 负分数 自然数
-9是
-2.35是
0是
+5是
分析:正是由于数的范围大小不同 ( http: / / www.21cnjy.com ),所以数归为不同的类.如:-9是有理数,也是整数、是整数中的负整数,-2.35是有理数,也是分数,是分数中的负分数.
解:
有理数 整数 分数 正整数 负分数 自然数
-9是 √ √
-2.35是 √ √ √
0是 √ √ √
+5是 √ √ √ √
9.绝对值的化简和计算
化简绝对值符号主要根据绝对值的非负性,解题时看清楚“-”号在绝对值符号的里面还是外面.如果“-”号在绝对值符号的里面,化简时把“-”号去掉;如果“-”号在绝对值符号的外面,化简时不能把“-”号去掉.
解技巧 去绝对值的关键 化简绝对值符号的关键是判断绝对值符号内的数是正数还是负数.
【例9】 化简(1)-;(2)+|-24|;
(3);(4)|-(-7.5)|.
分析:先判断数的符号,再求绝对值.
解:(1)-=-;
(2)+|-24|=24;
(3)=3;
(4)|-(-7.5)|=7.5.
10.数轴上两点间的距离与点表示的数之间的关系
(1)数轴使数和直线上的点建立了对应关系,它揭示了数和形的内在联系;正是这种联系,使得数轴上两点之间的距离与所表示的数之间存在密切关系.
(2)数轴上表示数a的点与原点之间的距 ( http: / / www.21cnjy.com )离:当a为一个正数时,它与原点的距离是a个单位长度,当a是负数时,它与原点的距离是|a|个单位长度;当a是0时,距离为0;
(3)注意:到某一点距离等于a(a是正数)的点有两个,在点的左右两侧各一个.
解技巧 数形结合求距离 解决此类问题的最好方法是画出数轴,并表示出所求的数,再求两点间的距离.
【例10-1】 在数轴上,表示-2的点与原点的距离是__________;表示的点与原点的距离是__________.
解析:-2在原点的左侧,到原点的距离是2个单位长度,到原点的距离是个单位长度.
答案:2
【例10-2】 数轴上点A到原点0的距离等于6,点B到原点0的距离等于4,则A,B两点之间的最大距离是__________.
解析:如图,
在数轴上,A点到原点的距离是6,所以A点可 ( http: / / www.21cnjy.com )以是-6,6表示的点,即图中的A1,A2点,B点是-4,4表示的点,即B1,B2点,A,B两点之间的最大距离就是A1B2或A2B1的长度,它们相等,都是6+4=10,所以A,B两点之间的最大距离是10个单位长度.
答案:10
11.字母表示的数的绝对值的求法应用
因为用字母所表示的数既可以是 ( http: / / www.21cnjy.com )正数也可以是负数,还可以是0,它具有不确定性,而求绝对值首先要考虑的就是符号,因此求字母表示的数的绝对值时,必须考虑题目中给定的条件,若有限定条件,就按限定条件求出,若没有限定条件,则要分正、负、0三种情况讨论.
解技巧 绝对值的求法 ①限制型逆用求 ( http: / / www.21cnjy.com )法,如:|a|=6,那么a=±6;②开放型分类讨论求法:如求|x|+x的值,当x>0时,|x|=x,所以|x|+x=x+x=2x,当x<0时,|x|=-x,原式=0,当x=0时,原式=0.③化简型求法:如:|a|=|-8|,|-a|=|-8|,|-a|=|8|都能化为|a|=|8|=8解决.
【例11-1】 如果|a|=5,|b|=4,a<b,那么a=__________,b=__________.
解析:因为±5的绝对值都是5,所以a= ( http: / / www.21cnjy.com )+5或-5,同样由|b|=4得b=±4,当a=-5时,-5<4,-5<-4,所以b=±4都能使a<b成立,而当a=5时,5>4,5>-4,所以b=±4都不能满足条件a<b,所以a=-5,b=±4.
答案:-5 ±4
【例11-2】 若|a|=|b|,则a,b的关系是( ).
A.a=b B.a=-b
C.a=b或a=-b D.a=0且b=0
解析:方法一:因为绝对值相等,所以数a,b就数字部分看(不考虑符号)应该完全相同,只是符号有正、负两种情况,组合会有4种情况,当同正或同负时,两数的符号相同,数字部分又完全一样,所以相等,即a=b,异号时,两数只有符号不同,所以两数互为相反数,即a=-b,所以两数要么相等,要么互为相反数,故选C.
方法二:此题还可以选择一些特殊的值,如a ( http: / / www.21cnjy.com )=2,3,5,…,那么相对应的b=±2,±3,±5,…,从而得到a与b的值同号时相等,异号时互为相反数,即a=b或a=-b.
答案:C
12.利用数轴解决生活中的实际问题
本节知识常与运动问题结合在一起,利用数形结合将运动问题解决.这种利用数形结合解决问题的方法是中考考查的热点题型之一.
数轴是一种数学工具,它使数和数轴上的点建立了 ( http: / / www.21cnjy.com )对应关系,揭示了数与形之间的内在联系,也为我们研究问题提供了新的方法.数轴是联系数与形的桥梁,是数形结合的具体体现,利用数轴可以解决生活中的许多问题.
运用数轴可以直观表示点的移动,正确找出数在数轴上的对应点,会由数轴上的点的位置确定对应的数,是解决这类问题的关键.
【例12】 超市、书店、玩具店依次坐 ( http: / / www.21cnjy.com )落在一条东西走向的大街上,超市在书店西边20米处,玩具店位于书店东边50米处.小明从书店出来沿街向东走了50米,接着又向东走了-80米,此时小明的位置在何处?在数轴上标出超市、书店、玩具店的位置,以及小明最后的位置.
分析:书店处于超市和玩具店之间,且书店 ( http: / / www.21cnjy.com )与玩具店之间的距离是50米,书店与超市之间的距离是20米,这样可以画出数轴,即可表示出小明最后的位置.
解决点的移动问题,可画出数轴,在数轴上表 ( http: / / www.21cnjy.com )示点的移动,关键是确定原点,最后的点相对于原点来说,若在原点的右侧,表示的是正数,若在原点的左侧,则表示的是负数.
解:根据题意可以画出如图所示的数轴,小明位于超市西边10米处.
13.利用绝对值解决实际问题
绝对值的产生来源于实际问题的需要,反过来又可以运用它解决一些实际问题,主要有以下两类:
(1)判断物体或产品的质量
用绝对值判断物体或产品偏离标准的程度,绝对值越小,越接近标准,质量就越好.
方法:①求每个数的绝对值;
②比较所求绝对值的大小;
③根据“绝对值小的越接近标准”作出判断.
(2)利用绝对值求距离
路程问题中,当出现用“+”“-”号表示带方向的路程,求最后实际路程时,实际上是求绝对值的和.
方法:
①求各个数的绝对值;
②求所有数的绝对值的和;
③写出答案.
【例13-1】 某汽车配件厂生产一 ( http: / / www.21cnjy.com )批圆形的橡胶垫,从中抽取6件进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查结果如下:
1 2 3 4 5 6
+0.5 -0.3 +0.15 -0.1 0 0.2
用绝对值的知识说明哪个零件的质量最好?
分析:质量的好坏取决于质量偏离标准质量的绝对值,即偏离橡胶垫的标准质量的绝对值越小,越接近标准,其质量就越好.
解:因为|+0.5|>|-0.3|>|0.2|>|+0.15|>|-0.1|>|0|,
所以第5个零件的质量最好.
【例13-2】 一天上午,出租车司机 ( http: / / www.21cnjy.com )小王在东西走向的中山路上运营,如果规定向东为正,向西为负,出租车的行车里程如下(单位:千米):+15,-3,+12,-11,-13,+3,-12,-18,请问小王将最后一位乘客送到目的地时,共行驶了多少千米?
解:|+15|+|-3|+|+12|+ ( http: / / www.21cnjy.com )|-11|+|-13|+|+3|+|-12|+|-18|=15+3+12+11+13+3+12+18=87(千米).
答:小王将最后一位乘客送到目的地时共行驶了87千米.
14.特殊值法的妙用
(1)作用:字母表示数是代数 ( http: / / www.21cnjy.com )的核心,用字母表示数为我们研究数学规律和方法提供了很多便利,但由于字母表示数的抽象性和不确定性,使含有字母的数的运算和大小的比较,变的复杂且不容易理解,取特殊值法为我们提供了简便的解法,也便于理解.同时也揭示出由特殊到一般的探索过程.
(2)方法技巧:①特殊值法 ( http: / / www.21cnjy.com )取特殊值时,所取的值一定要符合题目要求,在所规定的范围内;②要尽量简便,一般选取较小或较简单的数,以简化计算过程;③取适当的个数,并且按一定规律或顺序取值,以便于发现规律,正确解决问题;④赋值要全面,要考虑周全,考虑各种适合的可能,这也是特殊值法得到的结论是否正确的关键.特别要注意一些特殊数,如:0,±1等.如例142中要按大于1,等于1,小于1三种情况分类讨论取值,从而全面了解了在x为正数条件下的各种情况.
【例14-1】 若a<0,b>0,且|a|<|b|,试用“<”号连接a,b,-a,-b.
分析:常规解法要考虑各数值的正负,还要考虑 ( http: / / www.21cnjy.com )绝对值的大小,借助于数轴解决.但用特殊值法,在满足a<0,b>0,且|a|<|b|的条件下,可以取a=-2,b=5,这时,-a=2,-b=-5,由于-5<-2<2<5,所以-b<a<-a<b;同样可以再取一次别的数,当a=-6,b=7时,-a=6,-b=-7,由于-7<-6<6<7,所以-b<a<-a<b;由此可知四个数的大小关系是-b<a<-a<b.
解:-b<a<-a<b.
【例14-2】 若x是正数,试比较x与的大小.
分析:分三种情况列举取值,当x=1时,x的倒 ( http: / / www.21cnjy.com )数=1,倒数等于原数,即x=;当x=2,3,4,…时,x的倒数分别为,,,…,此时原数都大于它的倒数,即x>;当x=,,,…,或取小数0.6,0.7,…时,x的倒数分别为:2,3,,…,或,…,此时原数都小于倒数,即x<,因此以1为分界,包括1,共三种情况.
解:当x>1时,x>;当x=1时,x=;当x<1时,x<.
15.借助数轴比较数的大小的应用
对于简单的数的比较,如正数之间,正负数、0之间数的大小的比较可以直接写出,但对于较多的数,或复杂的数的比较,有时候借助数轴会更简单,更直观,也便于理解,
(1)依据:数轴上的点表示的数,右边的总比左边的大.
(2)分类:①具体的数的大小的比较,初学负数,特别是对于多个相近负数的比较,运用数轴会更准确、直观.同时能培养学生的数感.
②字母表示的数的大小的比较:根据数轴上字母表 ( http: / / www.21cnjy.com )示的数的位置,根据相反数、绝对值意义,标出所求数的位置(所求数表示的点),再根据数轴上的点所表示数的大小规律,写出所求数的大小关系.
【例15-1】 比较下列各数的大小:
-1.5,-0.5,-3.5,-5.
解:将这些数在数轴上表示出来,如图,
从数轴上可以看出-5<-3.5<-1.5<-0.5.
【例15-2】 数a,b在数轴上的位置如图所示,下面所给的四个选项中正确的是( ).
A.b>a B.|a|>|b|
C.-a<b D.-b>a
解析:因为a>0,b<0,所 ( http: / / www.21cnjy.com )以b<a,故排除A;因为表示b的点到原点的距离比表示a的点到原点的距离大,根据绝对值的定义可得|a|<|b|,故排除B;在数轴上将-a、-b的位置表示出来,如图所示,
显然有b<-a<0<a<-b,故排除C,故只有D正确.
答案:D
