苏教版选择性必修第一册第3章 圆锥曲线与方程 章末复习提升 课件(共23张PPT)
文档属性
| 名称 | 苏教版选择性必修第一册第3章 圆锥曲线与方程 章末复习提升 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 856.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-24 21:49:17 | ||
图片预览








文档简介
(共23张PPT)
章末复习提升
第3章 圆锥曲线与方程
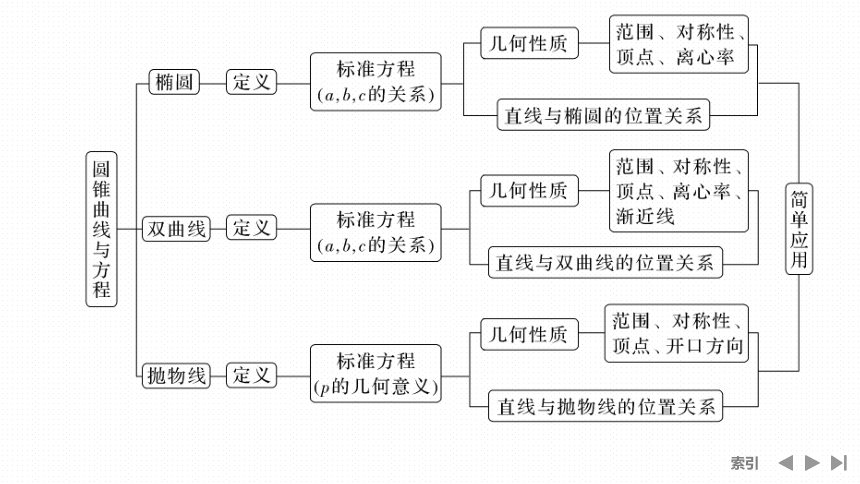
网络构建
形成体系
内容
索引
要点聚焦
类型突破
WANG LUO GOU JIAN XING CHENG TI XI
网络构建 形成体系
1
2
YAO DIAN JU JIAO LEI XING TU PO
要点聚焦 类型突破
要点一 圆锥曲线的定义及应用
圆锥曲线的定义是相应标准方程和几何性质的“源”,对于圆锥曲线的有关问题,要有运用圆锥曲线定义解题的意识,“回归定义”是一种重要的解题策略.
研究与圆锥曲线有关的两点间的距离的最值问题时,常用定义把曲线上的点到焦点的距离转化为到另一焦点的距离或利用定义把曲线上的点到焦点的距离转化为其到相应准线的距离,再利用数形结合的思想去解决问题.
C
∴动点M到原点的距离与它到直线3x+4y-12=0的距离相等.
∴点M的轨迹是以原点为焦点,直线3x+4y-12=0为准线的抛物线.
(2)双曲线16x2-9y2=144的左、右两焦点分别为F1,F2,点P在双曲线上,且PF1·PF2=64,则∠F1PF2=________.
60°
所以a2=9,b2=16,所以c2=25,
解得a=3,c=5,所以F1(-5,0),F2(5,0).
设PF1=m,PF2=n,
由双曲线的定义知|m-n|=2a=6,
又已知m·n=64,
训练1 已知抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若2BF=AF+CF,则( )
A.2x2=x1+x3 B.2y2=y1+y3
C.2x3=x1+x2 D.2y3=y1+y22
A
解析 如图,过A,B,C分别作准线的垂线,垂足分别为A′,B′,C′,由抛物线定义知
AF=AA′,BF=BB′,CF=CC′.
∵2BF=AF+CF,∴2BB′=AA′+CC′.
要点二 圆锥曲线的方程与性质
椭圆、双曲线、抛物线的几何性质,主要指图形的范围、对称性,以及顶点坐标、焦点坐标、中心坐标、离心率、准线、渐近线以及几何元素a,b,c,e之间的关系等.
3
要点三 直线与圆锥曲线的位置关系
(1)公共点的个数问题,应注意数形结合;
(2)弦长问题,应注意运用弦长公式及根与系数的关系;
(3)垂直问题,应注意运用斜率关系及根与系数的关系,尽量设而不求,简化运算.
(4)面积问题,应注意面积的计算方法,可以运用定义整体求解.对于三角形如果底和高不便于计算,还可以利用割补法考虑拆分成若干个易于计算的三角形再计算.
`xc
∴|x2-x1|=2.
联立mx2+ny2=1与x+y-1=0
可得(m+n)x2-2nx+n-1=0,
且由已知得x1,x2是方程(m+n)x2-2nx+n-1=0的两根,
得(m+n)x2-2nx+n-1=0.
设A(x1,y1),B(x2,y2),
`xc
本课结束
章末复习提升
第3章 圆锥曲线与方程
网络构建
形成体系
内容
索引
要点聚焦
类型突破
WANG LUO GOU JIAN XING CHENG TI XI
网络构建 形成体系
1
2
YAO DIAN JU JIAO LEI XING TU PO
要点聚焦 类型突破
要点一 圆锥曲线的定义及应用
圆锥曲线的定义是相应标准方程和几何性质的“源”,对于圆锥曲线的有关问题,要有运用圆锥曲线定义解题的意识,“回归定义”是一种重要的解题策略.
研究与圆锥曲线有关的两点间的距离的最值问题时,常用定义把曲线上的点到焦点的距离转化为到另一焦点的距离或利用定义把曲线上的点到焦点的距离转化为其到相应准线的距离,再利用数形结合的思想去解决问题.
C
∴动点M到原点的距离与它到直线3x+4y-12=0的距离相等.
∴点M的轨迹是以原点为焦点,直线3x+4y-12=0为准线的抛物线.
(2)双曲线16x2-9y2=144的左、右两焦点分别为F1,F2,点P在双曲线上,且PF1·PF2=64,则∠F1PF2=________.
60°
所以a2=9,b2=16,所以c2=25,
解得a=3,c=5,所以F1(-5,0),F2(5,0).
设PF1=m,PF2=n,
由双曲线的定义知|m-n|=2a=6,
又已知m·n=64,
训练1 已知抛物线y2=2px(p>0)上有A(x1,y1),B(x2,y2),C(x3,y3)三点,F是它的焦点,若2BF=AF+CF,则( )
A.2x2=x1+x3 B.2y2=y1+y3
C.2x3=x1+x2 D.2y3=y1+y22
A
解析 如图,过A,B,C分别作准线的垂线,垂足分别为A′,B′,C′,由抛物线定义知
AF=AA′,BF=BB′,CF=CC′.
∵2BF=AF+CF,∴2BB′=AA′+CC′.
要点二 圆锥曲线的方程与性质
椭圆、双曲线、抛物线的几何性质,主要指图形的范围、对称性,以及顶点坐标、焦点坐标、中心坐标、离心率、准线、渐近线以及几何元素a,b,c,e之间的关系等.
3
要点三 直线与圆锥曲线的位置关系
(1)公共点的个数问题,应注意数形结合;
(2)弦长问题,应注意运用弦长公式及根与系数的关系;
(3)垂直问题,应注意运用斜率关系及根与系数的关系,尽量设而不求,简化运算.
(4)面积问题,应注意面积的计算方法,可以运用定义整体求解.对于三角形如果底和高不便于计算,还可以利用割补法考虑拆分成若干个易于计算的三角形再计算.
`xc
∴|x2-x1|=2.
联立mx2+ny2=1与x+y-1=0
可得(m+n)x2-2nx+n-1=0,
且由已知得x1,x2是方程(m+n)x2-2nx+n-1=0的两根,
得(m+n)x2-2nx+n-1=0.
设A(x1,y1),B(x2,y2),
`xc
本课结束
