人教版高中数学必修第一册第四章 函数应用 章末复习课课件(共25张PPT)
文档属性
| 名称 | 人教版高中数学必修第一册第四章 函数应用 章末复习课课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第四章 函数应用
章末复习课
1.体会函数与方程之间的联系,会用二分法求方程的近似解;
2.了解指数函数、幂函数、对数函数的增长差异;
3.巩固建立函数模型的过程和方法,了解函数模型的广泛应用.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
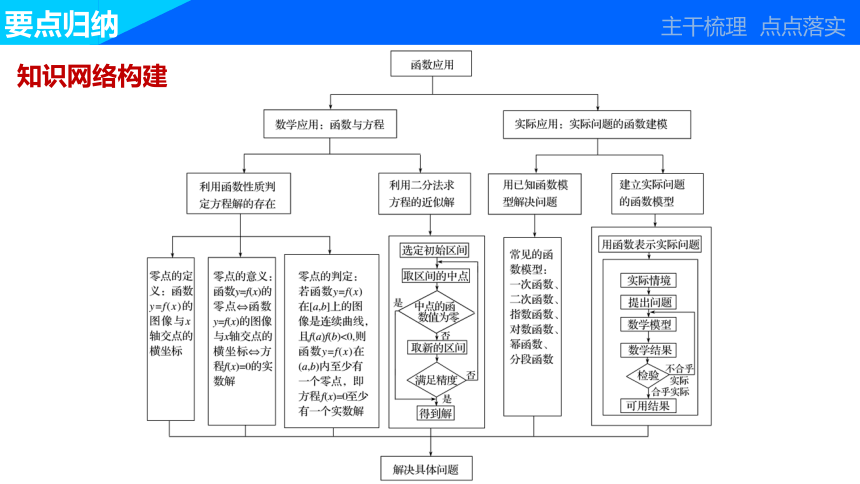
知识网络构建
知识方法回顾
1.函数的零点与方程的根的关系:
(1)方程f(x)=0有实数根 函数 的图像与 有交点 有零点.
(2)确定函数零点的个数有两个基本方法:
①借助函数 性和 定理研究图像与x轴的交点个数;
②通过移项,变形转化成 个函数图像的交点个数进行判断.
答案
y=f(x)
x轴
函数y=f(x)
单调
零点存在性
两
2.二分法
(1)图像都在x轴同侧的函数零点 (填“能”或“不能”)用二分法求.
(2)用二分法求零点近似解时,零点区间(a,b)始终要保持f(a)·f(b) 0;
(3)若要求精度为0.01,则当|a-b| 0.01时,便可判断零点近似值为 .
3.函数模型
(1)给定函数模型与拟合函数模型中求函数解析式主要使用 法.
(2)建立确定性的函数模型的基本步骤是_______________________________
___________.
(3)所有的函数模型问题都应注意变量的实际意义对 的影响.
返回
答案
不能
<
<
a(或b)
待定系数
审题,设量,表示条件,整理化简,
标明定义域
定义域
类型一 函数的零点与方程的根的关系及应用
例1 设g(x)=e2x+|ex-a|,x∈[0,ln 3],其中a≤2 ,
(1)当a=1时,函数g(x)是否存在零点,若存在,求出所有零点;若不存在,说明理由.
解 当a=1时,设t=ex(显然t∈[1,3]),
则h(t)=t2+t-1,令h(t)=t2+t-1=0,
题型探究 重点难点 个个击破
解析答案
∴函数g(x)不存在零点.
(2)求函数g(x)的最小值.
解 设t=ex,则h(t)=t2+|t-a|(显然t∈[1,3]).
当a≤1时,h(t)=t2+t-a在区间[1,3]上是增函数,
所以h(x)的最小值为h(1)=2-a.
解析答案
因为函数h(t)在区间(a,3]上是增函数,在区间[1,a]上也是增函数,
又函数h(t)在[1,3]上为连续函数,
所以h(t)的最小值为h(1)=a.
综上可得:当a≤1时,g(x)的最小值为2-a;
所以函数h(t)在[1,3]上为增函数,
反思与感悟
(1)函数的零点与方程的根的关系:方程f(x)=0有实数根 函数y=f(x)的图像与x轴有交点 函数y=f(x)有零点.
(2)确定函数零点的个数有两个基本方法:利用图像研究与x轴的交点个数或转化成两个函数图像的交点个数进行判断.
反思与感悟
解析答案
跟踪训练1 若函数f(x)的零点与g(x)=4x+2x-2的零点之差的绝对值不超过0.25,则函数f(x)可以是( )
A.f(x)=4x-1 B.f(x)=(x-1)2
C.f(x)=ex-1 D.f(x)=ln(x-1)
f(x)=(x-1)2的零点为1,f(x)=ex-1的零点为0,f(x)=ln(x-1)的零点为2,
A
类型二 用二分法求函数的零点或方程的近似解
例2 用二分法求3x2-4x-1=0的近似解(精度0.1).
解析答案
反思与感悟
解 令f(x)=3x2-4x-1,作出函数图像如图所示,
观察图像知方程的一根x0∈(-1,0),另一根x0′∈(1,2),
且f(-1)=6,f(0)=-1,f(1)=-2,f(2)=3.
则f(-0.5)=1.75,所以f(-0.5)·f(0)<0,故x0∈(-0.5,0).
再取区间(-0.5,0)的中点x2=-0.25,
则f(-0.25)≈0.19,所以f(-0.25)·f(0)<0,故x0∈(-0.25,0).
再取区间(-0.25,0)的中点x3=-0.125,
则f(-0.125)≈-0.45,
所以f(-0.125)·f(-0.25)<0,故x0∈(-0.25,-0.125).
解析答案
反思与感悟
再取区间(-0.25,-0.125)的中点x4=-0.187 5,
则f(-0.187 5)≈-0.14,
所以f(-0.25)·f(-0.187 5)<0,
故x0∈(-0.25,-0.187 5).
又因为|0.25-0.187 5|=0.062 5<0.1,
所以-0.187 5为方程3x2-4x-1=0的一个根的近似值.
同理:当x0′∈(1,2)时,方程的根的近似值为1.562 5.
综上所述,方程3x2-4x-1=0的根的近似值为-0.187 5和1.562 5.
反思与感悟
(1)看清题目的精度,它决定着二分法的结束.
(2)根据f(a0)·f(b0)<0确定初始区间,高次方程要先确定有几个解再确定初始区间.
(3)初始区间的选定一般在两个整数间,不同初始区间结果是相同的,但二分的次数相差较大.
(4)取区间中点c,计算中点函数值f(c),确定新的零点区间,直到所取区间(an,bn)中,|an-bn|≤ε,那么区间(an,bn)内任意一个数都是满足精度ε的近似解.
反思与感悟
跟踪训练2 某方程在区间[0,1]内有一无理根,若用二分法求此根的近似值,要使所得近似值的精度达到0.1,则将区间(0,1)分( )
A.2次 B.3次
C.4次 D.5次
解析 等分1次,区间长度为0.5;
等分两次,区间长度为0.25;
…;
等分4次,区间长度为0.062 5<0.1,符合题意.
解析答案
C
类型三 函数模型及应用
例3 在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R与管道半径r的函数关系为R=kr4(k>0,k是常数).
(1)假设气体在半径为3 cm的管道中,流量速率为400 cm3/s,求该气体通过半径为r cm的管道时,其流量速率R的表达式;
解 由题意,得R=kr4(k是大于0的常数).
由r=3 cm,R=400 cm3/s,得k·34=400,
解析答案
(2)已知(1)中的气体通过的管道半径为5 cm,计算该气体的流量速率.
解析答案
即气体通过管道半径为5 cm时,该气体的流量速率约为3 086 cm3/s.
反思与感悟 一旦选定函数模型,下面的工作就是挖掘题目条件求出待定系数.
反思与感悟
跟踪训练3 为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为y= t-a(a为常数),如图,根据图中所提供的信息,回答下列问题:
(1)从药物释放开始,每立方米空气中的含药量y(毫克)
与时间t(小时)之间的函数关系式为_______________.
解析 由题意和图示知,当0≤t≤0.1时,
可设y=kt(k为待定系数),由于点(0.1,1)在直线上,∴k=10;
解析答案
返回
解析答案
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过____小时后,学生才能回到教室.
解析 由题意可得 得t>0.6,
即至少需要经过0.6小时后,学生才能回到教室.
0.6
1
2
3
1.已知函数f(x)=ax-x-a(a>0,a≠1),那么函数f(x)的零点个数是( )
A.0个 B.1个
C.2个 D.至少1个
解析 在同一坐标系中作出函数
y=ax与y=x+a的图像,
当a>1时,如图(1),
当0故选D.
达标检测
4
D
解析答案
5
2.用二分法求如图所示函数f(x)的零点时,不可能求出的零点是( )
A.x1 B.x2 C.x3 D.x4
C
答案
1
2
3
4
5
3.在一次数学试验中,采集到如下一组数据:
x -2 -1 0 1 2 3
y 0.24 0.51 1 2.02 3.98 8.02
则下列函数与x,y的函数关系是最接近的是(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+
答案
B
1
2
3
4
5
(log32,1)
答案
5.已知方程2x=10-x的根x∈(k,k+1),k∈Z,则k=____.
2
1
2
3
4
5
1.对于零点性质要注意函数与方程的结合,借助零点的性质可研究函数的图像、确定方程的根;对于连续函数,利用零点存在性定理,可用来求参数的取值范围.
2.函数模型的应用实例的基本题型
(1)给定函数模型解决实际问题;
(2)建立确定的函数模型解决问题;
(3)建立拟合函数模型解决实际问题.
规律与方法
3.函数建模的基本过程如图
返回
本课结束
第四章 函数应用
章末复习课
1.体会函数与方程之间的联系,会用二分法求方程的近似解;
2.了解指数函数、幂函数、对数函数的增长差异;
3.巩固建立函数模型的过程和方法,了解函数模型的广泛应用.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
知识网络构建
知识方法回顾
1.函数的零点与方程的根的关系:
(1)方程f(x)=0有实数根 函数 的图像与 有交点 有零点.
(2)确定函数零点的个数有两个基本方法:
①借助函数 性和 定理研究图像与x轴的交点个数;
②通过移项,变形转化成 个函数图像的交点个数进行判断.
答案
y=f(x)
x轴
函数y=f(x)
单调
零点存在性
两
2.二分法
(1)图像都在x轴同侧的函数零点 (填“能”或“不能”)用二分法求.
(2)用二分法求零点近似解时,零点区间(a,b)始终要保持f(a)·f(b) 0;
(3)若要求精度为0.01,则当|a-b| 0.01时,便可判断零点近似值为 .
3.函数模型
(1)给定函数模型与拟合函数模型中求函数解析式主要使用 法.
(2)建立确定性的函数模型的基本步骤是_______________________________
___________.
(3)所有的函数模型问题都应注意变量的实际意义对 的影响.
返回
答案
不能
<
<
a(或b)
待定系数
审题,设量,表示条件,整理化简,
标明定义域
定义域
类型一 函数的零点与方程的根的关系及应用
例1 设g(x)=e2x+|ex-a|,x∈[0,ln 3],其中a≤2 ,
(1)当a=1时,函数g(x)是否存在零点,若存在,求出所有零点;若不存在,说明理由.
解 当a=1时,设t=ex(显然t∈[1,3]),
则h(t)=t2+t-1,令h(t)=t2+t-1=0,
题型探究 重点难点 个个击破
解析答案
∴函数g(x)不存在零点.
(2)求函数g(x)的最小值.
解 设t=ex,则h(t)=t2+|t-a|(显然t∈[1,3]).
当a≤1时,h(t)=t2+t-a在区间[1,3]上是增函数,
所以h(x)的最小值为h(1)=2-a.
解析答案
因为函数h(t)在区间(a,3]上是增函数,在区间[1,a]上也是增函数,
又函数h(t)在[1,3]上为连续函数,
所以h(t)的最小值为h(1)=a.
综上可得:当a≤1时,g(x)的最小值为2-a;
所以函数h(t)在[1,3]上为增函数,
反思与感悟
(1)函数的零点与方程的根的关系:方程f(x)=0有实数根 函数y=f(x)的图像与x轴有交点 函数y=f(x)有零点.
(2)确定函数零点的个数有两个基本方法:利用图像研究与x轴的交点个数或转化成两个函数图像的交点个数进行判断.
反思与感悟
解析答案
跟踪训练1 若函数f(x)的零点与g(x)=4x+2x-2的零点之差的绝对值不超过0.25,则函数f(x)可以是( )
A.f(x)=4x-1 B.f(x)=(x-1)2
C.f(x)=ex-1 D.f(x)=ln(x-1)
f(x)=(x-1)2的零点为1,f(x)=ex-1的零点为0,f(x)=ln(x-1)的零点为2,
A
类型二 用二分法求函数的零点或方程的近似解
例2 用二分法求3x2-4x-1=0的近似解(精度0.1).
解析答案
反思与感悟
解 令f(x)=3x2-4x-1,作出函数图像如图所示,
观察图像知方程的一根x0∈(-1,0),另一根x0′∈(1,2),
且f(-1)=6,f(0)=-1,f(1)=-2,f(2)=3.
则f(-0.5)=1.75,所以f(-0.5)·f(0)<0,故x0∈(-0.5,0).
再取区间(-0.5,0)的中点x2=-0.25,
则f(-0.25)≈0.19,所以f(-0.25)·f(0)<0,故x0∈(-0.25,0).
再取区间(-0.25,0)的中点x3=-0.125,
则f(-0.125)≈-0.45,
所以f(-0.125)·f(-0.25)<0,故x0∈(-0.25,-0.125).
解析答案
反思与感悟
再取区间(-0.25,-0.125)的中点x4=-0.187 5,
则f(-0.187 5)≈-0.14,
所以f(-0.25)·f(-0.187 5)<0,
故x0∈(-0.25,-0.187 5).
又因为|0.25-0.187 5|=0.062 5<0.1,
所以-0.187 5为方程3x2-4x-1=0的一个根的近似值.
同理:当x0′∈(1,2)时,方程的根的近似值为1.562 5.
综上所述,方程3x2-4x-1=0的根的近似值为-0.187 5和1.562 5.
反思与感悟
(1)看清题目的精度,它决定着二分法的结束.
(2)根据f(a0)·f(b0)<0确定初始区间,高次方程要先确定有几个解再确定初始区间.
(3)初始区间的选定一般在两个整数间,不同初始区间结果是相同的,但二分的次数相差较大.
(4)取区间中点c,计算中点函数值f(c),确定新的零点区间,直到所取区间(an,bn)中,|an-bn|≤ε,那么区间(an,bn)内任意一个数都是满足精度ε的近似解.
反思与感悟
跟踪训练2 某方程在区间[0,1]内有一无理根,若用二分法求此根的近似值,要使所得近似值的精度达到0.1,则将区间(0,1)分( )
A.2次 B.3次
C.4次 D.5次
解析 等分1次,区间长度为0.5;
等分两次,区间长度为0.25;
…;
等分4次,区间长度为0.062 5<0.1,符合题意.
解析答案
C
类型三 函数模型及应用
例3 在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R与管道半径r的函数关系为R=kr4(k>0,k是常数).
(1)假设气体在半径为3 cm的管道中,流量速率为400 cm3/s,求该气体通过半径为r cm的管道时,其流量速率R的表达式;
解 由题意,得R=kr4(k是大于0的常数).
由r=3 cm,R=400 cm3/s,得k·34=400,
解析答案
(2)已知(1)中的气体通过的管道半径为5 cm,计算该气体的流量速率.
解析答案
即气体通过管道半径为5 cm时,该气体的流量速率约为3 086 cm3/s.
反思与感悟 一旦选定函数模型,下面的工作就是挖掘题目条件求出待定系数.
反思与感悟
跟踪训练3 为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为y= t-a(a为常数),如图,根据图中所提供的信息,回答下列问题:
(1)从药物释放开始,每立方米空气中的含药量y(毫克)
与时间t(小时)之间的函数关系式为_______________.
解析 由题意和图示知,当0≤t≤0.1时,
可设y=kt(k为待定系数),由于点(0.1,1)在直线上,∴k=10;
解析答案
返回
解析答案
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那么从药物释放开始,至少需要经过____小时后,学生才能回到教室.
解析 由题意可得 得t>0.6,
即至少需要经过0.6小时后,学生才能回到教室.
0.6
1
2
3
1.已知函数f(x)=ax-x-a(a>0,a≠1),那么函数f(x)的零点个数是( )
A.0个 B.1个
C.2个 D.至少1个
解析 在同一坐标系中作出函数
y=ax与y=x+a的图像,
当a>1时,如图(1),
当0
达标检测
4
D
解析答案
5
2.用二分法求如图所示函数f(x)的零点时,不可能求出的零点是( )
A.x1 B.x2 C.x3 D.x4
C
答案
1
2
3
4
5
3.在一次数学试验中,采集到如下一组数据:
x -2 -1 0 1 2 3
y 0.24 0.51 1 2.02 3.98 8.02
则下列函数与x,y的函数关系是最接近的是(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+
答案
B
1
2
3
4
5
(log32,1)
答案
5.已知方程2x=10-x的根x∈(k,k+1),k∈Z,则k=____.
2
1
2
3
4
5
1.对于零点性质要注意函数与方程的结合,借助零点的性质可研究函数的图像、确定方程的根;对于连续函数,利用零点存在性定理,可用来求参数的取值范围.
2.函数模型的应用实例的基本题型
(1)给定函数模型解决实际问题;
(2)建立确定的函数模型解决问题;
(3)建立拟合函数模型解决实际问题.
规律与方法
3.函数建模的基本过程如图
返回
本课结束
