2.3.4 等腰(边)三角形的判定同步练习(含解析)
文档属性
| 名称 | 2.3.4 等腰(边)三角形的判定同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 09:20:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
3 简单的轴对称图形
第4课时 等腰(边)三角形的判定
基础夯实
知识点一 等腰三角形的判定
1.在△ABC中,已知∠B=∠C,则( )
A. AB=BC B. AB=AC C. BC=AC D.∠A=60°
2.满足下列条件的三角形:①内角比为1:2:1;②内角比为2:2:5;③内角比为1:1:1;
④内角比为1:2:3.其中是等腰三角形的有____________.(填写序号)
3.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是___________.
4.如图,已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB,AC的中点.试说明:BE=CD.
知识点二 等边三角形的判定
5.在△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.若一个三角形中有两个角的平分线,分别垂直于该角所对的边,则这个三角形是( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
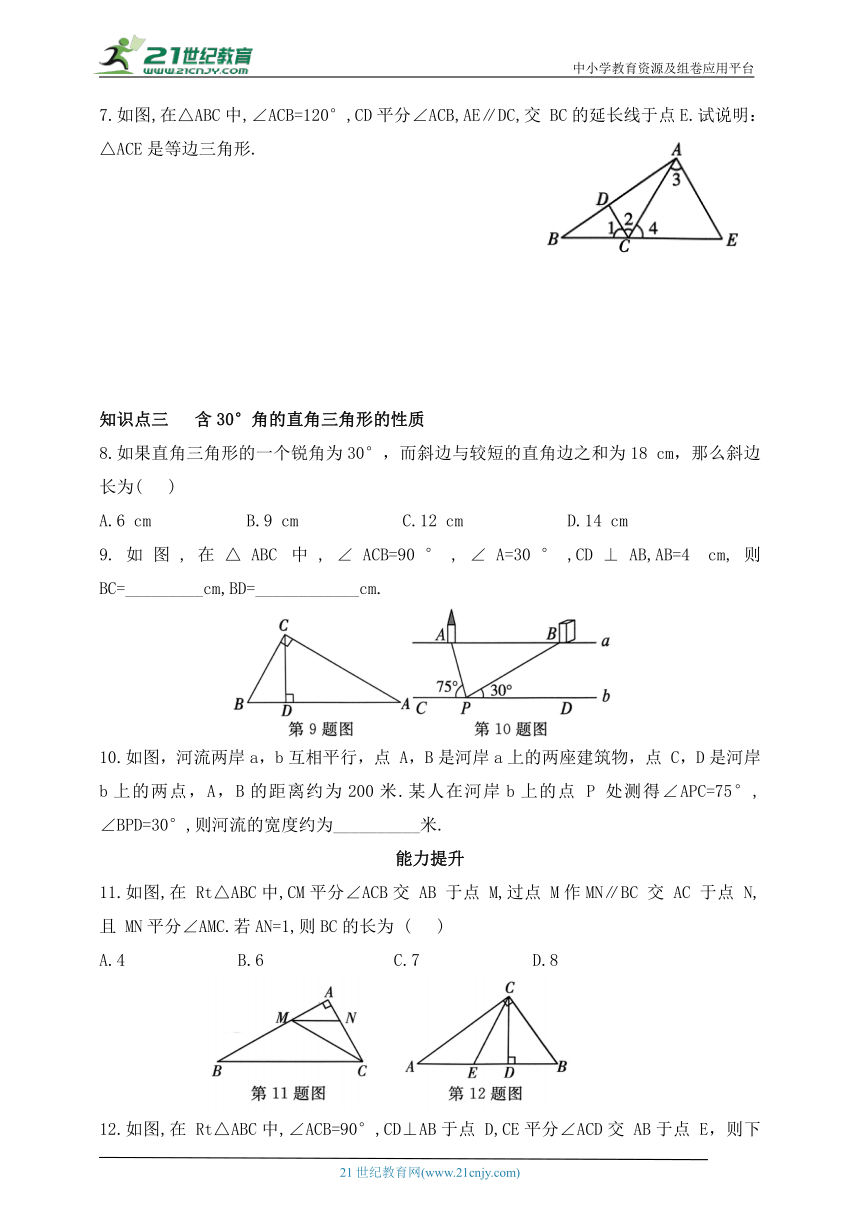
7.如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交 BC的延长线于点E.试说明:△ACE是等边三角形.
知识点三 含30°角的直角三角形的性质
8.如果直角三角形的一个锐角为30°,而斜边与较短的直角边之和为18 cm,那么斜边长为( )
A.6 cm B.9 cm C.12 cm D.14 cm
9.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,AB=4 cm,则 BC=_________cm,BD=____________cm.
10.如图,河流两岸a,b互相平行,点 A,B是河岸a上的两座建筑物,点 C,D是河岸b上的两点,A,B的距离约为200米.某人在河岸b上的点 P 处测得∠APC=75°, ∠BPD=30°,则河流的宽度约为__________米.
能力提升
11.如图,在 Rt△ABC中,CM平分∠ACB交 AB 于点 M,过点 M作MN∥BC 交 AC 于点 N,且 MN平分∠AMC.若AN=1,则BC的长为 ( )
A.4 B.6 C.7 D.8
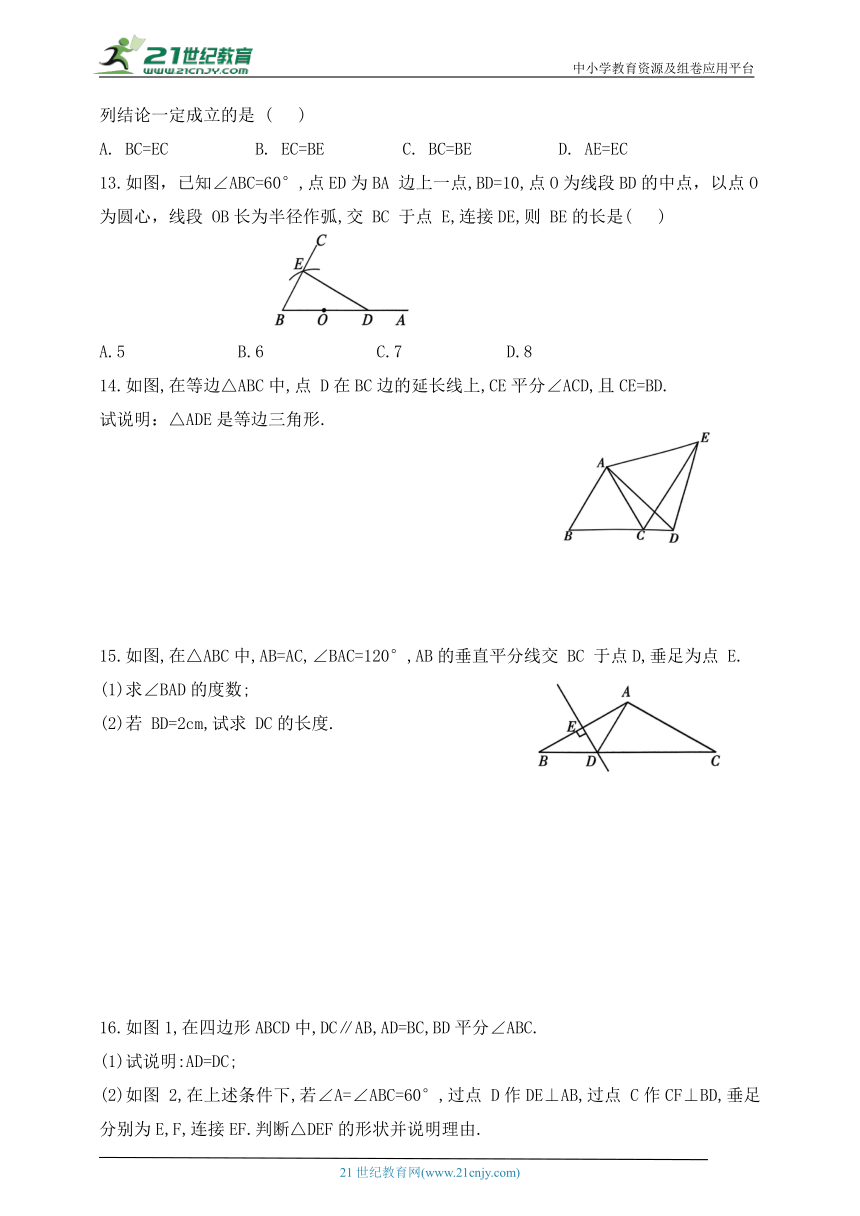
12.如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于点 D,CE平分∠ACD交 AB于点 E,则下列结论一定成立的是 ( )
A. BC=EC B. EC=BE C. BC=BE D. AE=EC
13.如图,已知∠ABC=60°,点ED为BA 边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段 OB长为半径作弧,交 BC 于点 E,连接DE,则 BE的长是( )
A.5 B.6 C.7 D.8
14.如图,在等边△ABC中,点 D在BC边的延长线上,CE平分∠ACD,且CE=BD.
试说明:△ADE是等边三角形.
15.如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交 BC 于点D,垂足为点 E.
(1)求∠BAD的度数;
(2)若 BD=2cm,试求 DC的长度.
16.如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.
(1)试说明:AD=DC;
(2)如图 2,在上述条件下,若∠A=∠ABC=60°,过点 D作DE⊥AB,过点 C作CF⊥BD,垂足分别为E,F,连接EF.判断△DEF的形状并说明理由.
核心拓展
17.如图,在等边三角形ABC中,点M为AB 边上任意一点,延长BC 至点N,使 CN=AM,连接 MN交AC 于点P,MH⊥AC于点 H.
(1)试说明:MP=NP;
(2)若AB=a,求线段 PH的长(结果用含a的代数式表示).
参考答案
1. B 2.①②③ 3.3
4.解:因为∠ABC=∠ACB,所以AB=AC.
因为点 D,E分别为边AB,AC 的中点,所以BD=CE.
在△BDC和△CEB中,因为BD=CE,∠ABC=∠ACB,BC=CB,所以△BDC≌△CEB(SAS).
所以 BE=CD.
5. D 6. C
7.解:因为CD平分∠ACB,∠ACB=120°,所以
因为AE∥DC,所以∠3=∠2=60°,∠E=∠1=60°.所以∠4=∠3=∠E=60°.
所以△ACE是等边三角形.
8. C
9.21
10.100 【解析】因为a∥b,∠APC=75°,所以∠PAB=∠APC=75°.
因为∠APC=75°,∠BPD=30°,所以∠APB=75°.所以∠APB=∠PAB,所以BP=AB=200米.
如图,过点 B作BE⊥CD于点E,则∠PEB=90°.
因为∠BPD=30°,所以 (米).故填 100.
11. B【解析】因为CM平分∠ACB,所以∠ACM=∠BCM.
因为 MN平分∠AMC,所以∠AMN=∠CMN.
因为MN∥BC,所以∠CMN=∠BCM,∠AMN=∠B.
所以∠B=∠AMN=∠CMN=∠BCM=∠ACM.所以∠B=30°=∠AMN.
在Rt△AMN中,因为AN=1,所以MN=2=NC.所以BC=2AC=2(AN+NC)=6.
12. C【解析】因为∠ACB=90°,CD⊥AB,所以∠ACD+∠BCD=90°,∠ACD+∠A=90°.
所以∠BCD=∠A.
因为CE平分∠ACD,所以∠ACE=∠DCE.
又因为∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,所以∠BEC=∠BCE.所以BC=BE.
13. A 【解析】如图,连接OE.由已知得
因为∠ABC=60°,所以△BOE是等边三角形.所以BE=OB=5.故选A.
14.解:由等边△ABC及CE平分∠ACD,可得AB=AC,∠B=∠ACE=60°.
又因为CE=BD,所以△ABD≌△ACE(SAS).所以AD=AE,∠BAD=∠CAE.
所以∠BAD-∠CAD=∠CAE-∠CAD.即∠BAC=∠DAE=60°.
又因为AD=AE,所以△ADE是等边三角形.
15.解:(1)因为 AB=AC,∠BAC=120°,所以∠B=∠C=(180°-120°)÷2=30°.
因为DE垂直平分线段AB,所以DB=DA.所以∠BAD=∠B=30°.
(2)因为AB=AC,∠BAC=120°,∠BAD=∠B=30°,所以∠DAC=∠BAC-∠BAD=90°.
又因为DB=DA,∠C=∠B=30°,所以DC=2DA=2DB=4 cm.
16.解:(1)因为 DC∥AB,所以∠CDB=∠ABD.
又因为 BD平分∠ABC,所以∠CBD=∠ABD.所以∠CDB=∠CBD,所以BC=DC.
又因为AD=BC,所以 AD=DC.
(2)△DEF为等边三角形.
理由:因为BC=DC(已证),CF⊥BD,所以点 F是BD的中点.所以
因为BD平分∠ABC,所以
因为∠DEB=90°,所以
所以△DEF为等边三角形.
17.解:(1)过点 M作MQ∥BC,交AC于点Q,如图.
在等边△ABC中,∠A=∠B=∠ACB=60°.
因为 MQ∥BC,所以∠AMQ=∠B=60°,∠AQM=∠ACB=60°,∠QMP=∠N.
所以△AMQ是等边三角形.所以AM=QM.
因为AM=CN,所以QM=CN.
在△QMP和△CNP中,所以△QMP≌△CNP(AAS).
所以 MP=NP.
(2)因为△AMQ是等边三角形,且MH⊥AC,所以AH=HQ.
因为△QMP≌△CNP,所以QP=CP.所以
因为AB=a,AB=AC,所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 轴对称
3 简单的轴对称图形
第4课时 等腰(边)三角形的判定
基础夯实
知识点一 等腰三角形的判定
1.在△ABC中,已知∠B=∠C,则( )
A. AB=BC B. AB=AC C. BC=AC D.∠A=60°
2.满足下列条件的三角形:①内角比为1:2:1;②内角比为2:2:5;③内角比为1:1:1;
④内角比为1:2:3.其中是等腰三角形的有____________.(填写序号)
3.如图,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC,则图中等腰三角形的个数是___________.
4.如图,已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB,AC的中点.试说明:BE=CD.
知识点二 等边三角形的判定
5.在△ABC中,①若AB=BC=CA,则△ABC是等边三角形;②若∠A=∠B=∠C,则△ABC为等边三角形;③有两个角都是60°的三角形是等边三角形;④一个角为60°的等腰三角形是等边三角形.上述结论中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.若一个三角形中有两个角的平分线,分别垂直于该角所对的边,则这个三角形是( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
7.如图,在△ABC中,∠ACB=120°,CD平分∠ACB,AE∥DC,交 BC的延长线于点E.试说明:△ACE是等边三角形.
知识点三 含30°角的直角三角形的性质
8.如果直角三角形的一个锐角为30°,而斜边与较短的直角边之和为18 cm,那么斜边长为( )
A.6 cm B.9 cm C.12 cm D.14 cm
9.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,AB=4 cm,则 BC=_________cm,BD=____________cm.
10.如图,河流两岸a,b互相平行,点 A,B是河岸a上的两座建筑物,点 C,D是河岸b上的两点,A,B的距离约为200米.某人在河岸b上的点 P 处测得∠APC=75°, ∠BPD=30°,则河流的宽度约为__________米.
能力提升
11.如图,在 Rt△ABC中,CM平分∠ACB交 AB 于点 M,过点 M作MN∥BC 交 AC 于点 N,且 MN平分∠AMC.若AN=1,则BC的长为 ( )
A.4 B.6 C.7 D.8
12.如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于点 D,CE平分∠ACD交 AB于点 E,则下列结论一定成立的是 ( )
A. BC=EC B. EC=BE C. BC=BE D. AE=EC
13.如图,已知∠ABC=60°,点ED为BA 边上一点,BD=10,点O为线段BD的中点,以点O为圆心,线段 OB长为半径作弧,交 BC 于点 E,连接DE,则 BE的长是( )
A.5 B.6 C.7 D.8
14.如图,在等边△ABC中,点 D在BC边的延长线上,CE平分∠ACD,且CE=BD.
试说明:△ADE是等边三角形.
15.如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交 BC 于点D,垂足为点 E.
(1)求∠BAD的度数;
(2)若 BD=2cm,试求 DC的长度.
16.如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.
(1)试说明:AD=DC;
(2)如图 2,在上述条件下,若∠A=∠ABC=60°,过点 D作DE⊥AB,过点 C作CF⊥BD,垂足分别为E,F,连接EF.判断△DEF的形状并说明理由.
核心拓展
17.如图,在等边三角形ABC中,点M为AB 边上任意一点,延长BC 至点N,使 CN=AM,连接 MN交AC 于点P,MH⊥AC于点 H.
(1)试说明:MP=NP;
(2)若AB=a,求线段 PH的长(结果用含a的代数式表示).
参考答案
1. B 2.①②③ 3.3
4.解:因为∠ABC=∠ACB,所以AB=AC.
因为点 D,E分别为边AB,AC 的中点,所以BD=CE.
在△BDC和△CEB中,因为BD=CE,∠ABC=∠ACB,BC=CB,所以△BDC≌△CEB(SAS).
所以 BE=CD.
5. D 6. C
7.解:因为CD平分∠ACB,∠ACB=120°,所以
因为AE∥DC,所以∠3=∠2=60°,∠E=∠1=60°.所以∠4=∠3=∠E=60°.
所以△ACE是等边三角形.
8. C
9.21
10.100 【解析】因为a∥b,∠APC=75°,所以∠PAB=∠APC=75°.
因为∠APC=75°,∠BPD=30°,所以∠APB=75°.所以∠APB=∠PAB,所以BP=AB=200米.
如图,过点 B作BE⊥CD于点E,则∠PEB=90°.
因为∠BPD=30°,所以 (米).故填 100.
11. B【解析】因为CM平分∠ACB,所以∠ACM=∠BCM.
因为 MN平分∠AMC,所以∠AMN=∠CMN.
因为MN∥BC,所以∠CMN=∠BCM,∠AMN=∠B.
所以∠B=∠AMN=∠CMN=∠BCM=∠ACM.所以∠B=30°=∠AMN.
在Rt△AMN中,因为AN=1,所以MN=2=NC.所以BC=2AC=2(AN+NC)=6.
12. C【解析】因为∠ACB=90°,CD⊥AB,所以∠ACD+∠BCD=90°,∠ACD+∠A=90°.
所以∠BCD=∠A.
因为CE平分∠ACD,所以∠ACE=∠DCE.
又因为∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,所以∠BEC=∠BCE.所以BC=BE.
13. A 【解析】如图,连接OE.由已知得
因为∠ABC=60°,所以△BOE是等边三角形.所以BE=OB=5.故选A.
14.解:由等边△ABC及CE平分∠ACD,可得AB=AC,∠B=∠ACE=60°.
又因为CE=BD,所以△ABD≌△ACE(SAS).所以AD=AE,∠BAD=∠CAE.
所以∠BAD-∠CAD=∠CAE-∠CAD.即∠BAC=∠DAE=60°.
又因为AD=AE,所以△ADE是等边三角形.
15.解:(1)因为 AB=AC,∠BAC=120°,所以∠B=∠C=(180°-120°)÷2=30°.
因为DE垂直平分线段AB,所以DB=DA.所以∠BAD=∠B=30°.
(2)因为AB=AC,∠BAC=120°,∠BAD=∠B=30°,所以∠DAC=∠BAC-∠BAD=90°.
又因为DB=DA,∠C=∠B=30°,所以DC=2DA=2DB=4 cm.
16.解:(1)因为 DC∥AB,所以∠CDB=∠ABD.
又因为 BD平分∠ABC,所以∠CBD=∠ABD.所以∠CDB=∠CBD,所以BC=DC.
又因为AD=BC,所以 AD=DC.
(2)△DEF为等边三角形.
理由:因为BC=DC(已证),CF⊥BD,所以点 F是BD的中点.所以
因为BD平分∠ABC,所以
因为∠DEB=90°,所以
所以△DEF为等边三角形.
17.解:(1)过点 M作MQ∥BC,交AC于点Q,如图.
在等边△ABC中,∠A=∠B=∠ACB=60°.
因为 MQ∥BC,所以∠AMQ=∠B=60°,∠AQM=∠ACB=60°,∠QMP=∠N.
所以△AMQ是等边三角形.所以AM=QM.
因为AM=CN,所以QM=CN.
在△QMP和△CNP中,所以△QMP≌△CNP(AAS).
所以 MP=NP.
(2)因为△AMQ是等边三角形,且MH⊥AC,所以AH=HQ.
因为△QMP≌△CNP,所以QP=CP.所以
因为AB=a,AB=AC,所以
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
