2.3.3 等腰(边)三角形的性质同步练习(含解析)
文档属性
| 名称 | 2.3.3 等腰(边)三角形的性质同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-25 09:19:06 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章 轴对称
3 简单的轴对称图形
第3课时 等腰(边)三角形的性质
基础夯实
知识点一 等腰三角形的性质
1.如图,在△ABC 中,AB=AC,∠A=40°,CD∥AB,则∠BCD=( )
A.40° B.50° C.60° D.70°
2.如图,在△ABC中,AB=AC,点 D为BC的中点,∠BAD=35°,则∠C的度数为__________.
3.如图,在四边形ABCD中,顶点 B,D关于直线AC 对称,已知AC=10cm,BD=8cm.则阴影部分的面积为___________cm .
4.如图,在△ABC中,AB=AC,AD是 BC边上的中线,BE⊥AC于点 E.
试说明:∠CBE=∠BAD.
知识点二 等边三角形的性质
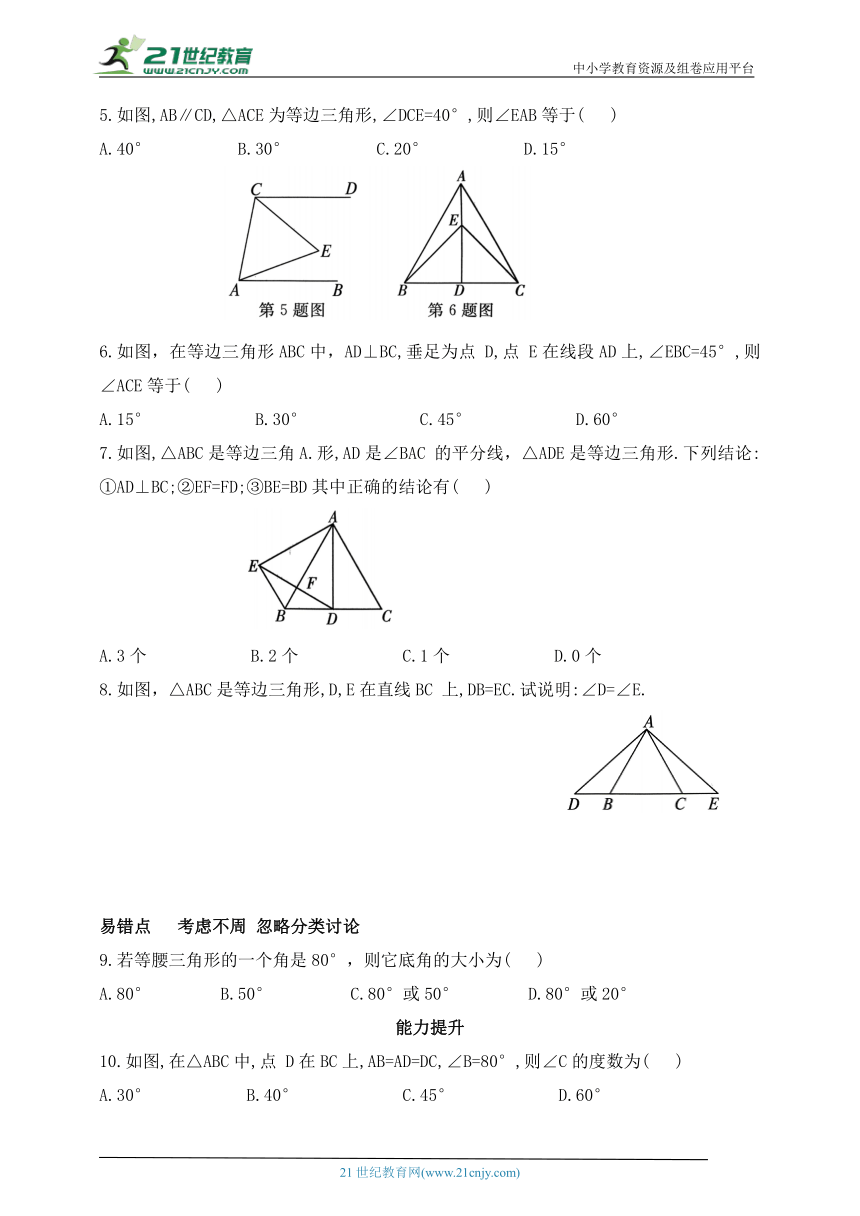
5.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
6.如图,在等边三角形ABC中,AD⊥BC,垂足为点 D,点 E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
7.如图,△ABC是等边三角A.形,AD是∠BAC 的平分线,△ADE是等边三角形.下列结论:①AD⊥BC;②EF=FD;③BE=BD其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
8.如图,△ABC是等边三角形,D,E在直线BC 上,DB=EC.试说明:∠D=∠E.
易错点 考虑不周 忽略分类讨论
9.若等腰三角形的一个角是80°,则它底角的大小为( )
A.80° B.50° C.80°或50° D.80°或20°
能力提升
10.如图,在△ABC中,点 D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
A.30° B.40° C.45° D.60°
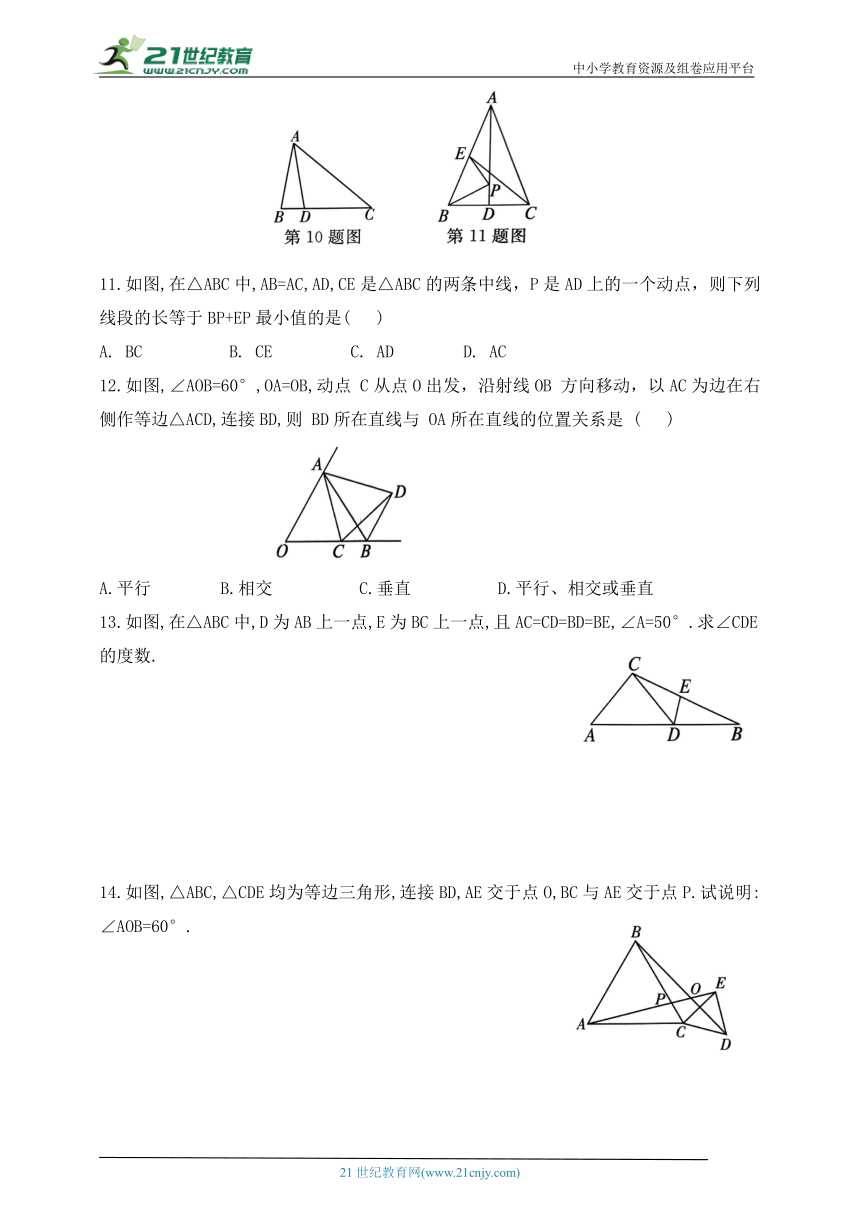
11.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于BP+EP最小值的是( )
A. BC B. CE C. AD D. AC
12.如图,∠AOB=60°,OA=OB,动点 C从点O出发,沿射线OB 方向移动,以AC为边在右侧作等边△ACD,连接BD,则 BD所在直线与 OA所在直线的位置关系是 ( )
A.平行 B.相交 C.垂直 D.平行、相交或垂直
13.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°.求∠CDE的度数.
14.如图,△ABC,△CDE均为等边三角形,连接BD,AE交于点O,BC与AE交于点P.试说明:∠AOB=60°.
15.如图,已知AB=AC=AD,且AD∥BC.试说明:∠C=2∠D.
16.如图,点 E,F分别是等边三角形ABC的边AB,AC上的点,且 BE=AF,CE与BF相交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
核心拓展
17.已知:线段 AB⊥直线 l于点 B,点 D在直线上,分别以AB,AD为边作等边△ABC和△ADE,直线CE交直线于点F.
(1)当点 F在线段BD上时,如图1,试说明:DF=CE-CF;
(2)当点 F在线段BD延长线上时,如图2;当点F在线段 DB延长线上时,如图3.请分别写出线段 DF,CE, CF之间的数量关系,不需要说明理由;
(3)在(1)(2)的条件下,若 BD=2BF,EF=6,则CF=____________.
参考答案
1. D 【解析】因为在△ABC中,AB=AC,∠A=40°,所以∠ABC=∠ACB=70°.
因为CD∥AB,所以∠BCD=∠ABC=70°.故选D.
2.55°
3.20【解析】因为顶点 B,D关于直线AC 对称,所以AC⊥BD,BE=DE,所以阴影部分的面积为四边形 ABCD面积的一半.所以阴影部分的面积
4.解:因为AB=AC,所以△ABC是等腰三角形.
因为AD是BC边上的中线,所以AD⊥BC,∠BAD=∠CAD.所以∠CAD+∠C=90°.
因为BE⊥AC,所以∠CBE+∠C=90°.所以∠CBE=∠CAD.所以∠CBE=∠BAD.
5. C【解析】因为AB∥CD,所以∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°.因为△ACE为等边三角形,所以∠ECA=∠EAC=60°.所以∠EAB=180°-40°-60°-60°=20°.故选C.
6. A 7. A
8.解:因为△ABC是等边三角形,所以AB=AC,∠ABC=∠ACB=60°.
所以∠ABD=∠ACE=120°.
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS).所以∠D=∠E.
9. C【解析】已知80°的角可做底角,也可做顶角,易漏掉80°的角作底角这一情况,而错选B.
10. B
11. B【解析】由AB=AC,可得△ABC是等腰三角形,根据等腰三角形的“三线合一”性质可知点B与点C关于直线AD对称,BP=CP,因此EP+CP的最小值为CE的长,即BP+EP的最小值为CE的长.
12. A【解析】易得△AOC≌△ABD,所以∠ABD=∠AOC=60°.从而易得BD∥OA.
13.解:因为AC=CD,所以∠ADC=∠A=50°.又因为CD=BD,所以∠B=∠BCD.
因为∠ADC=∠B+∠BCD,所以∠B=25°.
因为 BD=BE,所以 77.5°.
因为∠ADC +∠CDE+∠BDE=180°,所以∠CDE=52.5°.
14.解:因为△ABC,△CDE均为等边三角形,
所以AC=BC,CE=CD,∠ACB=∠DCE=60°,所以∠ACE=∠BCD.
在△ACE和△BCD中,因为AC=BC,∠ACE=∠BCD,CE=CD,所以△ACE≌△BCD(SAS).
所以∠CAE=∠CBD.
在△APC和△BPO中,又因为∠APC=∠BPO,所以∠AOB=∠ACB=60°.
15.解:因为AB=AC=AD,所以∠ABC=∠C,∠ABD=∠D.
因为AD∥BC,所以∠CBD=∠D.所以∠ABD+∠CBD=2∠D,即∠ABC=2∠D.
所以∠C=2∠D.
16.解:(1)因为△ABC是等边三角形,所以AB=BC,∠A=∠EBC.
又因为BE=AF,所以△BCE≌△ABF(SAS).所以CE=BF.
(2)由(1)得△BCE≌△ABF,所以∠PCB=∠ABF.
所以∠PCB+∠PBC=∠ABF+∠PBC=∠EBC=60°.
因为∠BPC+∠PCB+∠PBC=180°,所以∠BPC=180°-(∠PCB+∠PBC)=180°-60°=120°.
17.解:(1)因为△ABC,△ADE是等边三角形,所以AB=AC,AD=AE,∠BAC=∠DAE=60°.
所以∠BAD=∠CAE.所以△BAD≌△CAE(SAS).所以BD=CE,∠ACE=∠ABD=90°.
所以∠FCB=180°-∠BCA-∠ACE=30°.
因为∠DBC=∠DBA-∠CBA=30°,所以∠DBC=∠FCB.所以CF=BF.
所以DF=DB-FB=CE-CF.
(2)当点 F在线段BD延长线上时,DF=CF-CE;
当点 F在线段DB 延长线上时,DF=CE+CF.
(3)如图1,CF=2;如图2,不成立;如图 3,CF=6.
综上,CF=2或6,故填 2或6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 轴对称
3 简单的轴对称图形
第3课时 等腰(边)三角形的性质
基础夯实
知识点一 等腰三角形的性质
1.如图,在△ABC 中,AB=AC,∠A=40°,CD∥AB,则∠BCD=( )
A.40° B.50° C.60° D.70°
2.如图,在△ABC中,AB=AC,点 D为BC的中点,∠BAD=35°,则∠C的度数为__________.
3.如图,在四边形ABCD中,顶点 B,D关于直线AC 对称,已知AC=10cm,BD=8cm.则阴影部分的面积为___________cm .
4.如图,在△ABC中,AB=AC,AD是 BC边上的中线,BE⊥AC于点 E.
试说明:∠CBE=∠BAD.
知识点二 等边三角形的性质
5.如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A.40° B.30° C.20° D.15°
6.如图,在等边三角形ABC中,AD⊥BC,垂足为点 D,点 E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
7.如图,△ABC是等边三角A.形,AD是∠BAC 的平分线,△ADE是等边三角形.下列结论:①AD⊥BC;②EF=FD;③BE=BD其中正确的结论有( )
A.3个 B.2个 C.1个 D.0个
8.如图,△ABC是等边三角形,D,E在直线BC 上,DB=EC.试说明:∠D=∠E.
易错点 考虑不周 忽略分类讨论
9.若等腰三角形的一个角是80°,则它底角的大小为( )
A.80° B.50° C.80°或50° D.80°或20°
能力提升
10.如图,在△ABC中,点 D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )
A.30° B.40° C.45° D.60°
11.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD上的一个动点,则下列线段的长等于BP+EP最小值的是( )
A. BC B. CE C. AD D. AC
12.如图,∠AOB=60°,OA=OB,动点 C从点O出发,沿射线OB 方向移动,以AC为边在右侧作等边△ACD,连接BD,则 BD所在直线与 OA所在直线的位置关系是 ( )
A.平行 B.相交 C.垂直 D.平行、相交或垂直
13.如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°.求∠CDE的度数.
14.如图,△ABC,△CDE均为等边三角形,连接BD,AE交于点O,BC与AE交于点P.试说明:∠AOB=60°.
15.如图,已知AB=AC=AD,且AD∥BC.试说明:∠C=2∠D.
16.如图,点 E,F分别是等边三角形ABC的边AB,AC上的点,且 BE=AF,CE与BF相交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
核心拓展
17.已知:线段 AB⊥直线 l于点 B,点 D在直线上,分别以AB,AD为边作等边△ABC和△ADE,直线CE交直线于点F.
(1)当点 F在线段BD上时,如图1,试说明:DF=CE-CF;
(2)当点 F在线段BD延长线上时,如图2;当点F在线段 DB延长线上时,如图3.请分别写出线段 DF,CE, CF之间的数量关系,不需要说明理由;
(3)在(1)(2)的条件下,若 BD=2BF,EF=6,则CF=____________.
参考答案
1. D 【解析】因为在△ABC中,AB=AC,∠A=40°,所以∠ABC=∠ACB=70°.
因为CD∥AB,所以∠BCD=∠ABC=70°.故选D.
2.55°
3.20【解析】因为顶点 B,D关于直线AC 对称,所以AC⊥BD,BE=DE,所以阴影部分的面积为四边形 ABCD面积的一半.所以阴影部分的面积
4.解:因为AB=AC,所以△ABC是等腰三角形.
因为AD是BC边上的中线,所以AD⊥BC,∠BAD=∠CAD.所以∠CAD+∠C=90°.
因为BE⊥AC,所以∠CBE+∠C=90°.所以∠CBE=∠CAD.所以∠CBE=∠BAD.
5. C【解析】因为AB∥CD,所以∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°.因为△ACE为等边三角形,所以∠ECA=∠EAC=60°.所以∠EAB=180°-40°-60°-60°=20°.故选C.
6. A 7. A
8.解:因为△ABC是等边三角形,所以AB=AC,∠ABC=∠ACB=60°.
所以∠ABD=∠ACE=120°.
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS).所以∠D=∠E.
9. C【解析】已知80°的角可做底角,也可做顶角,易漏掉80°的角作底角这一情况,而错选B.
10. B
11. B【解析】由AB=AC,可得△ABC是等腰三角形,根据等腰三角形的“三线合一”性质可知点B与点C关于直线AD对称,BP=CP,因此EP+CP的最小值为CE的长,即BP+EP的最小值为CE的长.
12. A【解析】易得△AOC≌△ABD,所以∠ABD=∠AOC=60°.从而易得BD∥OA.
13.解:因为AC=CD,所以∠ADC=∠A=50°.又因为CD=BD,所以∠B=∠BCD.
因为∠ADC=∠B+∠BCD,所以∠B=25°.
因为 BD=BE,所以 77.5°.
因为∠ADC +∠CDE+∠BDE=180°,所以∠CDE=52.5°.
14.解:因为△ABC,△CDE均为等边三角形,
所以AC=BC,CE=CD,∠ACB=∠DCE=60°,所以∠ACE=∠BCD.
在△ACE和△BCD中,因为AC=BC,∠ACE=∠BCD,CE=CD,所以△ACE≌△BCD(SAS).
所以∠CAE=∠CBD.
在△APC和△BPO中,又因为∠APC=∠BPO,所以∠AOB=∠ACB=60°.
15.解:因为AB=AC=AD,所以∠ABC=∠C,∠ABD=∠D.
因为AD∥BC,所以∠CBD=∠D.所以∠ABD+∠CBD=2∠D,即∠ABC=2∠D.
所以∠C=2∠D.
16.解:(1)因为△ABC是等边三角形,所以AB=BC,∠A=∠EBC.
又因为BE=AF,所以△BCE≌△ABF(SAS).所以CE=BF.
(2)由(1)得△BCE≌△ABF,所以∠PCB=∠ABF.
所以∠PCB+∠PBC=∠ABF+∠PBC=∠EBC=60°.
因为∠BPC+∠PCB+∠PBC=180°,所以∠BPC=180°-(∠PCB+∠PBC)=180°-60°=120°.
17.解:(1)因为△ABC,△ADE是等边三角形,所以AB=AC,AD=AE,∠BAC=∠DAE=60°.
所以∠BAD=∠CAE.所以△BAD≌△CAE(SAS).所以BD=CE,∠ACE=∠ABD=90°.
所以∠FCB=180°-∠BCA-∠ACE=30°.
因为∠DBC=∠DBA-∠CBA=30°,所以∠DBC=∠FCB.所以CF=BF.
所以DF=DB-FB=CE-CF.
(2)当点 F在线段BD延长线上时,DF=CF-CE;
当点 F在线段DB 延长线上时,DF=CE+CF.
(3)如图1,CF=2;如图2,不成立;如图 3,CF=6.
综上,CF=2或6,故填 2或6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
